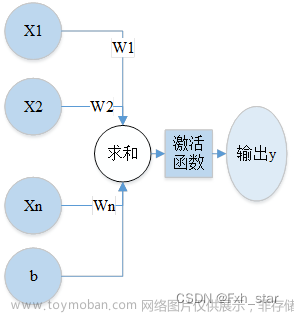
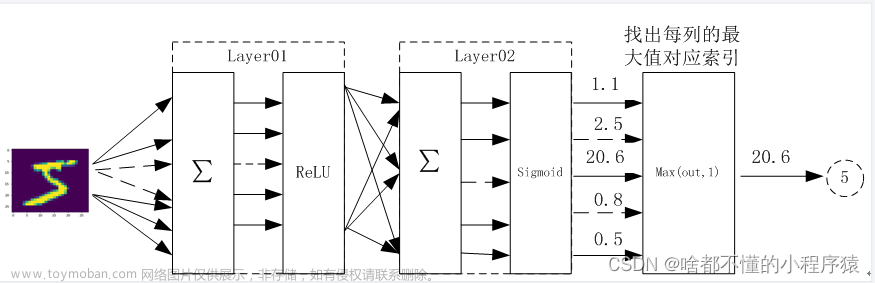
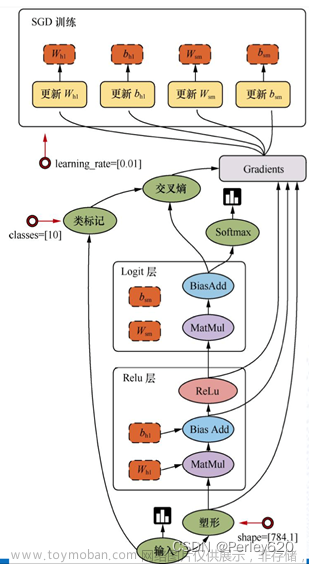
一、前向传播
作用于每一层的输入，通过逐层计算得到输出结果
二、反向传播
作用于网络输出，通过计算梯度由深到浅更新网络参数
三、整体架构
层次结构：逐层变换数据
神经元：数据量、矩阵大小（代表输入特征的数量）
x
：
[
1
,
3
]
x：[1,3]
x：[1,3]
w
1
：
[
3
,
4
]
w_1：[3,4]
w1：[3,4]
h
i
d
d
e
n
l
a
y
e
r
1
：
[
1
,
4
]
hidden layer1：[1,4]
hiddenlayer1：[1,4]
w
2
：
[
4
,
4
]
w_2：[4,4]
w2：[4,4]
h
i
d
d
e
n
l
a
y
e
r
2
：
[
1
,
4
]
hidden layer2：[1,4]
hiddenlayer2：[1,4]
w
3
：
[
4
,
1
]
w_3：[4,1]
w3：[4,1]
非线性操作加在每一步矩阵计算之后，增加神经网络的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。
四、神经元个数对结果的影响（Stanford例子）
Stanford可视化的神经网络，可以自行调参数试试
1、 num_neurons:1
将神经元设置为1，查看效果
layer_defs = [];
layer_defs.push({type:'input', out_sx:1, out_sy:1, out_depth:2});
layer_defs.push({type:'fc', num_neurons:1, activation: 'tanh'});
layer_defs.push({type:'fc', num_neurons:1, activation: 'tanh'});
layer_defs.push({type:'softmax', num_classes:2});
net = new convnetjs.Net();
net.makeLayers(layer_defs);
trainer = new convnetjs.SGDTrainer(net, {learning_rate:0.01, momentum:0.1, batch_size:10, l2_decay:0.001});
查看circle data，可以看出效果不佳，看上去像切了一刀。
2、 num_neurons:2
将神经元设置为2，查看效果
layer_defs = [];
layer_defs.push({type:'input', out_sx:1, out_sy:1, out_depth:2});
layer_defs.push({type:'fc', num_neurons:2, activation: 'tanh'});
layer_defs.push({type:'fc', num_neurons:2, activation: 'tanh'});
layer_defs.push({type:'softmax', num_classes:2});
net = new convnetjs.Net();
net.makeLayers(layer_defs);
trainer = new convnetjs.SGDTrainer(net, {learning_rate:0.01, momentum:0.1, batch_size:10, l2_decay:0.001});
查看circle data，可以看出效果一般，看上去像切了两刀，抛物线状。
3、 num_neurons:3
将神经元设置为3，查看效果
layer_defs = [];
layer_defs.push({type:'input', out_sx:1, out_sy:1, out_depth:2});
layer_defs.push({type:'fc', num_neurons:3, activation: 'tanh'});
layer_defs.push({type:'fc', num_neurons:3, activation: 'tanh'});
layer_defs.push({type:'softmax', num_classes:2});
net = new convnetjs.Net();
net.makeLayers(layer_defs);
trainer = new convnetjs.SGDTrainer(net, {learning_rate:0.01, momentum:0.1, batch_size:10, l2_decay:0.001});
查看circle data，可以看出效果较好。
五、正则化
正则化
R
(
w
)
R(w)
R(w)的作用：稳定时出现平滑边界
六、参数个数对结果的影响
七、激活函数
S
i
g
m
i
o
d
Sigmiod
Sigmiod：数值较大或较小时，梯度约为0，出现梯度消失问题
R
e
l
u
Relu
Relu：当前主要使用的激活函数
八、数据预处理
九、参数初始化
通常我们都使用随机策略来进行参数初始化文章来源：https://www.toymoban.com/news/detail-615737.html
十、DROP-OUT（传说中的七伤拳）
过拟合是神经网络非常头疼的一个问题！
左图是全连接神经网络，右图在神经网络训练过程中，每一层随机杀死部分神经元。DROP-OUT是防止神经网络过于复杂，进行随机杀死神经元的一种方法。
文章来源地址https://www.toymoban.com/news/detail-615737.html
到了这里，关于深度学习入门（二）：神经网络整体架构的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
