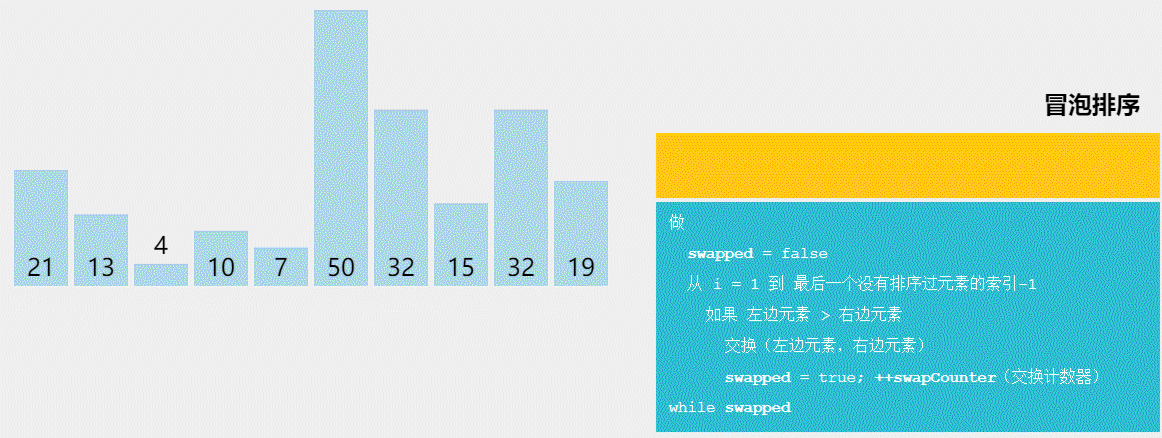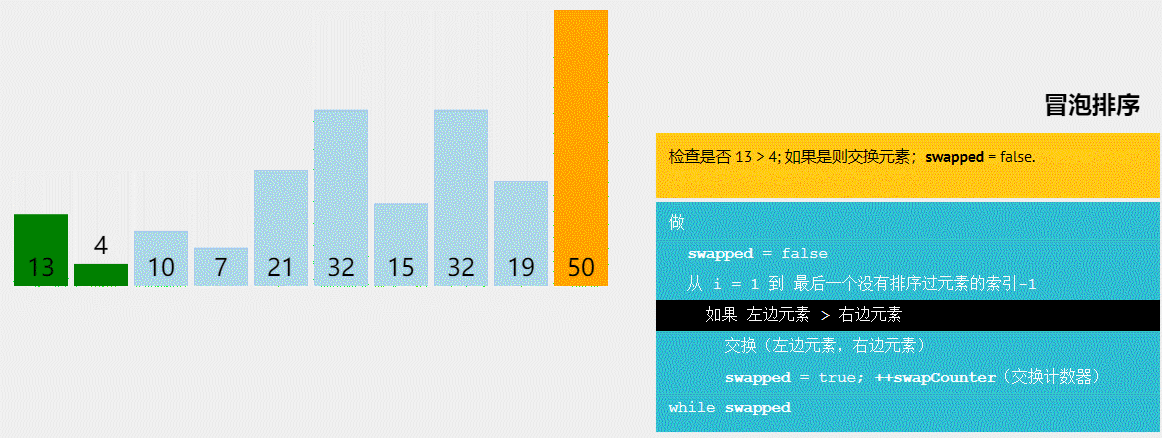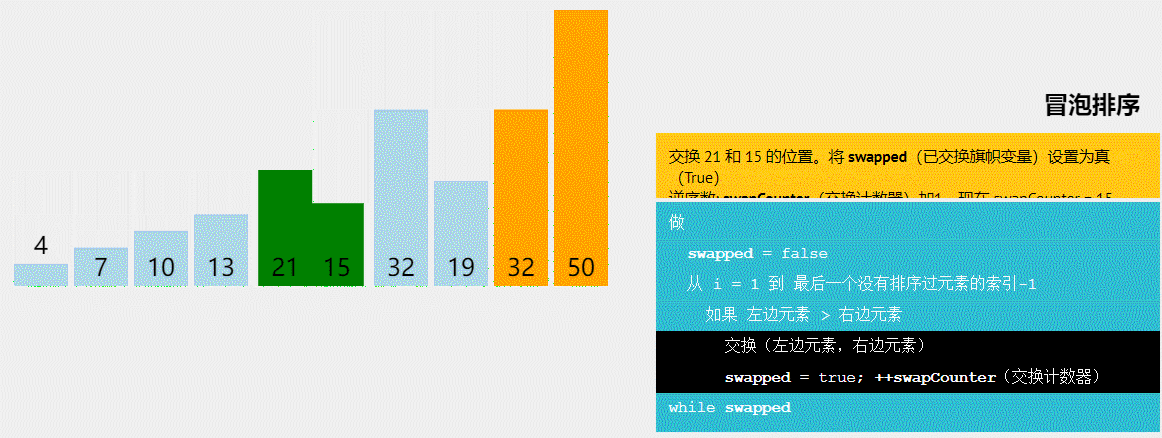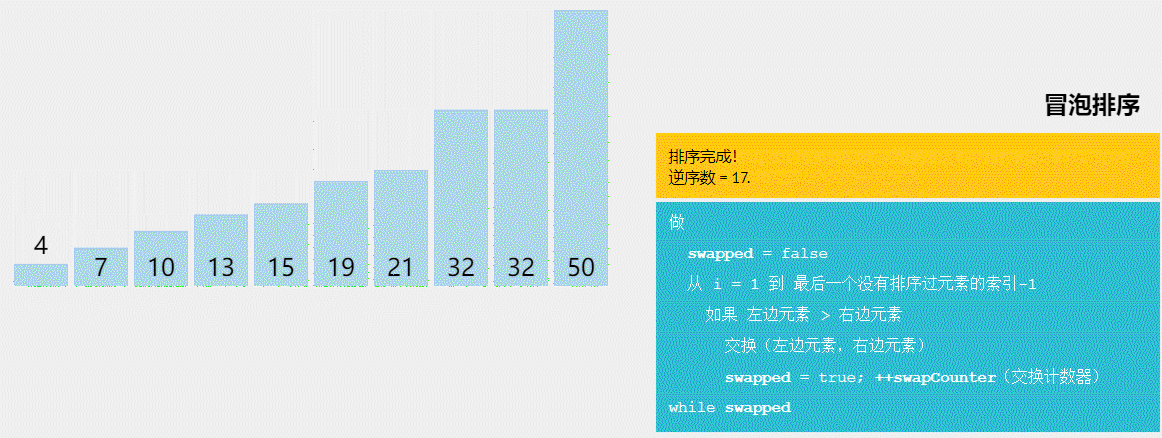数据结构基础之排序算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构基础之排序算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

在数据结构中，常见的排序算法有以下几种：

冒泡排序（Bubble Sort）：通过比较相邻元素并交换它们的位置，每轮将最大（或最小）的元素冒泡到末尾，重复执行直到排序完成。

function bubbleSort(arr) {
  const n = arr.length;
  for (let i = 0; i < n - 1; i++) {
    for (let j = 0; j < n - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
}

const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(bubbleSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]

特点：简单易懂，但对于大型数据集效率较低。
时间复杂度：
最优情况：O(n)（当数组已经排序好时）。
平均情况：O(n^2)。
最坏情况：O(n^2)。

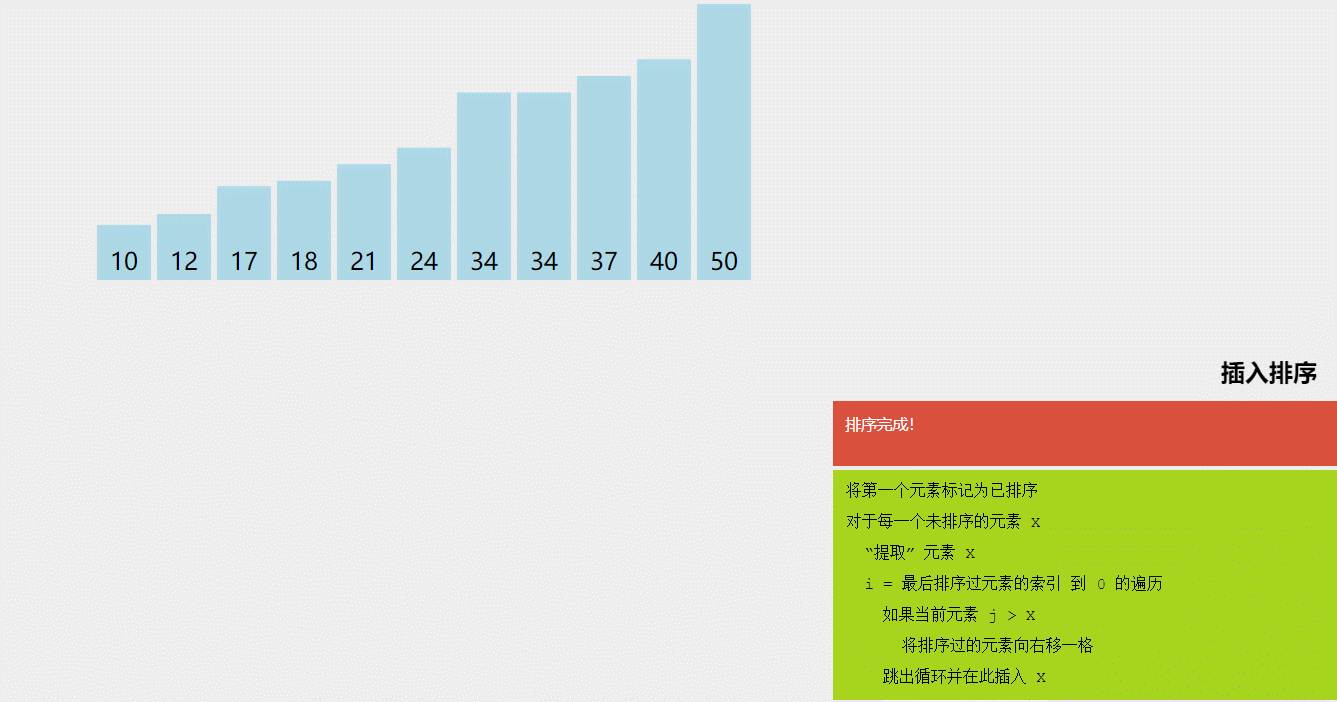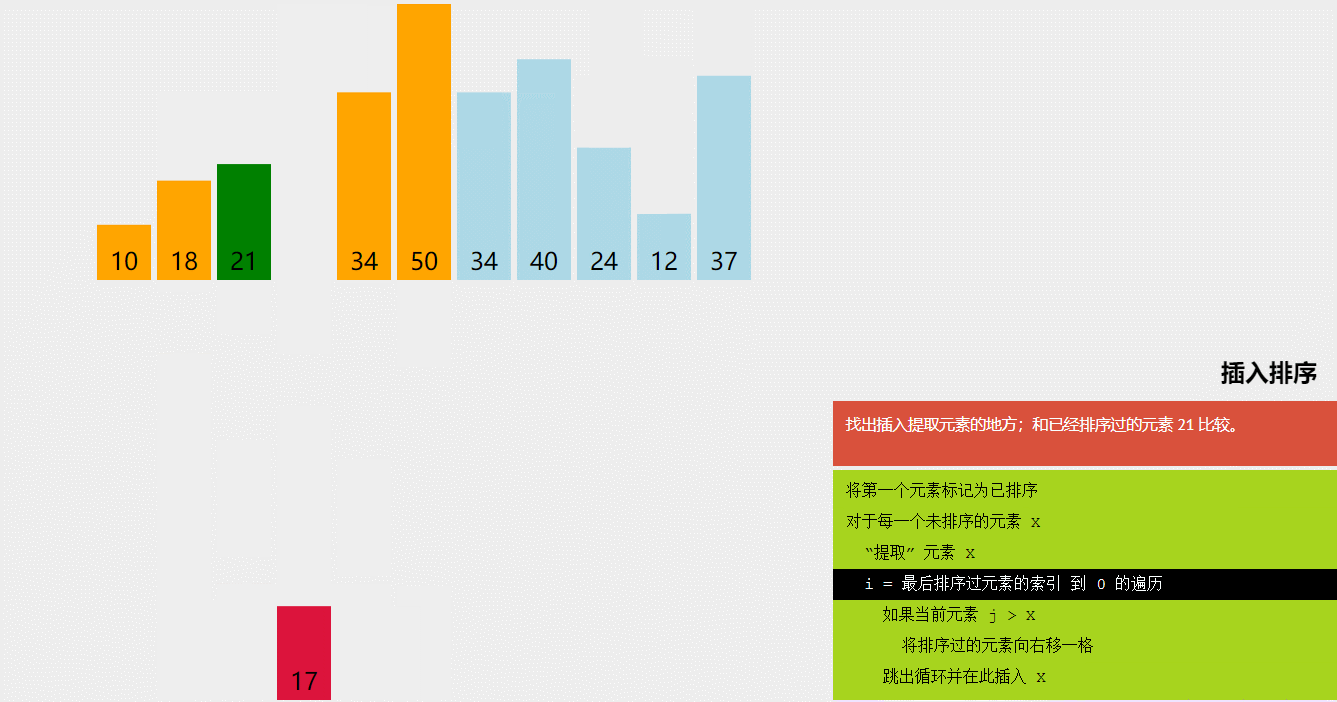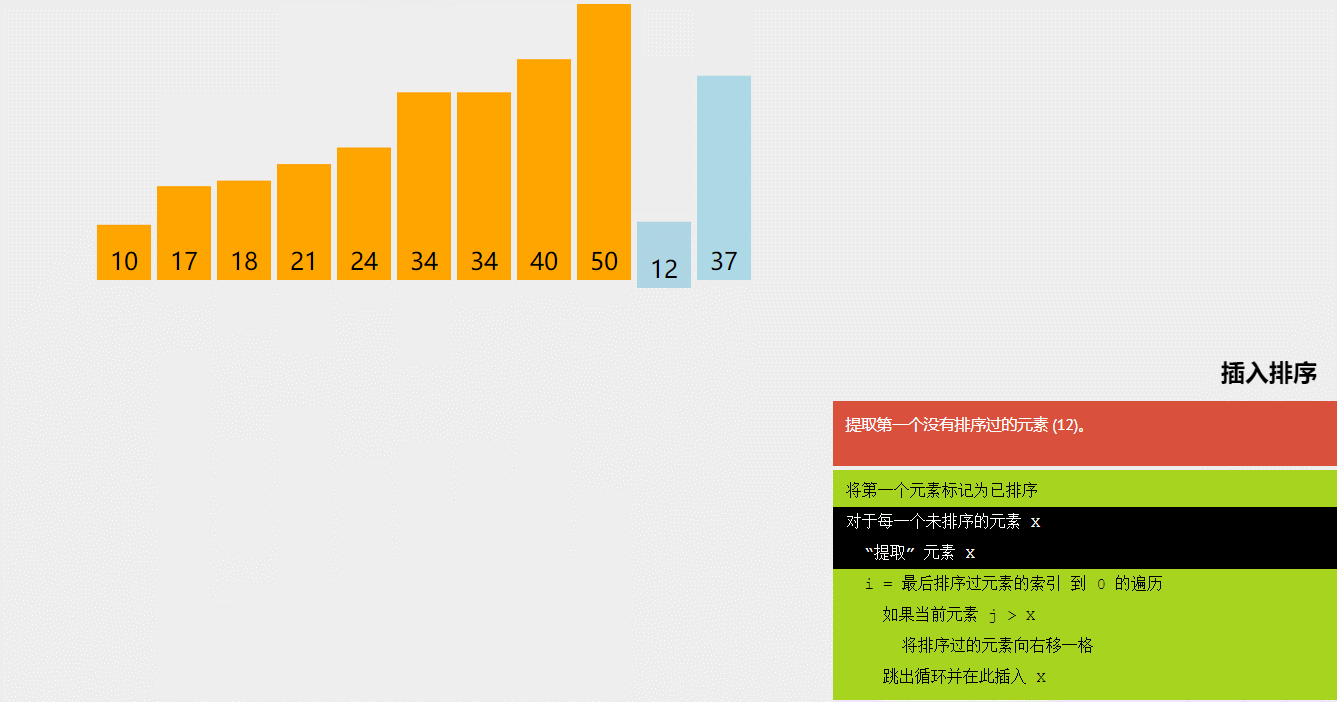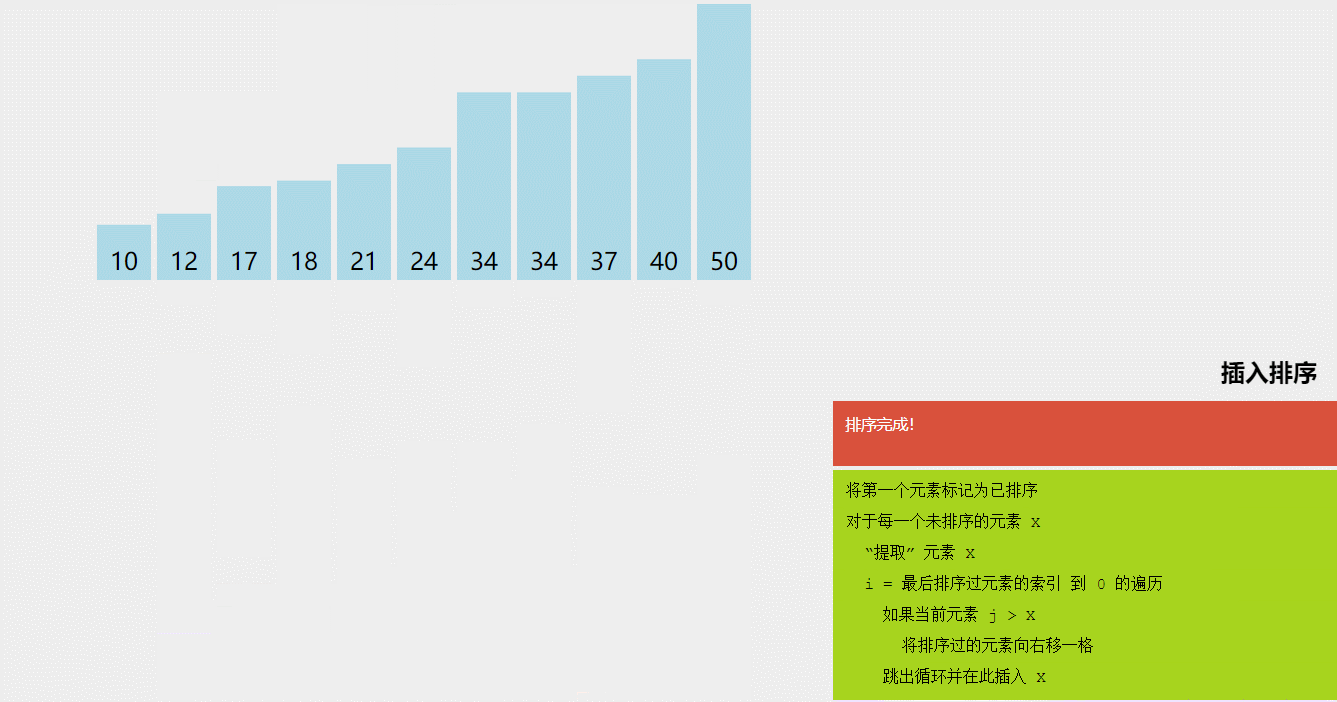
插入排序（Insertion Sort）：将数组分为已排序和未排序两部分，每次从未排序部分选择一个元素插入到已排序部分的正确位置，重复执行直到排序完成。

function insertionSort(arr) {
  const n = arr.length;
  for (let i = 1; i < n; i++) {
    let key = arr[i];
    let j = i - 1;
    while (j >= 0 && arr[j] > key) {
      arr[j + 1] = arr[j];
      j--;
    }
    arr[j + 1] = key;
  }
  return arr;
}

const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(insertionSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]

特点：适用于小型数据集和部分有序数组。
时间复杂度：
最优情况：O(n)（当数组已经排序好时）。
平均情况：O(n^2)。
最坏情况：O(n^2)。

选择排序（Selection Sort）：每轮从未排序部分选择最小（或最大）的元素，将其与未排序部分的首元素交换，重复执行直到排序完成。

function selectionSort(arr) {
  const n = arr.length;
  for (let i = 0; i < n - 1; i++) {
    let minIdx = i;
    for (let j = i + 1; j < n; j++) {
      if (arr[j] < arr[minIdx]) {
        minIdx = j;
      }
    }
    [arr[i], arr[minIdx]] = [arr[minIdx], arr[i]];
  }
  return arr;
}

const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(selectionSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]

特点：简单易懂，但对于大型数据集效率较低。
时间复杂度：
最优情况：O(n^2)。
平均情况：O(n^2)。
最坏情况：O(n^2)。

快速排序（Quick Sort）：通过选取一个基准元素，将数组分成比基准元素小和大的两部分，然后递归地对两部分进行排序。

function quickSort(arr) {
  if (arr.length <= 1) return arr;
  const pivot = arr[0];
  const left = [];
  const right = [];
  for (let i = 1; i < arr.length; i++) {
    if (arr[i] < pivot) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return [...quickSort(left), pivot, ...quickSort(right)];
}

const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(quickSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]

特点：高效且被广泛使用的排序算法。
时间复杂度：
最优情况：O(n log n)。
平均情况：O(n log n)。
最坏情况：O(n^2)。

归并排序（Merge Sort）：将数组不断分割成较小的子数组，然后再将子数组按顺序合并，重复执行直到排序完成。

function mergeSort(arr) {
  if (arr.length <= 1) return arr;
  const mid = Math.floor(arr.length / 2);
  const left = mergeSort(arr.slice(0, mid));
  const right = mergeSort(arr.slice(mid));
  return merge(left, right);
}

function merge(left, right) {
  const mergedArr = [];
  let leftIdx = 0;
  let rightIdx = 0;
  while (leftIdx < left.length && rightIdx < right.length) {
    if (left[leftIdx] < right[rightIdx]) {
      mergedArr.push(left[leftIdx]);
      leftIdx++;
    } else {
      mergedArr.push(right[rightIdx]);
      rightIdx++;
    }
  }
  return [...mergedArr, ...left.slice(leftIdx), ...right.slice(rightIdx)];
}

const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(mergeSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]

特点：稳定的排序算法，适用于大型数据集。
时间复杂度：
最优情况：O(n log n)。
平均情况：O(n log n)。
最坏情况：O(n log n)。

堆排序（Heap Sort）：利用二叉堆（最大堆或最小堆）的特性进行排序，将堆顶元素与最后一个元素交换，然后重建堆，重复执行直到排序完成。

function heapSort(arr) {
  const n = arr.length;
  for (let i = Math.floor(n / 2) - 1; i >= 0; i--) {
    heapify(arr, n, i);
  }
  for (let i = n - 1; i >= 0; i--) {
    [arr[0], arr[i]] = [arr[i], arr[0]];
    heapify(arr, i, 0);
  }
  return arr;
}

function heapify(arr, n, i) {
  let largest = i;
  const left = 2 * i + 1;
  const right = 2 * i + 2;
  if (left < n && arr[left] > arr[largest]) {
    largest = left;
  }
  if (right < n && arr[right] > arr[largest]) {
    largest = right;
  }
  if (largest !== i) {
    [arr[i], arr[largest]] = [arr[largest], arr[i]];
    heapify(arr, n, largest);
  }
}

const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(heapSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]

特点：高效的原地排序算法。
时间复杂度：
最优情况：O(n log n)。
平均情况：O(n log n)。
最坏情况：O(n log n)。

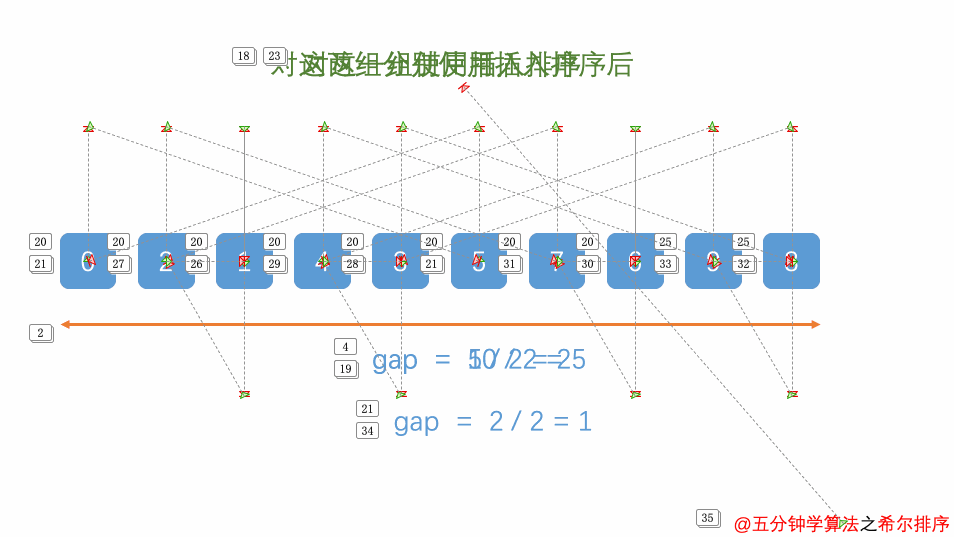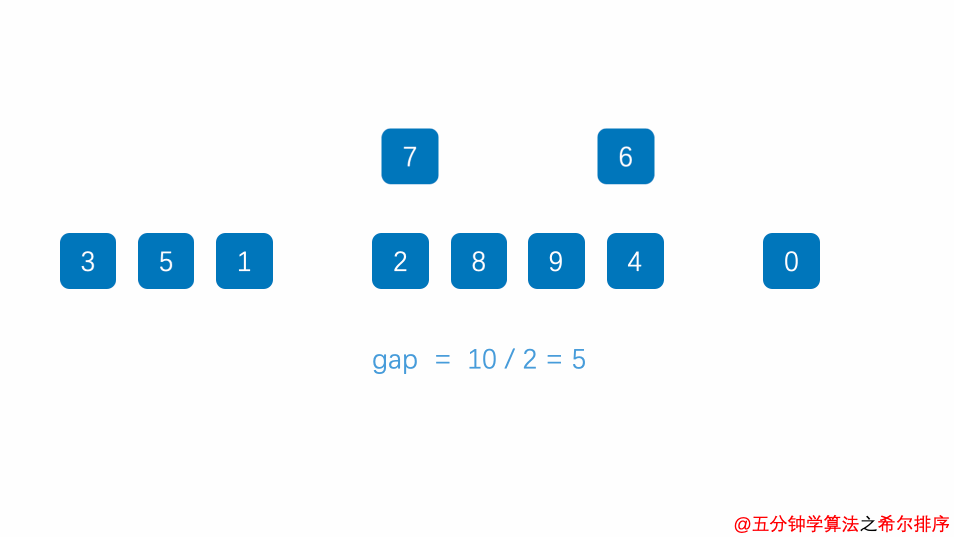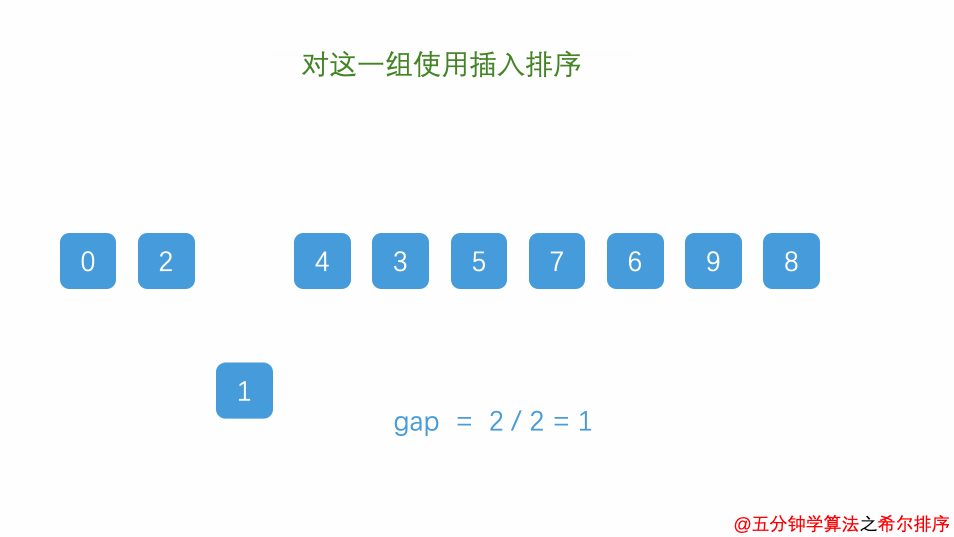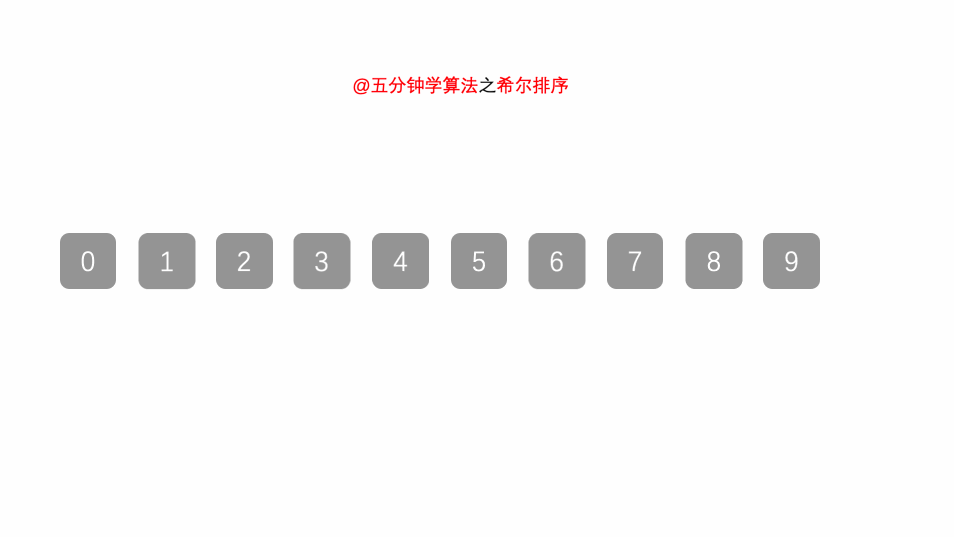
希尔排序（Shell Sort）：是插入排序的一种改进算法，通过分组进行插入排序，逐渐缩小分组间隔，直到分组间隔为1。

function shellSort(arr) {
  const n = arr.length;
  for (let gap = Math.floor(n / 2); gap > 0; gap = Math.floor(gap / 2)) {
    for (let i = gap; i < n; i++) {
      let temp = arr[i];
      let j;
      for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {
        arr[j] = arr[j - gap];
      }
      arr[j] = temp;
    }
  }
  return arr;
}

const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(shellSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]

特点：插入排序的改进版本，适用于中等大小的数据集。
时间复杂度：
最优情况：O(n log^2 n)（取决于步长序列）。
平均情况：取决于步长序列。
最坏情况：取决于步长序列。

计数排序（Counting Sort）：适用于一定范围内的整数排序，通过统计每个元素出现的次数，然后计算每个元素的位置，重复执行直到排序完成。

function countingSort(arr) {
  const n = arr.length;
  let max = Math.max(...arr);
  let min = Math.min(...arr);
  const range = max - min + 1;
  const count = Array(range).fill(0);
  const output = Array(n);

  for (let i = 0; i < n; i++) {
    count[arr[i] - min]++;
  }

  for (let i = 1; i < range; i++) {
    count[i] += count[i - 1];
  }

  for (let i = n - 1; i >= 0; i--) {
    output[count[arr[i] - min] - 1] = arr[i];
    count[arr[i] - min]--;
  }

  for (let i = 0; i < n; i++) {
    arr[i] = output[i];
  }

  return arr;
}

const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(countingSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]

特点：适用于小范围整数排序。
时间复杂度：O(n + k)，其中 n 是输入数组元素个数，k 是输入范围大小。

桶排序（Bucket Sort）：将元素根据一定规则放入不同的桶中，每个桶内部进行排序，然后按顺序合并桶内的元素，重复执行直到排序完成。

function bucketSort(arr, bucketSize = 5) {
  if (arr.length === 0) return arr;

  const max = Math.max(...arr);
  const min = Math.min(...arr);
  const bucketCount = Math.floor((max - min) / bucketSize) + 1;
  const buckets = Array(bucketCount).fill().map(() => []);

  for (let i = 0; i < arr.length; i++) {
    const bucketIndex = Math.floor((arr[i] - min) / bucketSize);
    buckets[bucketIndex].push(arr[i]);
  }

  arr.length = 0;
  for (let i = 0; i < buckets.length; i++) {
    insertionSort(buckets[i]);
    arr.push(...buckets[i]);
  }

  return arr;
}

const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(bucketSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]

特点：适用于均匀分布的数据。
时间复杂度：O(n + k)，其中 n 是输入数组元素个数，k 是桶的个数。

基数排序（Radix Sort）：按照位数将元素分配到不同的桶中，然后按顺序合并桶内的元素，重复执行直到所有位数排序完成。

function radixSort(arr) {
  const max = Math.max(...arr);
  const maxLength = String(max).length;
  let bucket = Array.from({ length: 10 }, () => []);

  for (let i = 0; i < maxLength; i++) {
    for (let j = 0; j < arr.length; j++) {
      const digit = Math.floor(arr[j] / 10 ** i) % 10;
      bucket[digit].push(arr[j]);
    }
    arr.length = 0;
    for (let k = 0; k < bucket.length; k++) {
      arr.push(...bucket[k]);
      bucket[k].length = 0;
    }
  }

  return arr;
}

const arr = [64, 34, 25, 12, 22, 11, 90];
console.log(radixSort(arr)); // Output: [11, 12, 22, 25, 34, 64, 90]