目录
插入排序
思想
算法步骤
代码
复杂度
选择排序
思想
算法步骤
代码
复杂度
堆排序
思想
算法步骤
代码
复杂度
快速排序
思想
算法步骤
代码
复杂度
稳定性
插入排序
思想
插入排序是一种简单直观的排序算法。它的工作原理是将数组分为已排序和未排序两部分,然后依次将未排序元素插入到已排序部分的正确位置,直至整个数组排序完成。
算法步骤
1.从第一个元素开始,将其视为已排序部分
2.取出下一个元素,在已排序部分从后向前进行比较,找到合适的位置并插入
3.重复上述步骤,直到所有元素都被插入到已排序部分。
代码
public static void insertSort(int[] array) {
for (int i = 1; i < array.length; i++) {
int tmp = array[i];
int j = i - 1;
for (; j >= 0; j--) {
if(tmp < array[j]) {
array[j+1] = array[j];
}else {
break;
}
}
array[j+1] = tmp;
}
}复杂度
- 最坏情况时间复杂度:O(n^2) (数组完全逆序)
- 最好情况时间复杂度:O(n) (数组已经有序)
- 平均情况时间复杂度:O(n^2)
- 空间复杂度:O(1) (原地排序)
选择排序
思想
选择排序也是一种简单的排序算法。它的主要思想是每次从未排序部分选择最小(或最大)的元素,放到已排序部分的末尾,逐步形成有序序列。
算法步骤
1.从数组中找到最小元素,将其与第一个元素交换位置,将第一个元素视为已排序部分。
2.从剩余的未排序部分中找到最小元素,将其与第二个元素交换位置,将前两个元素视为已排序部分。
3.重复上述步骤,直到所有元素都排序完成。
代码
public static void selectSort(int[] array) {
for (int i = 0; i < array.length; i++) {
int min = i;
for (int j = i+1; j < array.length; j++) {
if (array[j] < array[min]) {
min = j;
}
}
swap(array, i, min);
}
}
private static void swap(int[] array, int i, int min) {
int tmp = array[i];
array[i] = array[min];
array[min] = tmp;
}复杂度
- 最坏情况时间复杂度:O(n^2)
- 最好情况时间复杂度:O(n^2)
- 平均情况时间复杂度:O(n^2)
- 空间复杂度:O(1) (原地排序)
堆排序
思想
堆排序是一种高效的排序算法,利用了二叉堆的数据结构。它通过构建最大堆(升序排序时使用)或最小堆(降序排序时使用)来进行排序。
算法步骤
1.将输入数组构建成一个二叉堆。
2.不断从堆顶取出最大(或最小)元素,放入已排序部分的末尾,并调整堆保持其性质。
3.重复上述步骤,直到所有元素都被取出,形成有序序列。
代码
public static void heapSort(int[] array) {
createBigHeap(array);
int end = array.length - 1;
while (end > 0) {
swap(array,0,end);
siftDown(array,0,end);
end--;
}
}
private static void createBigHeap(int[] array) {
for (int parent = (array.length-1-1) / 2; parent >= 0; parent--) {
siftDown(array,parent,array.length);
}
}
private static void siftDown(int[] array, int parent, int end) {
int child = parent*2 + 1;
while (child < end) {
if(child+1 < end && array[child] < array[child+1]) {
child++;
}
if (array[child] > array[parent]){
swap(array,child,parent);
parent = child;
child = parent*2 + 1;
}else {
break;
}
}
}复杂度
- 最坏情况时间复杂度:O(n log n)
- 最好情况时间复杂度:O(n log n)
- 平均情况时间复杂度:O(n log n)
- 空间复杂度:O(1) (原地排序)
快速排序
思想
快速排序是一种常用且高效的排序算法,它采用了分治的思想。快速排序的核心在于选取一个基准元素,将数组分为左右两个子数组,使得左边的元素都小于等于基准,右边的元素都大于等于基准,然后对子数组递归地进行快速排序。
算法步骤
1.选择一个基准元素(通常为数组的第一个或最后一个元素)。
2.将数组分成两个子数组,使得左边子数组的元素都小于等于基准,右边子数组的元素都大 于等于基准。
3.对左右子数组递归地进行快速排序。
4.将左边子数组、基准元素和右边子数组合并成最终的有序数组。
代码
public static void quickSort(int[] array) {
quick(array,0,array.length-1);
}
private static void quick(int[] array, int start, int end) {
if(start >= end) {
return;
}
int pivot = partition(array,start,end);
quick(array,start,pivot-1);
quick(array,pivot+1,end);
}
//挖坑法
private static int partition(int[] array, int start, int end) {
int key = array[start];
while (start < end) {
while (start < end && array[end] >= key) {
end--;
}
array[start] = array[end];
while (start < end && array[start+1] <= key) {
start++;
}
array[end] = array[start];
}
array[start] = key;
return start;
}复杂度
- 最坏情况时间复杂度:O(n^2) (基准选取不当导致)
- 最好情况时间复杂度:O(n log n) (每次都能将数组平衡地分割)
- 平均情况时间复杂度:O(n log n)
- 空间复杂度:O(log n) (递归调用栈的深度
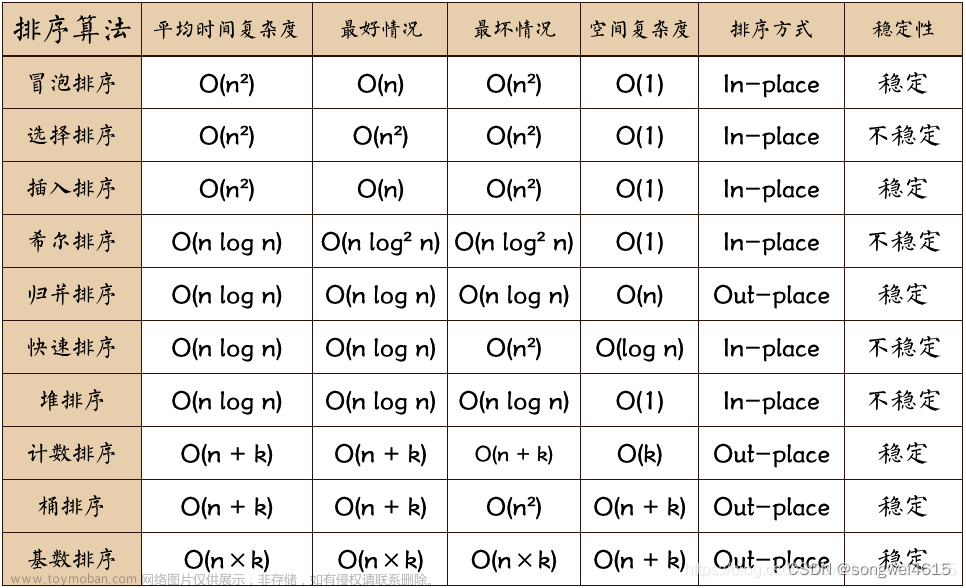
稳定性
稳定的排序:插入排序,选择排序文章来源:https://www.toymoban.com/news/detail-615900.html
不稳定排序:快速排序,堆排序文章来源地址https://www.toymoban.com/news/detail-615900.html
到了这里,关于插入,选择,堆,快速排序算法思想与复杂度的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!