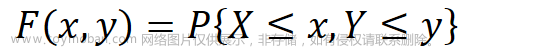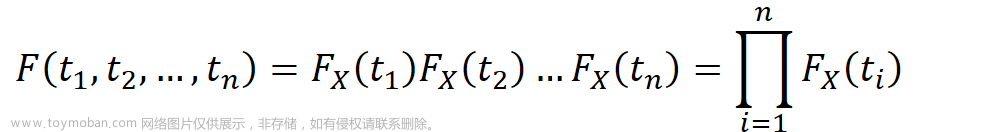负二项分布
负二项分布是伯努利分布的推广，它模拟了在指定（非随机）失败次数（表示为r）发生之前，一系列独立且同分布的伯努利试验中的成功次数
负二项分布可以用来确定一个系列中多于1次失败的概率
比如：计算一台机器彻底崩溃前的天数、输掉系列赛冠军需要进行多少场比赛
截图来源：Negative binomial distribution
方差：
Var
=
E
[
X
2
]
−
E
[
X
]
2
Var
=
∑
k
=
0
∞
k
2
(
k
+
r
−
1
k
)
p
k
(
1
−
p
)
r
−
(
r
p
1
−
p
)
2
\text{Var}=E[X^2]-E[X]^2\\ ~\\ \text{Var}=\sum_{k=0}^{\infty}k^2\begin{pmatrix}k+r-1\\k\end{pmatrix}p^k(1-p)^r-(\frac{rp}{1-p})^2\\
Var=E[X2]−E[X]2 Var=k=0∑∞k2(k+r−1k)pk(1−p)r−(1−prp)2
通过微分恒等式来计算
E
[
X
2
]
E[X^2]
E[X2]
p
2
d
d
p
1
=
p
2
d
d
p
∑
k
=
0
∞
(
k
+
r
−
1
k
)
p
k
(
1
−
p
)
r
p^2\frac{d}{dp}1=p^2\frac{d}{dp}\sum_{k=0}^{\infty}\begin{pmatrix}k+r-1\\k\end{pmatrix}p^k(1-p)^r
p2dpd1=p2dpdk=0∑∞(k+r−1k)pk(1−p)r
最后整理求得
E
[
X
2
]
=
r
p
+
r
2
p
2
(
1
−
p
)
2
Var
=
E
[
X
2
]
−
E
[
X
]
2
=
r
p
+
r
2
p
2
(
1
−
p
)
2
−
(
r
p
1
−
p
)
2
=
r
p
(
1
−
p
)
2
σ
X
2
=
r
p
(
1
−
p
)
2
E[X^2]=\frac{rp+r^2p^2}{(1-p)^2}\\ ~\\ \text{Var}=E[X^2]-E[X]^2=\frac{rp+r^2p^2}{(1-p)^2}-(\frac{rp}{1-p})^2=\frac{rp}{(1-p)^2}\\ ~\\ \sigma_X^2=\frac{rp}{(1-p)^2}
E[X2]=(1−p)2rp+r2p2 Var=E[X2]−E[X]2=(1−p)2rp+r2p2−(1−prp)2=(1−p)2rp σX2=(1−p)2rp文章来源：https://www.toymoban.com/news/detail-615919.html
例子：
文章来源地址https://www.toymoban.com/news/detail-615919.html
到了这里，关于负二项分布（一种离散分布）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
