【LeetCode 算法】Walking Robot Simulation 模拟行走机器人

这篇具有很好参考价值的文章主要介绍了【LeetCode 算法】Walking Robot Simulation 模拟行走机器人 - 哈希。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

Walking Robot Simulation 模拟行走机器人

问题描述：

机器人在一个无限大小的 XY 网格平面上行走，从点 (0, 0) 处开始出发，面向北方。该机器人可以接收以下三种类型的命令 commands ：

-2 ：向左转 90 度
-1 ：向右转 90 度
$1 <= x <= 9$ ：向前移动 x 个单位长度
在网格上有一些格子被视为障碍物 obstacles 。第 i 个障碍物位于网格点 $obstacles[i] = (x_i, y_i)$ 。

机器人无法走到障碍物上，它将会停留在障碍物的前一个网格方块上，但仍然可以继续尝试进行该路线的其余部分。

返回从原点到机器人所有经过的路径点（坐标为整数）的最大欧式距离的平方。（即，如果距离为 5 ，则返回 25 ）

$1 <= commands.length <= 10^4\\ commands[i] is one of the values in the list [-2,-1,1,2,3,4,5,6,7,8,9]\\ 0 <= obstacles.length <= 10^4\\ -3 * 10^4 <= xi, yi <= 3 * 10^4\\ 答案保证小于 2^{31}$

分析

模拟问题属于看上去很简单，但是做起来处处是坑。

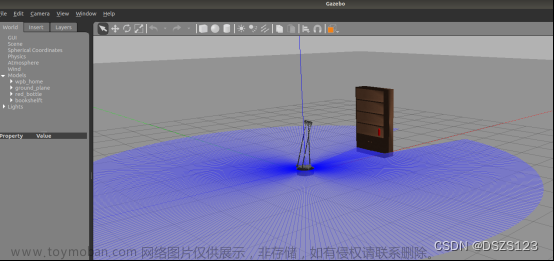
这个问题中，可以移动的范围可以看做是一个二维直角坐标系。起始点是原点[0,0],这个移动范围是不受边界限制的，它不同于一般的矩阵，有行列大小限制。

唯一受到的限制就是obstacle，而且移动的方向是4向，上下左右。

最简单的方式，就是在每次移动时确定要移动的方向，然后移动C步，每移动一步，需要判断是否遇到obstacle，如果遇到，就需要在obstacle之前停止。

如果是普通的判断坐标是否是obstacle，就需要遍历O(N)的长度，而command的次数是 $10^4$ ，所以整体来看，这个算法很可能TLE.

所以需要在某个环节进行加速，很明显只能在判断的环节，进行加速。

加速的方式有几种，目标就是缩短判断的时间复杂度，最常见的就是HashMap。

移动的过程中一定是有x或者y保持不变，

只要每次判断移动的nx,ny是否是obstacle，所以时间复杂度基本可以达到O(1).
当然预处理hashmap 的时间复杂度也大概需要 $O (N)$ ，整体的时间复杂度 $O (N + M * C)$ .

代码

哈希

public int robotSim(int[] commands, int[][] obstacles) {
        int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};
        int px = 0, py = 0, d = 1;
        Set<Integer> set = new HashSet<Integer>();
        for (int[] obstacle : obstacles) {
            set.add(obstacle[0] * 60001 + obstacle[1]);
        }
        int res = 0;
        for (int c : commands) {
            if (c < 0) {
                d += c == -1 ? 1 : -1;
                d %= 4;
                if (d < 0) {
                    d += 4;
                }
            } else {
                for (int i = 0; i < c; i++) {
                    if (set.contains((px + dirs[d][0]) * 60001 + py + dirs[d][1])) {
                        break;
                    }
                    px += dirs[d][0];
                    py += dirs[d][1];
                    res = Math.max(res, px * px + py * py);
                }
            }
        }
        return res;
    }