机器学习&&深度学习——随机梯度下降算法（及其优化）-Toy模板网

这篇具有很好参考价值的文章主要介绍了机器学习&&深度学习——随机梯度下降算法（及其优化）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

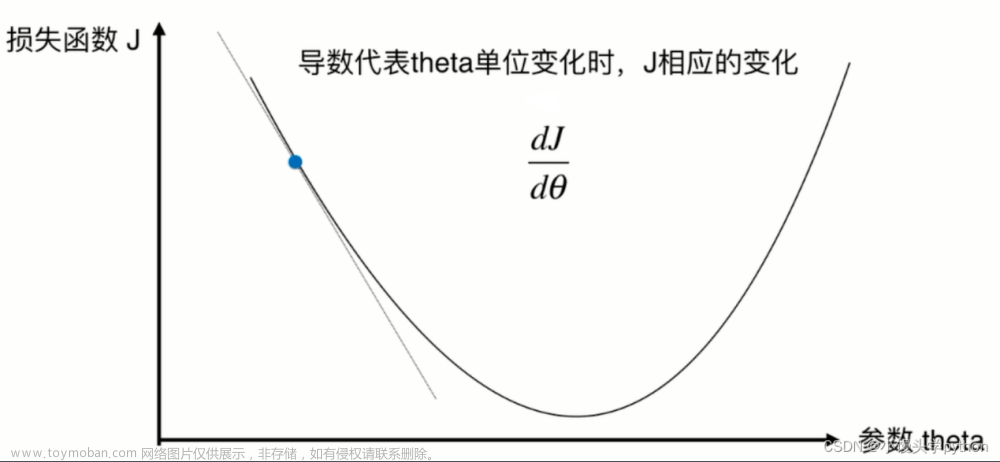
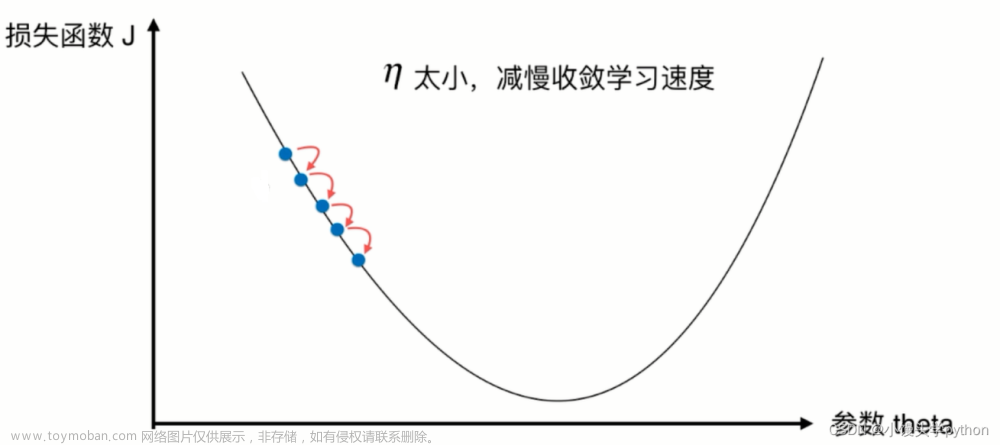
在我们没有办法得到解析解的时候，我们可以用过梯度下降来进行优化，这种方法几乎可以所有深度学习模型。
关于优化的东西，我自己曾经研究过智能排班算法和优化，所以关于如何找局部最小值，以及如何跳出局部最小值的一些基本思想是有感触的，随机梯度算法和其优化学起来倒也不难。

梯度下降法

梯度下降法是一个一阶最优化算法，通常称为最速下降法，是通过函数当前点对应梯度的反方向，使用规定步长距离进行迭代搜索，从而找到函数的一个局部最小值的算法，最好的情况是找到全局最小值。

随机梯度下降法

但是直接使用使用梯度下降法的话，每次更新参数都需要用到所有的样本，样本总量太大的话就会对算法速度影响很大，所以有了随机梯度下降算法。
它是对梯度下降算法的一种改进，且每次只随机取一部分样本进行优化，样本数量一般是2的整数次幂，取值范围32~256，以保证计算精度的同时提升计算速度，是优化深度学习网络中最常用的一类算法。
其在训练中，通常会使用一个固定的学习率进行训练，即：
$g_t=▽_{θ_{t-1}}f(θ_{t-1})\\ ▽_{θ_t}=-η*g_t\\ 其中，g_t是第t步的梯度，η是学习率$
随机梯度下降算法在优化时，完全依赖于当前batch数据得到的梯度，而学习率则是调整梯度影响大小的参数，通过控制学习率η的大小，一定程度上可以控制网络训练速度。

随机梯度下降算法的问题

随机梯度下降对大多数情况都很有效，但还存在缺陷：
1、很难确定合适的η，且所有的参数使用同样的学习率可能并不是很有效。这种情况可以采用变化学习率的训练方式，如控制网络在初期以大的学习率进行参数更新，后期以小的学习率进行参数更新（其实和遗传算法中的交叉变异概率似的，大家可以去了解自适应遗传算法的思想，道理都是一样的）
2、更容易收敛到局部最优解，而且当落入到局部最优解的时候，不容易跳出。（其实也和遗传算法可能遇到的问题类似，当时是和模拟退火算法结合了，解决了过早收敛问题，实质思想就是增大变异概率，变异了就很可能跳出局部最优了）

标准动量优化

动量通过模拟物体运动时的惯性来更新网络中的参数，即更新时在一定程度上会考虑之前参数更新的方向，同时利用当前batch计算得到的梯度，将两者结合起来计算出最终参数需要更新的大小和方向。
在优化时引入动量思想旨在加速学习，特别是面对小而连续且含有很多噪声的梯度。利用动量不仅增加了学习参数的稳定性，还会更快的学习到收敛的参数。
在引入动量后，网络的参数更新方式：
$g_t=▽_{θ_{t-1}}f(θ_{t-1})\\ m_t=μ*m_{t-1}+g_t\\ ▽_{θ_t}=-η*m_t\\ m_t为当前动量的累加\\ μ属于动量因子，用于调整上一步动量对参数的重要程度$
在网络更新初期，可利用上一次参数更新，此时下降方向一致，乘以较大的μ能够进行很好的加速；在网络更新后期，随着梯度逐渐趋于0，在局部最小值来回震荡的时候，利用动量使得更新幅度增大，跳出局部最优解的陷阱。

Nesterov动量优化

Nesterov项（Nesterov动量）是在梯度更新时做出的校正，以避免参数更新的太快，同时提高灵敏度。在动量中，之前累积的动量并不会影响当前的梯度，所以Nesterov的改进就是让之前的动量直接影响当前的动量，即：
$g_t=▽_{θ_{t-1}}f(θ_{t-1}-η*μ*m_{t-1})\\ m_t=μ*m_{t-1}+g_t\\ ▽_{θ_t}=-η*m_t$
Nesterov动量与标准动量区别在于，在当前batch梯度的计算上，Nesterov动量的梯度计算是在施加当前速度之后的梯度。所以可以看成是在标准动量的方法上添加了一个校正因子，从而提高算法更新性能。
在训练开始的时候，参数可能离最最优质的较远，需要较大学习率，经过几轮训练后，减小训练学习率 （其实就是和自适应遗传算法的思想类似）。因此也提出了很多自适应学习率的算法Adadelta、RMSProp及adam等。文章来源地址https://www.toymoban.com/news/detail-616562.html