一.冒泡排序
原理图:

实现代码:
/* 冒泡排序或者是沉底排序 */
/* int arr[]: 排序目标数组,这里元素类型以整型为例; int len: 元素个数 */
void bubbleSort (elemType arr[], int len) {
//为什么外循环小于len-1次?
//考虑临界情况,就是要循环到len-1个沉底/冒泡,则排序完毕
for (int i=0; i<len-1; i++) {
//为什么内循环小于等于len-2-i次?
//考虑临界情况,第一次循环最后是索引为len-2与len-1进行比较,所以第一次循环到len-2,
//每循环一次多沉底/冒泡一个,所以每循环完一次要多减去1,也就是多减去i,所以为len-2-i
for (int j=0; j<=len-2-i; j++) {
//相邻元素比较,符合条件进行交换,数值大的元素沉底,数值小的元素冒泡
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
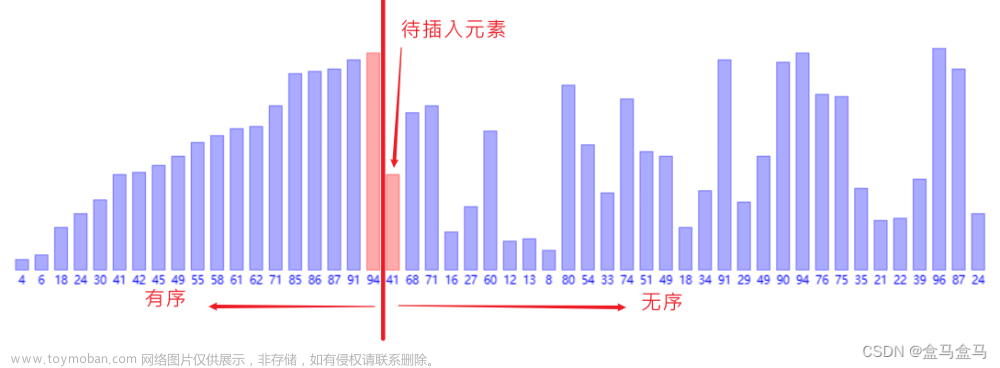
}二.插入排序
原理图:
实现代码:
// 插入排序函数(n是数组的长度)
void insertionSort(int arr[], int n) {
//先对第二个元素进行插入(索引比实际位置少一),直到对n个元素进行插入
for (int i = 1; i < n; i++) {
int key = arr[i]; // 当前要插入的元素
j = i-1;
// 将当前元素与前面的比较,将比当前元素大的元素往后移动,自己往前移动
// 直到找到合适的位置或者遍历到数组的开头
while (int j >= 0 && arr[j] > key) {
arr[j+1] = arr[j]; // 当前元素比key大,向后移动一位
j = j-1; // 继续向前比较
}
arr[j+1] = key; // 将当前元素插入到正确的位置
}
}
三.选择排序
原理图:
实现代码:
void selectionSort(int arr[], int n) {
// 遍历数组,从第一个元素到倒数第二个元素,要排序n-1次,n-1个排好才算全部排好
for (int i = 0; i < n - 1; i++) {
int minIndex = i;//假设当前循环开始时,第一个元素为最小值
// 在未排序部分寻找最小值
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j;
}
}
// 如果最小值不是当前循环的第一个元素,则进行交换
if (minIndex != i) {
// 交换两个元素的位置
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
}
上面三种简单排序算法在最坏情况及平均情况下都需要O()计算时间。
下面讨论的排序算法,它在平均情况下需要O(nlogn)时间。下面这些是目前最快的排序。
分治法:大问题分解成各个小问题,对小问题求解,使得大问题得以解决。
四.快速排序
基本思想:找到数组中的基准值,将基准值放到正确的位置,并将小于基准的元素放在基准前,大于基准的元素放在基准后。
1.普通快速排序--固定的基准值,一般以第一个元素或者最后一个元素为基准值
思路和代码如下:
简单说就是每次循环寻找数组的最后一个元素作为基准(一个概念),将这个元素放在正确的位置,并将小于基准的元素放在基准前,大于基准的元素放在基准后。【只要把小于基准的元素存到数组开头即可实现】
然后利用基准将数组划分为基准左和基准右两个子数组,递归对子数组进行此步骤。
// 交换两个元素的值
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 划分函数,选择一个元素基准元素(一般选择最后一个),将基准元素放在正确的位置
//并将将小于基准的元素放在左边,大于基准的元素放在右边
int partition(int arr[], int low, int high) {
int pivot = arr[high]; // 选择最后一个元素作为基准
int i = low;//比基准小的元素从low开始存储
for (int j = low; j < high; j++) {
//遍历数组,如果当前元素小于等于基准,交换它把数组中前面的位置进行交换
//这样保证比基准小的元素在数组的前面部分
if (arr[j] <= pivot) {
swap(&arr[i], &arr[j]);
i++;
}
}
//这样过后i的位置即为基准的位置,将基准元素放在正确的位置
swap(&arr[i], &arr[high]);
//返回基准的位置
return i;
}
// 快速排序函数
void quickSort(int arr[], int low, int high) {
if (low < high) {
// 划分数组,获取基准元素的索引
int pivotIndex = partition(arr, low, high);
// 对基准元素左右两侧的子数组进行递归排序
quickSort(arr, low, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, high);
}
}2.随机快速排序--随机的基准值
【1】为什么要用随机快速排序
普通快速排序的时候基准值总是固定在第一个或者最后一个,但是随机快速排序则是随机选择基准值。
为什么要这样呢?普通快速排序有一个问题,那就是不稳定,它的平均复杂度是nlogn,但是在某些特殊情况下可能较差,例如当数组已经有序或接近有序时,算法的时间复杂度会达到最坏情况 O(n^2)。
而采用随机快速排序可以降低最坏情况发生的概率,从而使得算法更加稳定在nlogn附近,增加算法稳定性。
【2】随机快速排序的实现
随机快速排序只要在普通快速排序的基础上再加上一个随机选取基准值即可,也就是划分函数中前加入下面这段代码:
// 随机选择基准元素
//随机生成数组的其中一个数,将其作为基准,并和原来最后一个数进行交换
//完成基准随机,其他不变即可
srand(time(NULL));
int randomIndex = low + rand() % (high - low + 1);
swap(&arr[randomIndex], &arr[high]);完整的代码:
// 交换两个元素的值
void swap(int* a, int* b) {
int temp = *a;
*a = *b;
*b = temp;
}
// 划分函数,选择一个元素基准元素(一般选择最后一个),将基准元素放在正确的位置
//并将将小于基准的元素放在左边,大于基准的元素放在右边
int partition(int arr[], int low, int high) {
// 随机选择基准元素
//随机生成数组的其中一个数,将其作为基准,并和原来最后一个数进行交换
//完成基准随机,其他不变即可
srand(time(NULL));
int randomIndex = low + rand() % (high - low + 1);
swap(&arr[randomIndex], &arr[high]);
int pivot = arr[high]; // 选择最后一个元素作为基准
int i = low;//比基准小的元素从low开始存储
for (int j = low; j < high; j++) {
//遍历数组,如果当前元素小于等于基准,交换它把数组中前面的位置进行交换
//这样保证比基准小的元素在数组的前面部分
if (arr[j] <= pivot) {
swap(&arr[i], &arr[j]);
i++;
}
}
//这样过后i的位置即为基准的位置,将基准元素放在正确的位置
swap(&arr[i], &arr[high]);
//返回基准的位置
return i;
}
// 快速排序函数
void quickSort(int arr[], int low, int high) {
if (low < high) {
// 划分数组,获取基准元素的索引
int pivotIndex = partition(arr, low, high);
// 对基准元素左右两侧的子数组进行递归排序
quickSort(arr, low, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, high);
}
} 五.归并排序/合并排序
基本思想:分治法+将两个有序序列合并成一个有序序列

怎么合并呢?
就是开辟一块临时的存储空间。就比如有两个身高从低到高的队伍,要合并成一个也是身高从小到高的队伍,就先将每个队伍的第一个人比较身高,然后低的进去,然后第二个人再与另一个队的第一个人比较身高,低的进去。。。以此类推,差不多就是这样。
下面展示的是递归版合并排序的代码:
// 合并两个有序数组
void merge(int arr[], int left, int middle, int right) {
//根据middle将数组分为两个有序数组
int i, j, k;
int n1 = middle - left + 1;
int n2 = right - middle;
// 创建临时数组
int L[n1], R[n2];
// 复制数据到临时数组 L[] 和 R[]
for (i = 0; i < n1; i++)
L[i] = arr[left + i];
for (j = 0; j < n2; j++)
R[j] = arr[middle + 1 + j];
// 合并临时数组到原数组 arr[left..right]
i = 0; // 初始化第一个子数组的索引
j = 0; // 初始化第二个子数组的索引
k = left; // 初始化合并子数组的索引
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
//如果左边队伍长一点,那L数组有剩余的元素,复制 L[] 的剩余部分
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
// 如果右边队伍长一点,那R数组有剩余的元素,复制 R[] 的剩余部分
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// 归并排序函数
void mergeSort(int arr[], int left, int right) {
if (left < right) {
// 防止溢出的写法:middle = left + (right - left) / 2;
int middle = left + (right - left) / 2;
// 递归排序左半部分和右半部分
mergeSort(arr, left, middle);
mergeSort(arr, middle + 1, right);
// 合并已排序的两部分
merge(arr, left, middle, right);
}
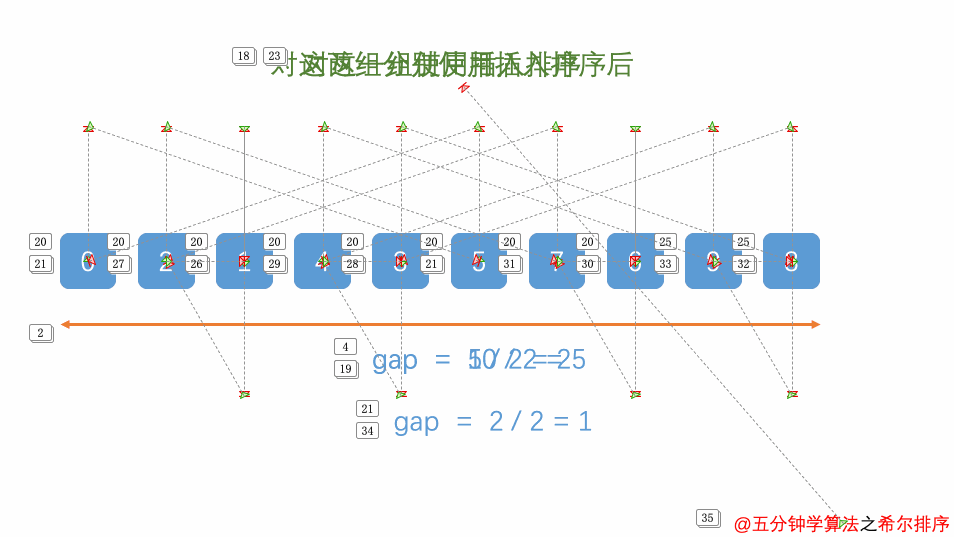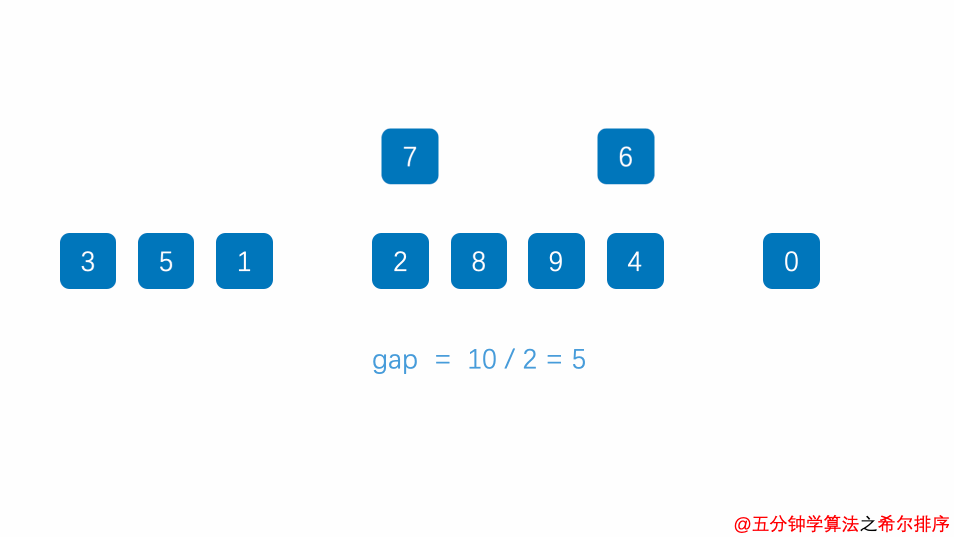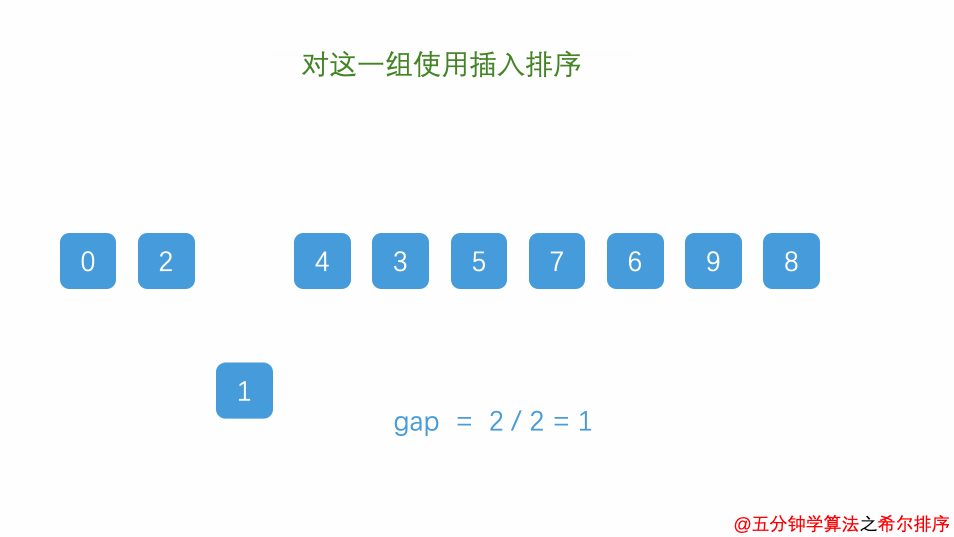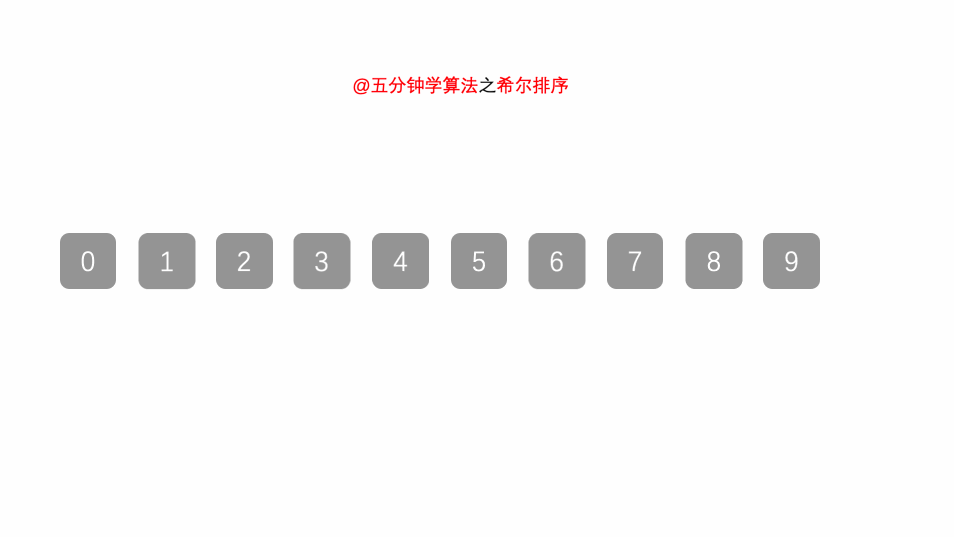
}六.希尔排序--分治法+插入排序(插入排序的提升版)
#include <stdio.h>
void shellSort(int arr[],int length) {
int increasement=length;
//确定分组的增量,你可以用你喜欢的增量,我这里取长度除以2
increasement=increasement/2;
//增量小于1停止,也就是最后对一整组进行插入排序后停止
while(increasement>1) {
//遍历每一组
for(int i=0; i<increasement; i++) {
// 对每一组进行快速排序
//遍历当前这组的元素
for(int j=i+increasement; j<length; j+=increasement) {
// 如果当前元素小于前一个元素,则进行插入操作
if(arr[j]<arr[j-increasement]) {
int temp=arr[j];
int k;
// 将大于temp的元素向后移动
for(k=j-increasement; k>=0&&temp<arr[k]; k-=increasement) {
arr[k+increasement]=arr[k];
}
// 插入temp到正确的位置
arr[k+increasement]=temp;
}
}
}
//缩小增量
increasement=increasement/2;
}
}
void printArray(int arr[], int n) {
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}
int main() {
int arr[] = {12, 34, 54, 2, 3};
int n = sizeof(arr) / sizeof(arr[0]);
printf("原始数组: ");
printArray(arr, n);
shellSort(arr, n);
printf("排序后的数组: ");
printArray(arr, n);
return 0;
}为什么分组后的插入排序会快呢?
因为插入排序在元素序列基本有序和元素个数比较小的时候速度较快,而分组就创造了这种条件。文章来源:https://www.toymoban.com/news/detail-616698.html
总结
可以发现,下面三种快的排序(平均情况下的时间复杂度都为O(nlogn))都使用了分治法,将一个大问题分为几个相同的小问题,分而治之。文章来源地址https://www.toymoban.com/news/detail-616698.html
到了这里,关于算法与数据结构(四)--排序算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!