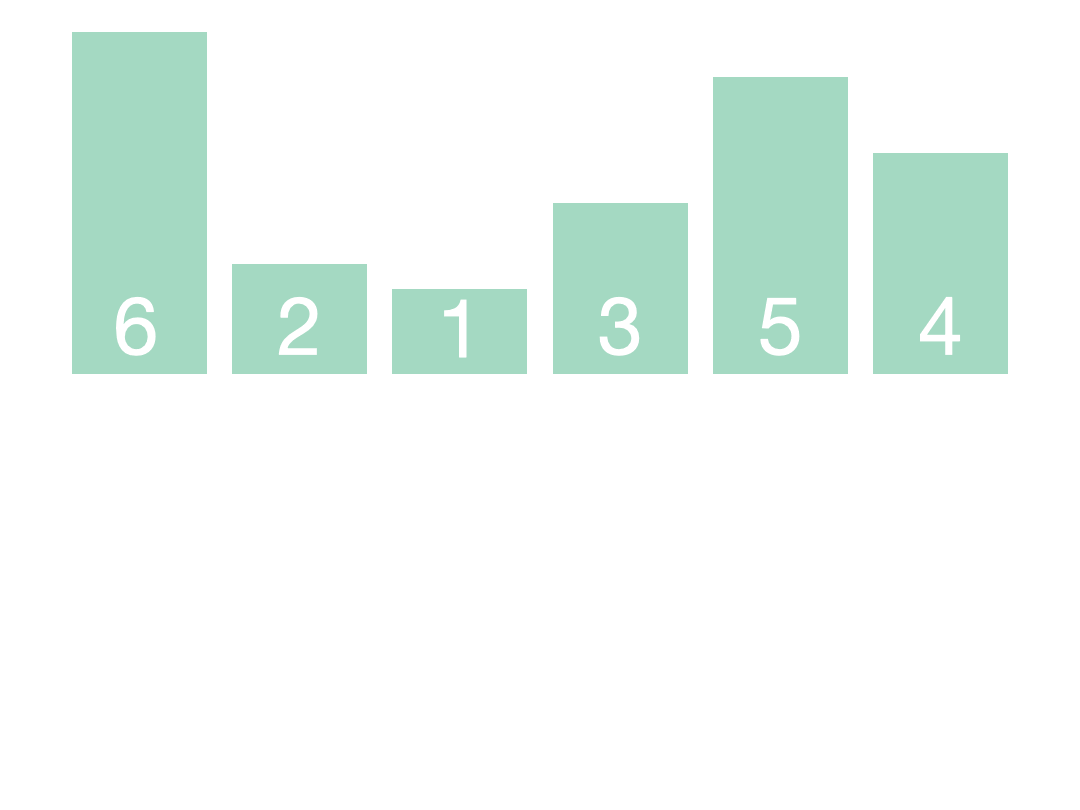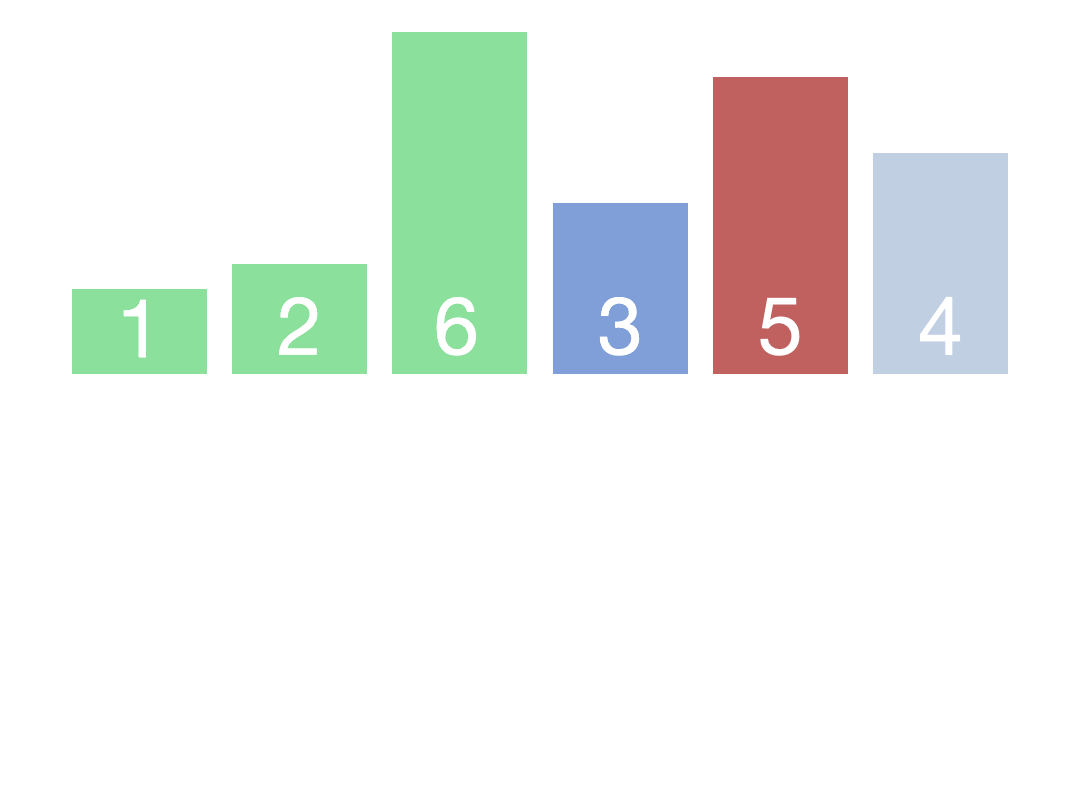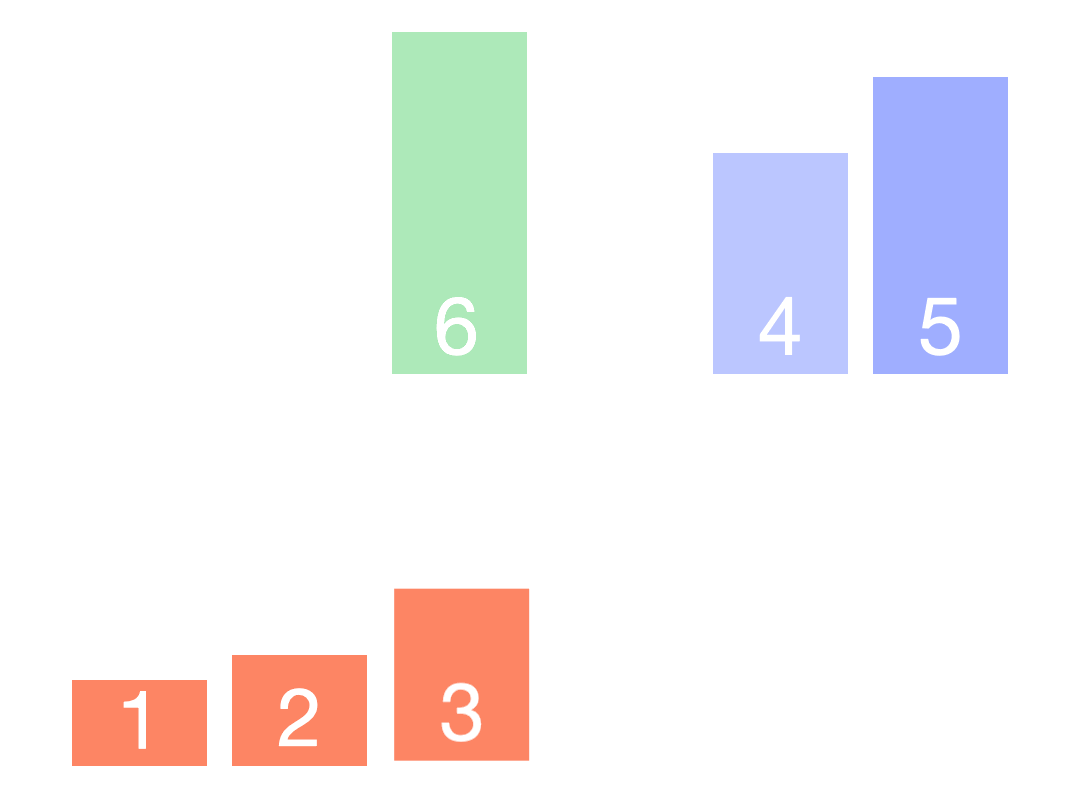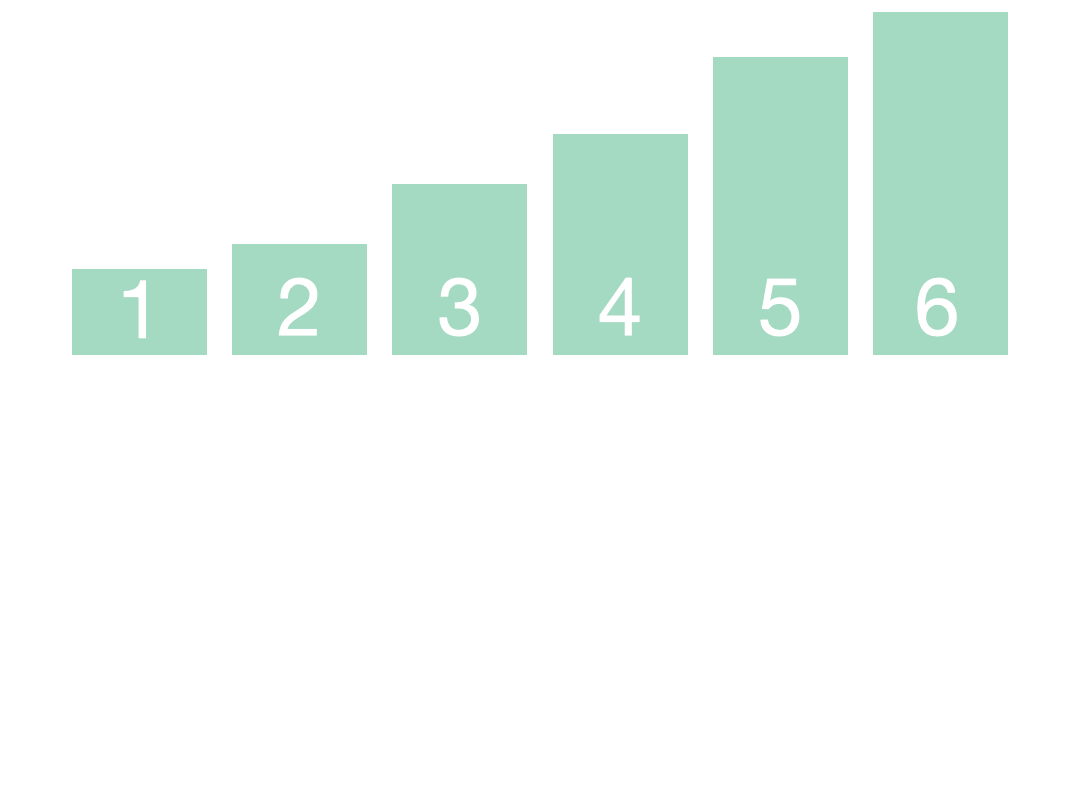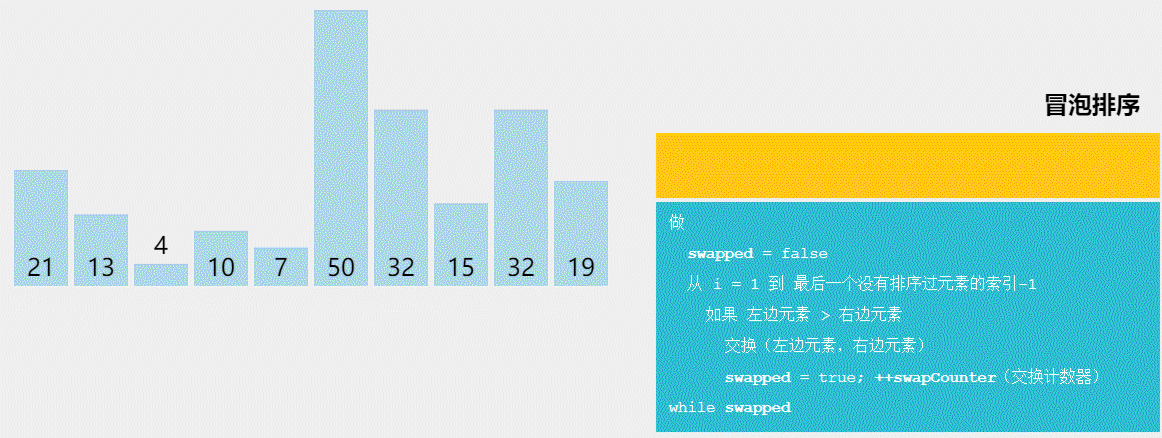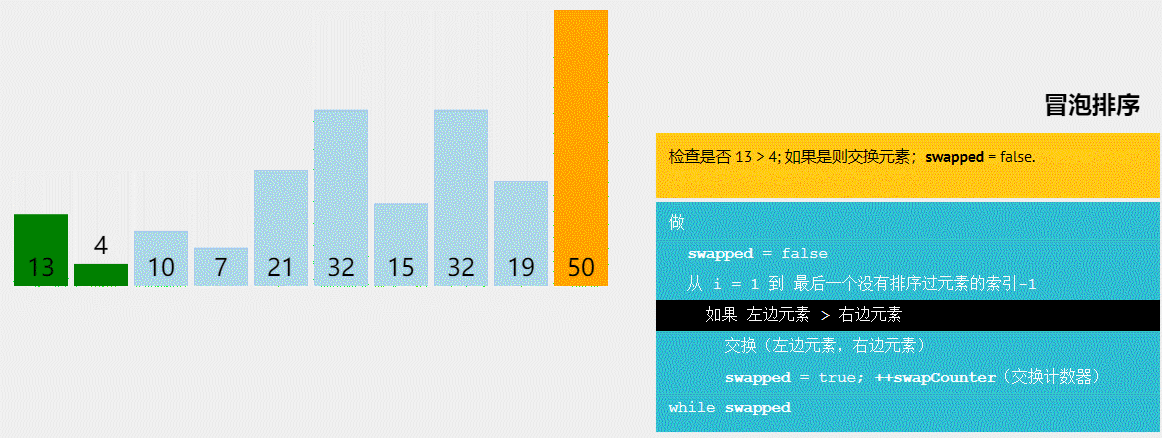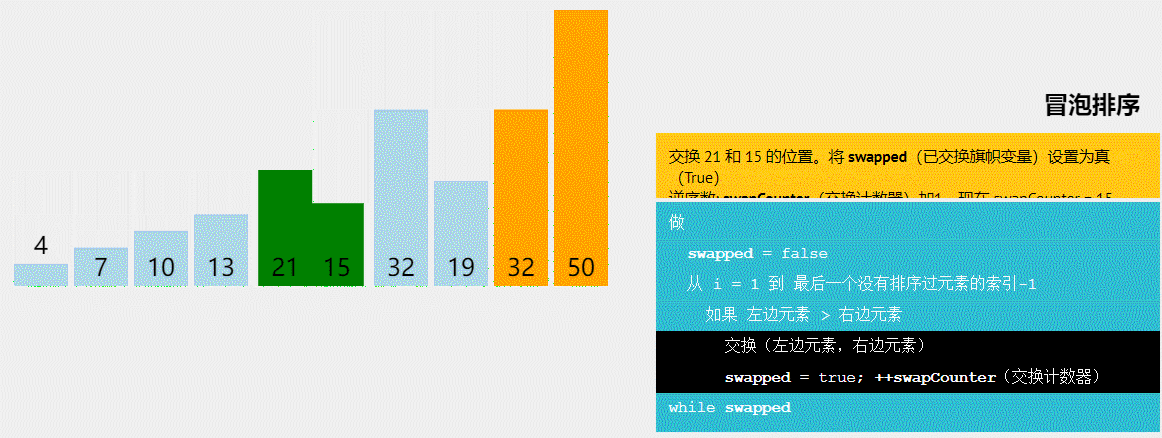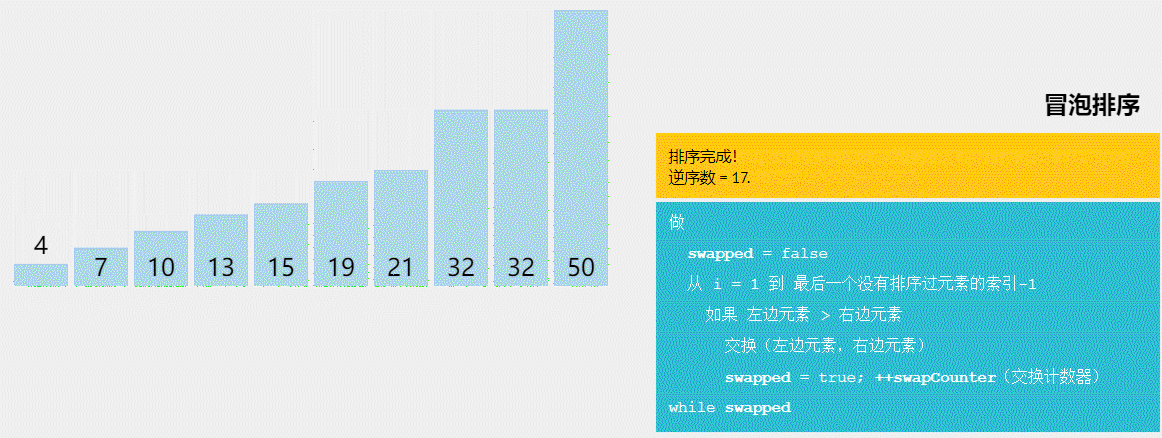408复试day2(7大排序算法)-Toy模板网

这篇具有很好参考价值的文章主要介绍了408复试day2(7大排序算法)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数据结构

7大排序算法总结：
首先排序分为内排序和外排序：
内排序是指待排序的记录放置在内存，而外排序是指排序的过程中需要对内存进行访问。其中稳定的排序有“插冒归”，即插入排序、冒泡排序、归并排序。
1.冒泡排序
算法原理：
①初始时有序区为空，即全部记录为无序区；
②在无序区中从后往前依次比较相邻记录，如果是逆序，则交换
③每趟排序时，无序区关键字最小的记录被逐渐交换到有序区的第一位，即加入到有序区
④如果一趟排序时没有发生过交换，则提前结束
代码实现：

void BubbleSort(ElemType L[],int n){
	int i,j;
	bool exchange;//记录是否发生交换的标志
	ElemType tem;
	for(i=0;i<n-1;i++){//最多进行n-1趟冒泡排序
		exchange=false;
		for(j=n-1;j>i;j--){//一趟冒泡排序
			if(L[j]<L[j-1]){//前大后小，即逆序就交换
				tem=L[j];
				L[j]=L[j-1];
				L[j-1]=tem;
				//交换过之后就改变exchange的值
				exchange=true;
			}
			if(exchange==false){
				return;
			}
		}
	}
}

冒泡排序的算法评价：
1>待排序序列为正序：比较次数n-1，交换次数为0；
2>待排序序列为逆序：比较次数为 n(n-1)/2,交换次数为 n(n-1)/2
2.快速排序
每趟排序使一个元素放入其最终位置，这一个元素称为枢轴，通常选排序的第一个元素。
枢轴把整个序列划分为两个子序列，利用递归分别对子序列重复上述相同过程，直至子序列长度为0或1为止。
划分方法：
选待排序列的第一个元素作为枢轴x
设置变量：
low指向序列的前端
high指向序列的后端
high和low依次从序列的两端交替向序列中央扫描，将小于x的元素移到枢轴的左边，将大于或等于x的元素移到枢轴的右边
代码实现

void QuickSort(ElemType L[],int s,int e){
	int low=s,high=e;//本次划分范围
	ElemType x = L[s];//序列第一个元素作为枢轴
	whlie(low<high){//内循环①从右到左查找比枢轴小的元素
		while(low<high&&L[high]>=x){
			high--;
		}
		L[low]=L[high];//将小数放在左侧小数序列中，内循环②从左到右查找比枢轴大或相等的元素
		while(low<high&&L[low]<x){
			low++;
		}
		L[high]=L[low];//将大数放在右侧大数序列中
	}//循坏结束时low、high重合
	L[low]=x;//确定枢轴的最终存放位置
	if(s<low-1) QuickSort(L,s,low-1);//对左侧小数序列进行递归划分
	if(high+1<e) QuickSort();//对右侧大数序列进行递归划分
}

算法性能分析：
时间复杂度：最好情况，每次都选到的是中间值作为枢轴O(nlog $_2$ n)；最坏情况，每次总是选到最小或最大元素作枢轴O(n²)
空间复杂度：需要栈空间实现递归
3.归并排序
归并排序将两个或多个有序序列合并为一个新的有序序列的过程，最简单的归并排序就是将两个有序序列合并为一个有序序列的过程，称为二路归并排序。
注意：只含有一个记录的序列显然是有序序列，将一个长度为n的无序序列看成是由n个长度为1的有序子序列组成。
把有些子序列中相邻的子序列两两归并，得到n/2个长度为2的有序子序列。
再把这些子序列两两归并，如此重复，直至形成一个长度为n的有序序列。
算法性能分析：
时间复杂度：O(nlog $_2$ n)，每一趟归并的时间复杂度为O(n)，总共需要进行log $_2$ n趟
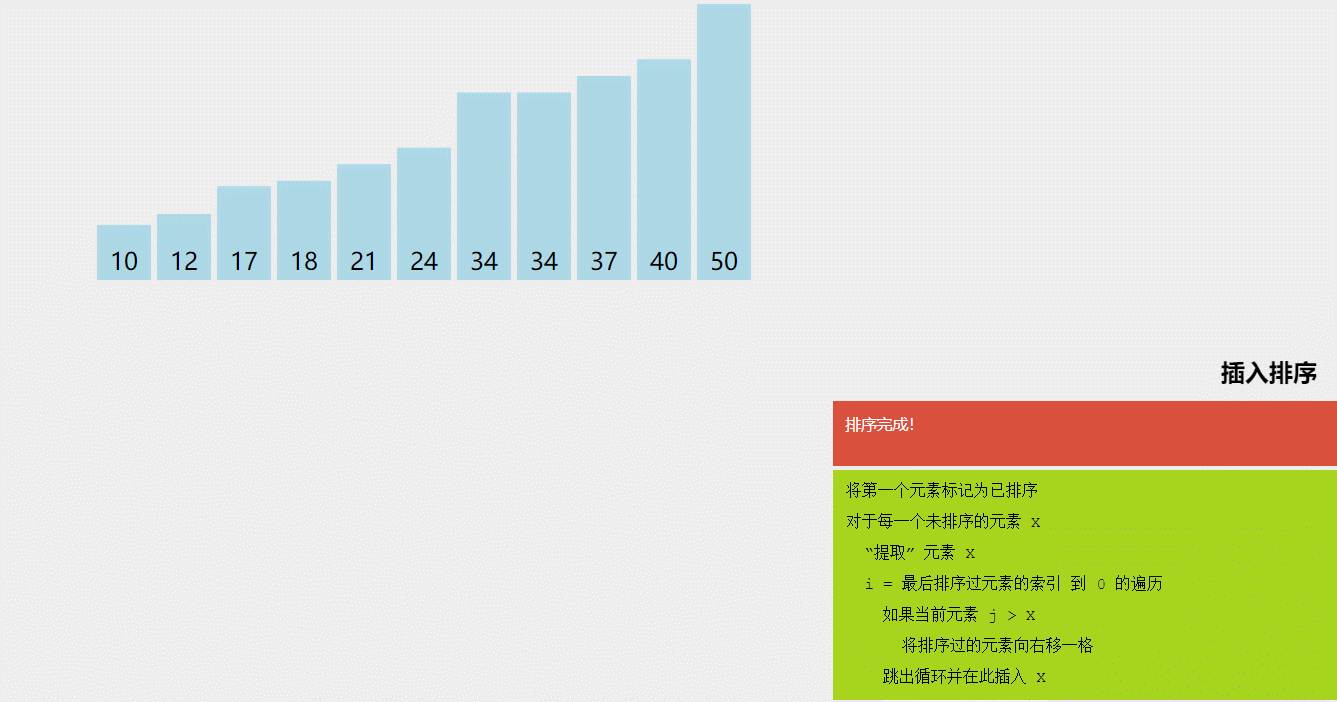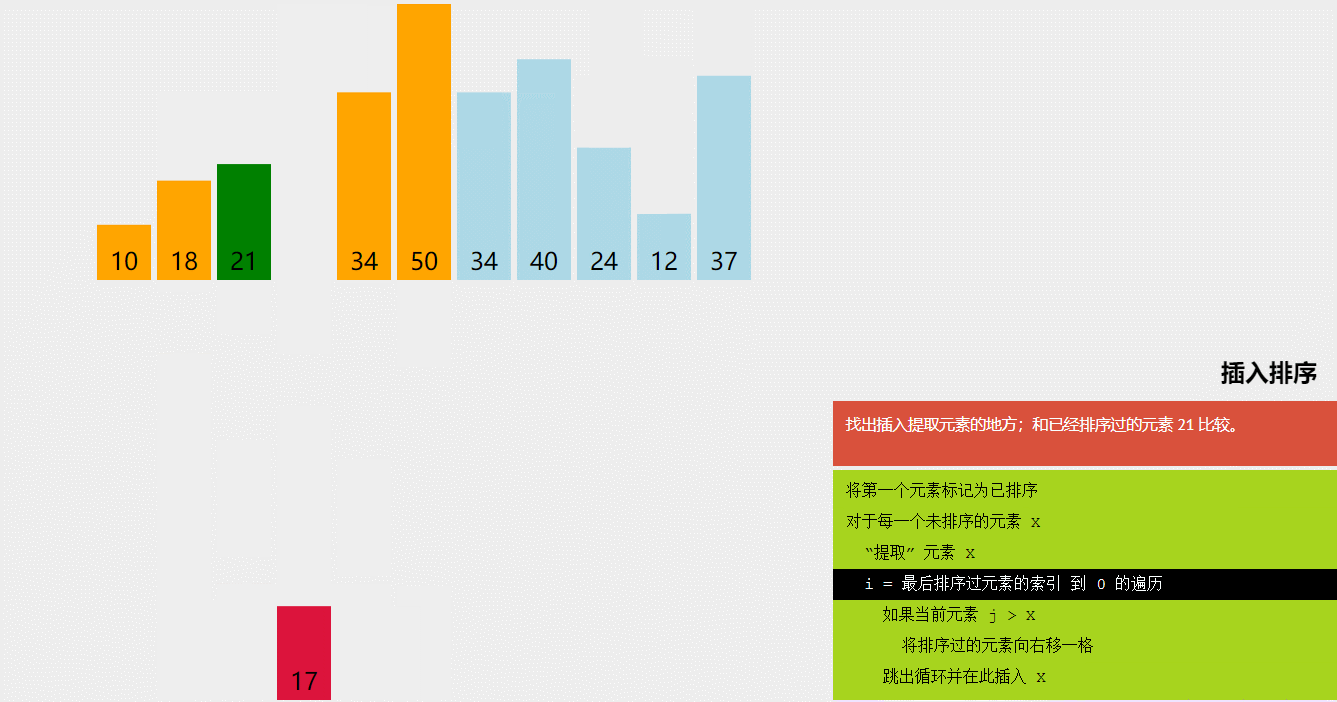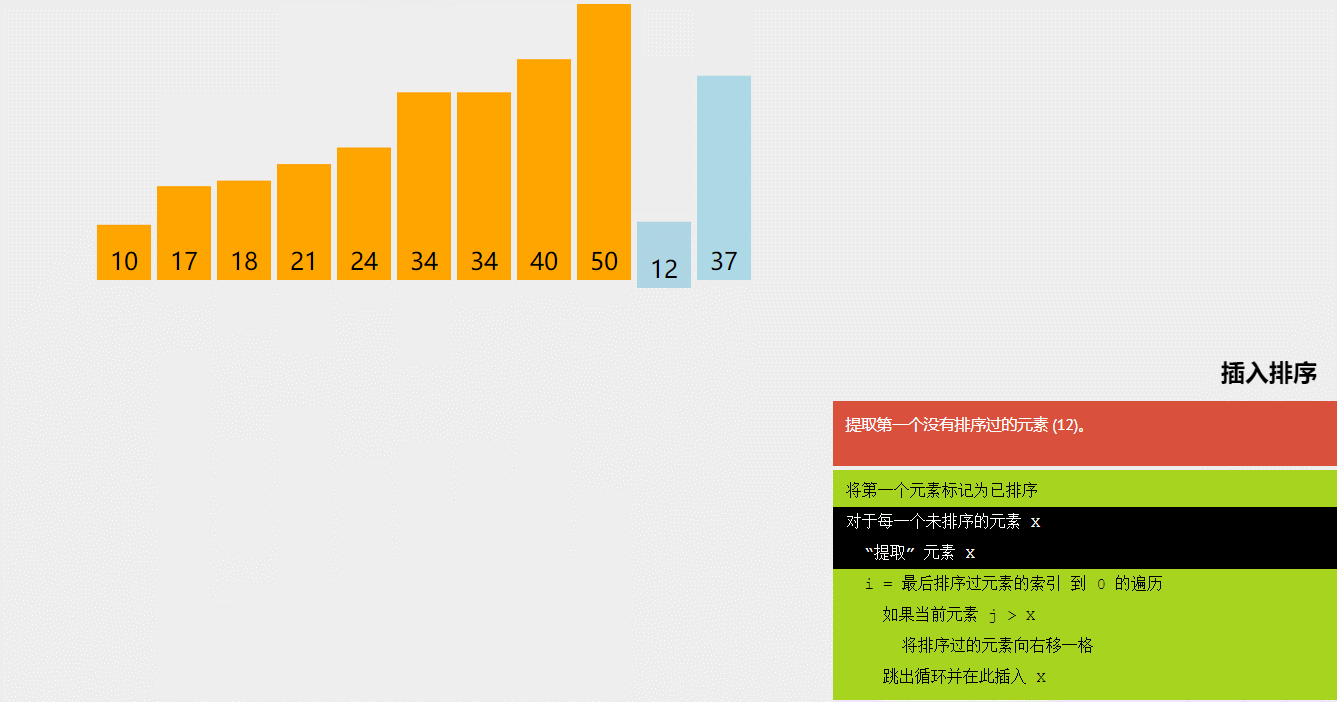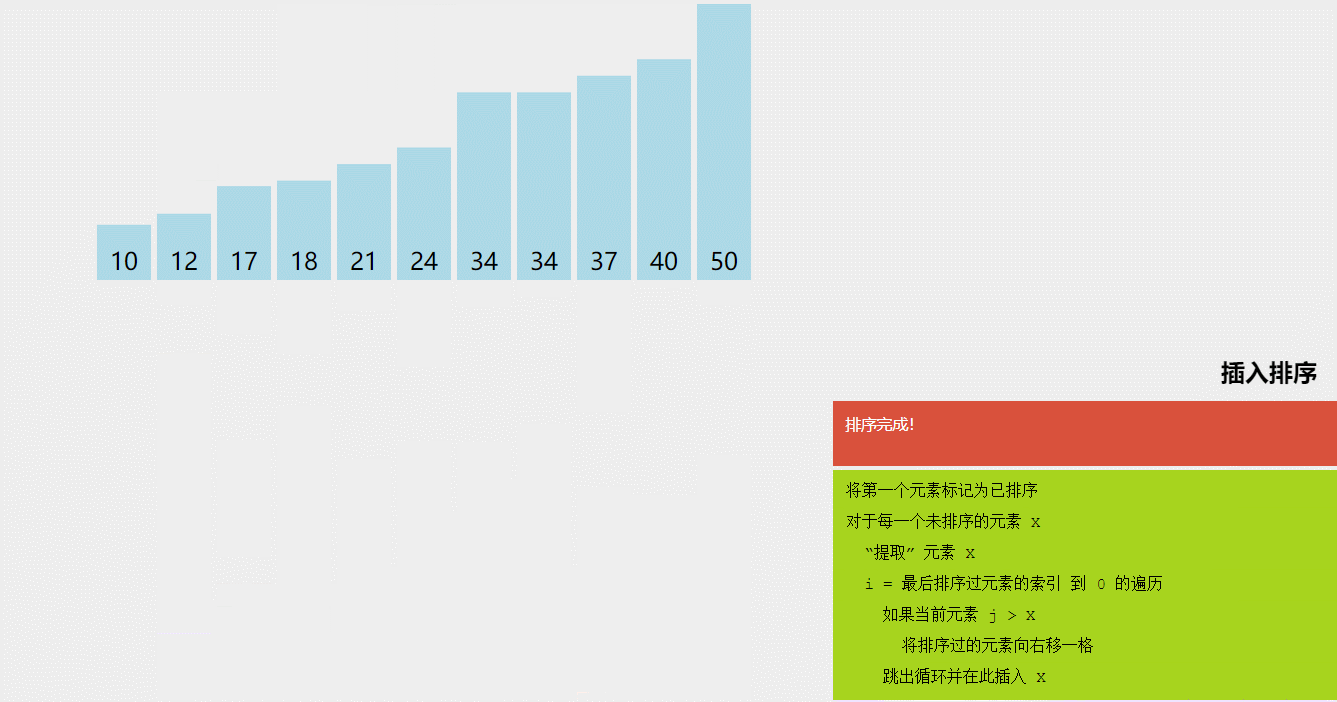
4.直接插入排序
序列分为有序区和无序区。每次取无序区的第一个元素按其关键字大小插入到有序区的适当位置。
初始时，指定待排序的第一个元素构成有序区。其余元素构成无序区。
每趟排序时，待插入元素为无序区的第一个元素。
从后向前比较，当前元素如大于待插入元素，则向后移动。
每次插入后，有序区增加一个元素，无序区减少一个元素
无序区为空时，排序结束。
性能分析：
基本操作：比较和移动的次数，决定了排序的时间性能。
待排序列为“正序”时，比较和移动的次数最少；
待排序列为“逆序”时，比较和移动的次数最多。
5.简单选择排序
序列分为有序区和无序区。每次从无序区选出关键字最小的元素与无序区的第一个元素交换，此时有序区多一个元素。
要点：
初始时，有序区为空，全部元素位于无序区
每趟排序时，选择无序区关键字最小的元素与无序区的第一个元素交换
每次选择并交换后，有序区增加一个元素，无序区减少一个元素
当无序区剩下最后一个元素时，排序即可结束。
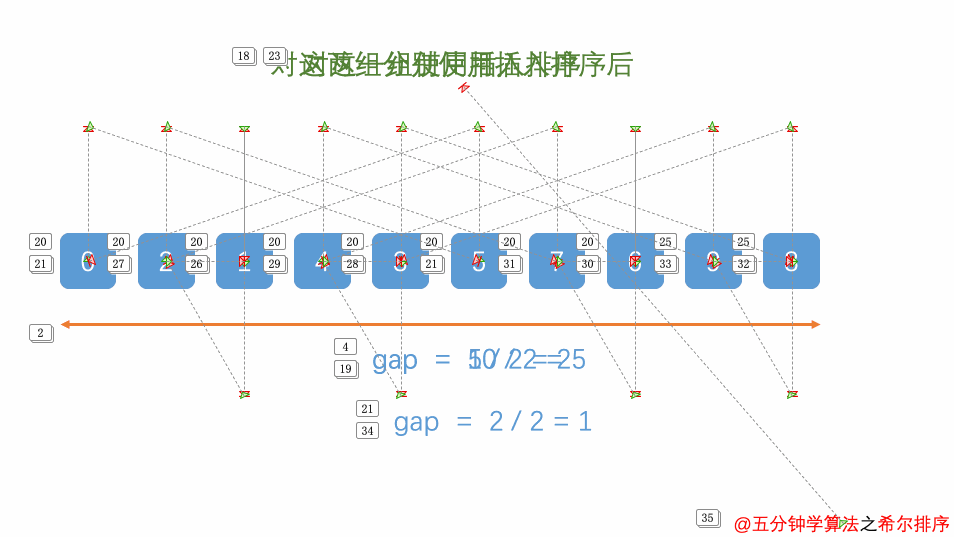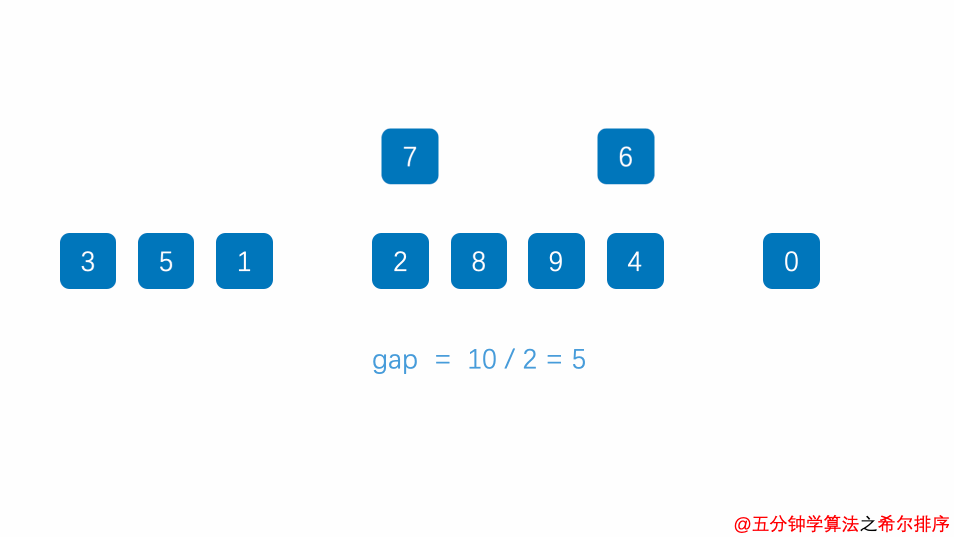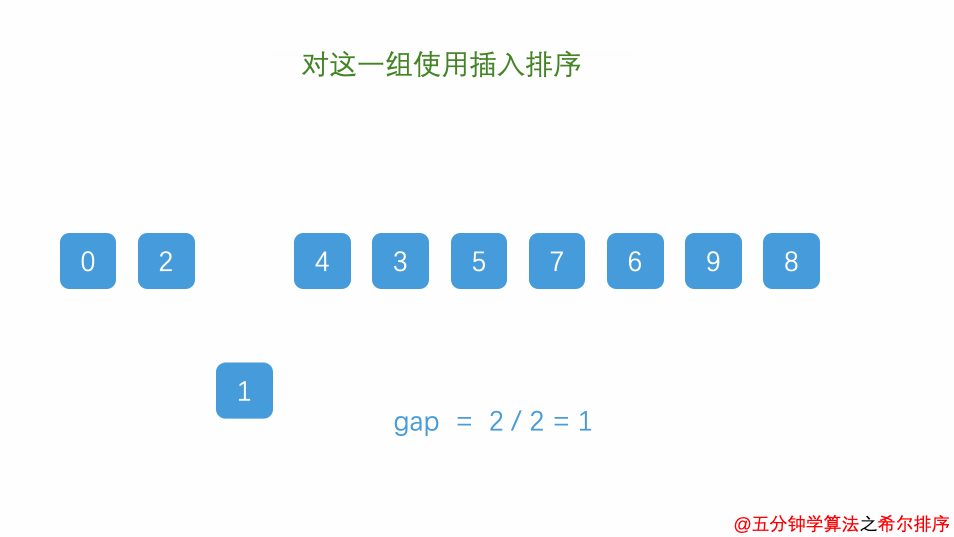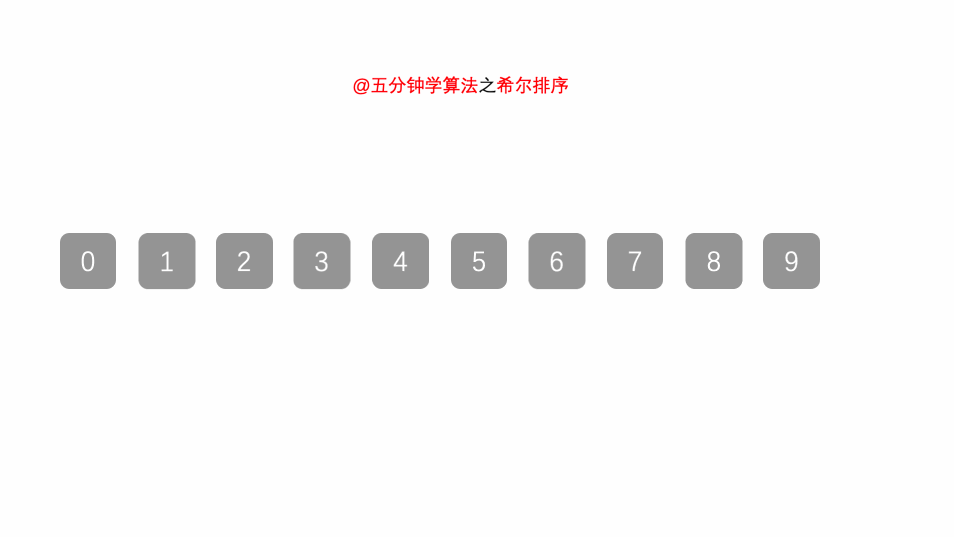
6.希尔排序
本质上是在插入排序算法的基础上进行的改进，就是先将待排序列分割成若干子序列分别进行插入排序，待整个序列中的记录“基本有序“时，再对全体记录进行一次直接插入排序
首先选择一个增量序列t1,t2……tk.令tk=1
按增量序列个数k，对序列进行k趟排序
每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m的子序列，分别对各子表进行直接插入排序。仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。
7.堆排序
即要满足堆积的性质，即子结点的键值一定大于或小于其父结点（根节点），其中每个结点的值大于等于其左右孩子结点的值，称为大根堆（大顶堆），反之，若每个结点的值都小于等于其左右孩子结点的值，称为小根堆（小顶堆）。
原理：
1.将初始待排关键字序列（R1，R2…………Rn）构建成大顶堆，此堆为初始的无序区；
2.将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区（R1，R2…………Rn-1）和新的有序区（Rn）,且满足R[1,2，……n-1]<=R[n].
3.由于交换后新的堆顶R[1]可能会违反堆的性质，因此需要对当前无序区调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区和新的有序区。不断重复此过程直到有序区的元素个数为n-1，则排序完。文章来源地址https://www.toymoban.com/news/detail-617032.html