Linear Algebra 4 Every One
版权说明,以下我分享的都是一个名叫Kenji Hiranabe的日本学者,在github上分享的,关于Gilbert Strang教授所撰写的《Linear Algebra for Everyone》一书的总结,更像是一个非常精美的线性代数手册,欢迎大家下载收藏。如果我的的这篇分享文章中涉嫌侵犯版权,我会立即删除该文章。
具体文章的发布地址:
https://github.com/kenjihiranabe/The-Art-of-Linear-Algebra/blob/main/README-zh-CN.mdhttps://github.com/kenjihiranabe/The-Art-of-Linear-Algebra/blob/main/README-zh-CN.md
文章有英文版,日文版和中文版。
这是MIT Gilbert Strang老爷爷的个人官网:
Gilbert Strang's HomepageProf. Gilbert Strang's Home Page, MIT Math Dept. Containsrecent wavelet and applied math papers, textbooks, and shortcourseinformation.https://math.mit.edu/~gs/
这是他写的《Linear Algebra for Everyone》一书的下载地址:
Linear Algebra for Everyone, Gilbert Stranghttps://math.mit.edu/~gs/everyone/

以下全部都是手册中的截图:
文章作者与序言部分

理解矩阵的四种视角

向量与向量的乘法

注意:图中关于v1,v2的说明,后面会用到,v是向量的英文Vector的首字母。
v1表示行向量乘以列向量
v2表示列向量乘以行向量
矩阵与向量的乘法

Mv1,Mv2都表示矩阵乘以列向量,Mv2是重点。
M和v分别是矩阵的英文Matrix和向量的英文Vector的首字母。

vM1,vM2都表示一个行向量乘以矩阵,vM2是重点。
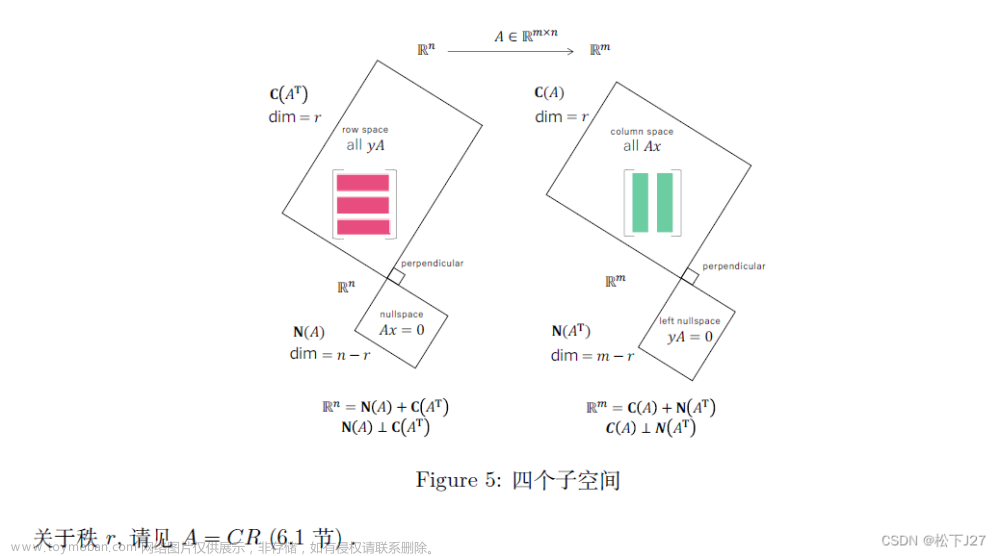
从四个角度理解矩阵与矩阵的乘法

MM1,MM2,MM3,MM4都表示矩阵与矩阵的乘法,个人认为MM2和MM3是重点。
矩阵与矩阵的乘法的另一种诠释
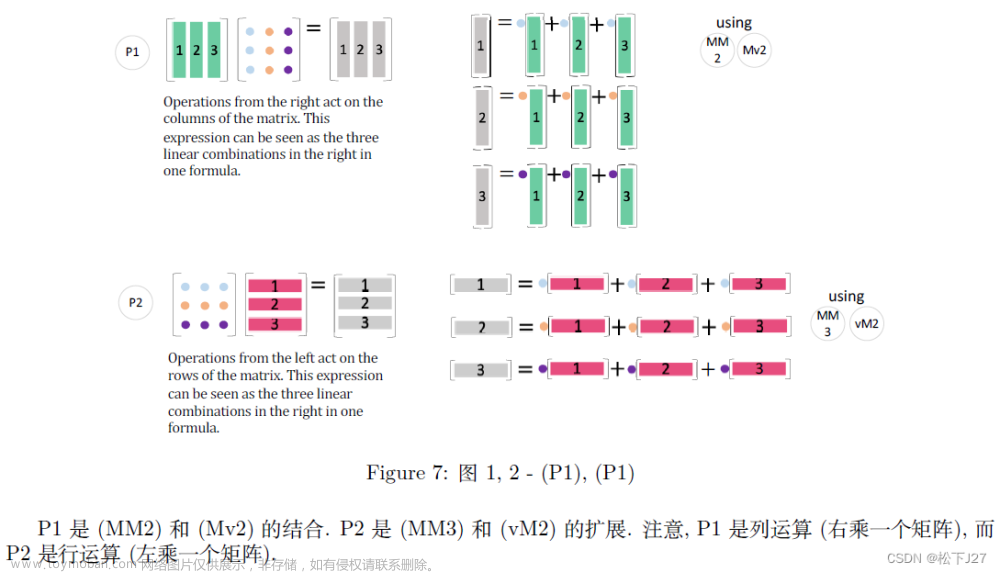
虽然,作者说P1是MM2和Mv2的组合,但我并不这么看,我觉得上图中,P1就是MM2,p2就是MM3。只是换了一种图示去说明。
矩阵与对角阵的乘法
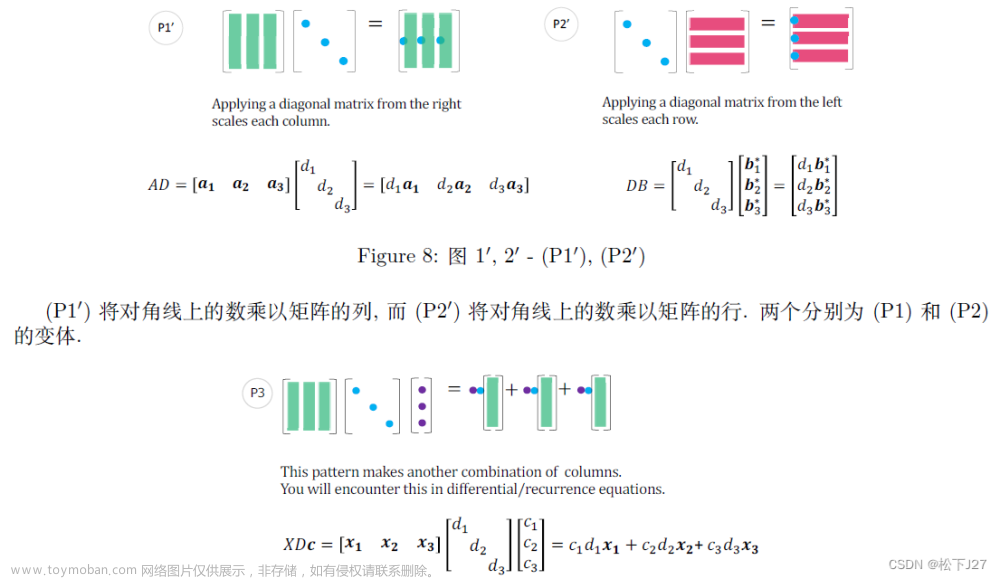
矩阵的五种分解方式
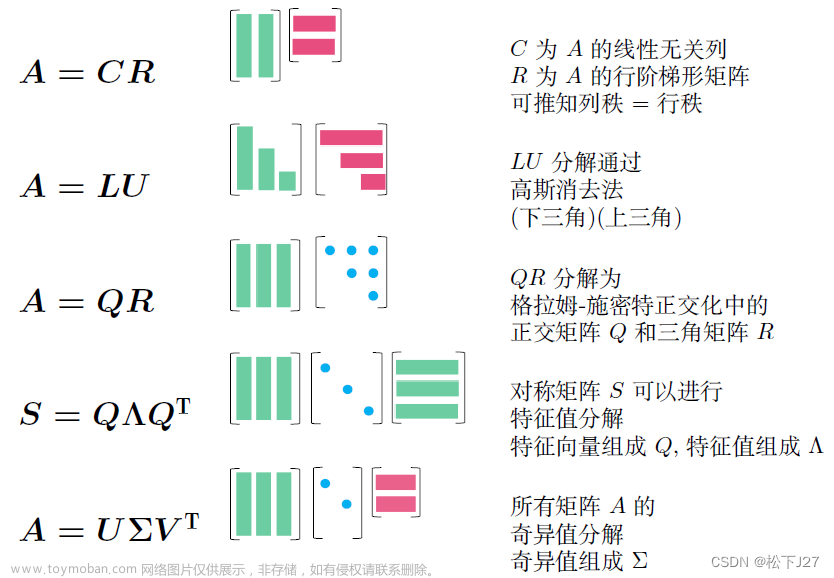
A=CR
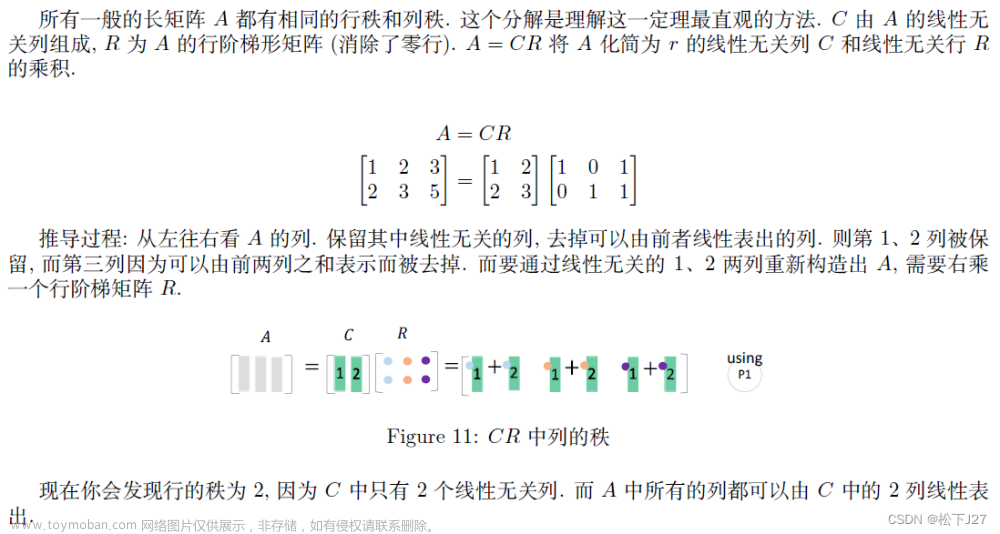
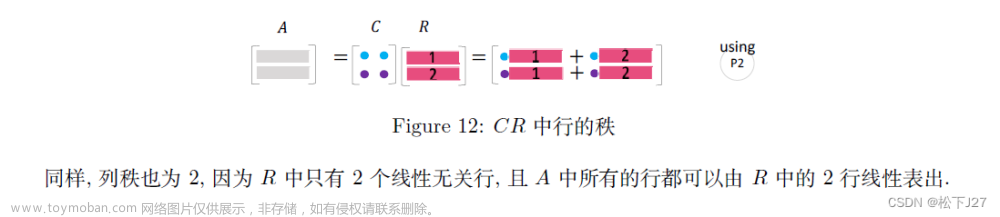
A=LU

A=QR

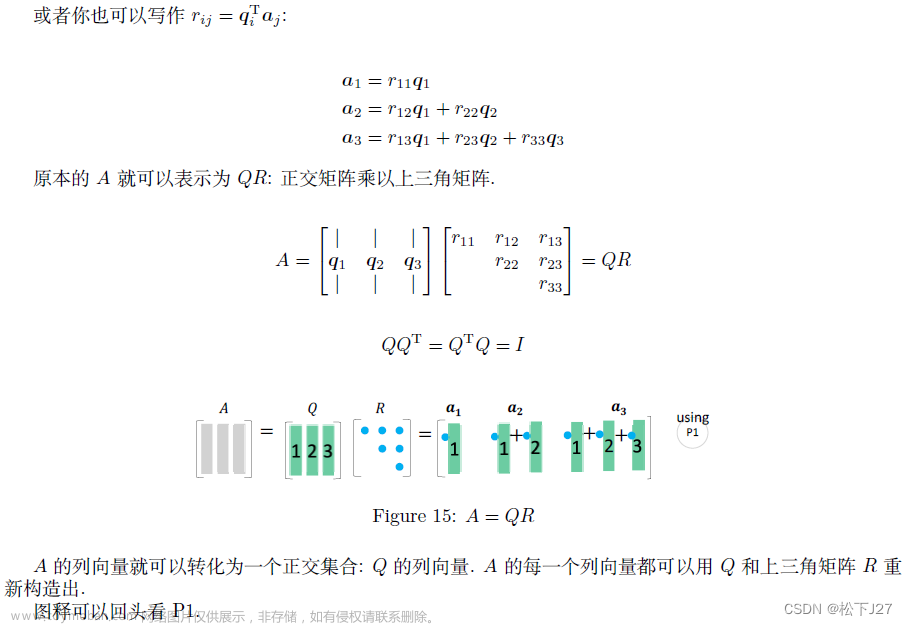

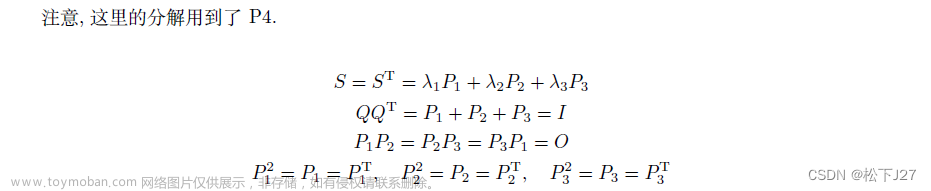

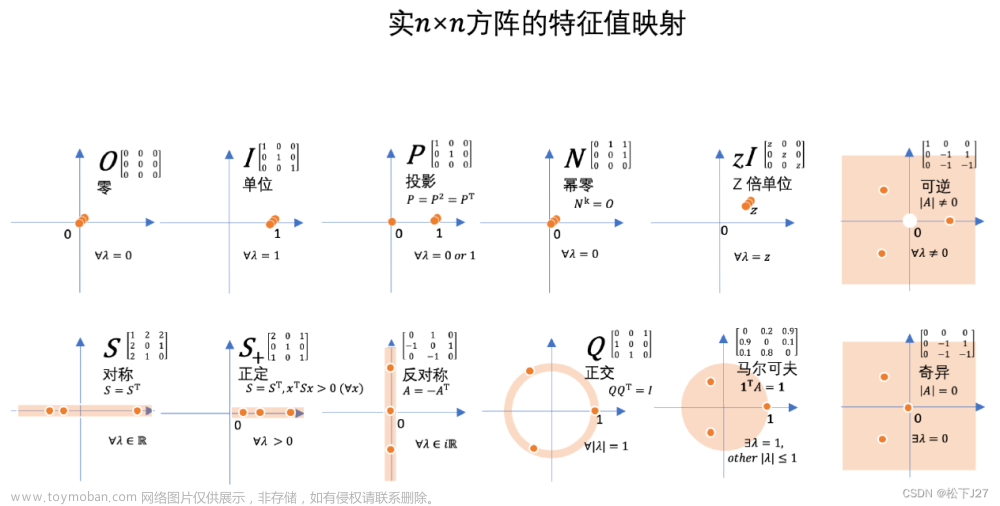
特征值全图
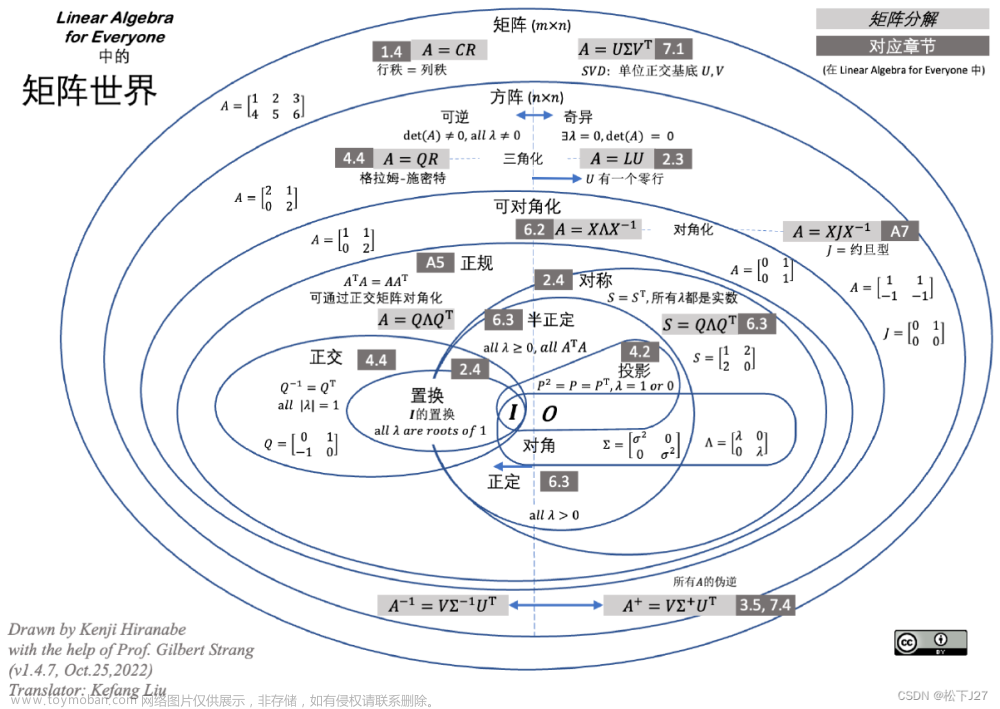
矩阵世界
(全文完)
作者 --- 松下J27
参考文献(鸣谢):
1,https://github.com/kf-liu/The-Art-of-Linear-Algebra-zh-CN/blob/main/The-Art-of-Linear-Algebra-zh-CN.pdf
2,https://github.com/kenjihiranabe/The-Art-of-Linear-Algebra/blob/main/README-zh-CN.md

(放一张strang老爷爷的视频截图)文章来源:https://www.toymoban.com/news/detail-617305.html
版权声明:文中的部分图片,文字或者其他素材,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 ----松下J27 文章来源地址https://www.toymoban.com/news/detail-617305.html
到了这里,关于线性代数 4 every one(线性代数学习资源分享)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!






