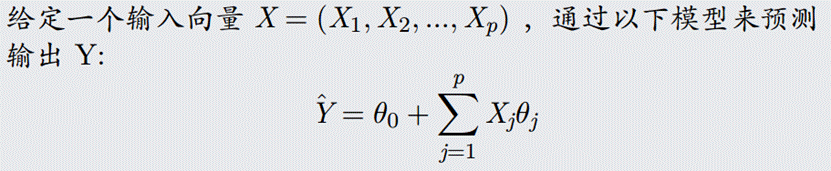Liner Regression with Multiple Variable
用向量实现的代码，单变量和多变量可以共用
多变量线性回归相当于是单变量的扩展，主要还是按照模型假设、构造代价函数和研究代价函数的最小值这样的思路展开。
与单变量线性回归不同的是，多变量线性回归还可能涉及到特征缩放的问题，主要原因是存在着不同尺度的特征变量，为了使得梯度下降能够快速地收敛，需要将这些特征变量统一尺度（类似于归一化的思想）
相比于单变量线性回归，多变量线性回归在求解代价函数的特征方程时，除了可以使用梯度下降法，还可以使用正则方程。根据特征变量的多少，灵活地选择这两种方法。
线性回归模型
数学表达式
\[f_{\vec{w}, b}(\vec{x}) = w_1x_1+…+w_nx_n+b
\]
or
\[ f_{\mathbf{w},b}(\mathbf{x}) = \mathbf{w} \cdot \mathbf{x} + b
\]
\[\mathbf{X} =
\begin{pmatrix}
x^{(0)}_0 & x^{(0)}_1 & \cdots & x^{(0)}_{n-1} \\
x^{(1)}_0 & x^{(1)}_1 & \cdots & x^{(1)}_{n-1} \\
\cdots \\
x^{(m-1)}_0 & x^{(m-1)}_1 & \cdots & x^{(m-1)}_{n-1}
\end{pmatrix}
\]
\[\mathbf{w} = \begin{pmatrix}
w_0 \\
w_1 \\
\cdots \\
w_{n-1}
\end{pmatrix}
\]
Feature scaling
当参数的差距在几个数量级时或参数导致模型溢出时，需要缩放特征，以提高梯度下降的速度文章来源：https://www.toymoban.com/news/detail-617494.html
数学表达式
| Feature scaling | Mean normalization | Z-score normalization |
|---|---|---|
| \(x_{j, scaled} = \frac{x_j} {max},x_j \in [0,1]\) | \(x_{j} = \frac{x_j - \mu_j}{max - min},x_j \in [-1, 1]\) | \(x_j = \frac{x_j - \mu_j}{\sigma_j},x_j \in [-3,3]\) |
代码
def zscore_normalize_features(X):
"""
computes X, zcore normalized by column
Args:
X (ndarray): Shape (m,n) input data, m examples, n features
Returns:
X_norm (ndarray): Shape (m,n) input normalized by column
mu (ndarray): Shape (n,) mean of each feature
sigma (ndarray): Shape (n,) standard deviation of each feature
"""
# find the mean of each column/feature
mu = np.mean(X, axis=0) # mu will have shape (n,)
# find the standard deviation of each column/feature
sigma = np.std(X, axis=0) # sigma will have shape (n,)
# element-wise, subtract mu for that column from each example, divide by std for that column
X_norm = (X - mu) / sigma
return (X_norm, mu, sigma)
Cost Function
数学表达式
\[J(w_1,…,w_n,b)
\]
Gradient Descent
数学表达式
\[\begin{align*} \text{repeat}&\text{ until convergence:} \; \lbrace \newline\;
& w_j = w_j - \alpha \frac{\partial J(\mathbf{w},b)}{\partial w_j} & \text{for j = 0..n-1}\newline
&b\ \ = b - \alpha \frac{\partial J(\mathbf{w},b)}{\partial b} \newline \rbrace
\end{align*}
\]
Normal equation
仅适用于线性回归 && 求解时不迭代文章来源地址https://www.toymoban.com/news/detail-617494.html
到了这里，关于【机器学习】多变量线性回归的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
