【分布式能源的选址与定容】基于多目标粒子群算法分布式电源选址定容规划研究（Matlab代码实现）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【分布式能源的选址与定容】基于多目标粒子群算法分布式电源选址定容规划研究（Matlab代码实现）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

目录

💥1 概述

1.1 功率损耗

编辑1.2 电压质量

1.3 DG总容量

📚2 运行结果

🌈3 Matlab代码实现

🎉4 参考文献

💥1 概述

参考文献：

【分布式能源的选址与定容】基于多目标粒子群算法分布式电源选址定容规划研究（Matlab代码实现）,分布式,能源,算法

本文采用的是换一个算法解决，基于基于多目标粒子群算法分布式电源选址定容规划研究。

将可再生能源的分布式发电技术与大电网结合，是普遍公认的节能减排、绿色环保、安全可靠的电力系统运行方式，是电力发展的方向。分布式电源(DG)是指在一定的地域范围内，以分散方式布置在用户附近，与环境兼容的小型模块化发电单元，其发电功率为几千瓦到几十兆瓦。

分布式发电系统目前大多与配电网并网运行。ＤＧ入电网后，会对配电网的潮流分布产生影响，进而可以优化配电网络，缓解配电网输配用电压力。但是由于ＤＧ的投入和退出有很大的随机性，且输出功率的稳定性易受环境影响，因此，ＤＧ的不当接入会对电网产生诸多负面影响，如影响配电网的稳定性及电压质量，产生谐波等。这些影响的大小与ＤＧ的容量和接入位置有很大关，因此，ＤＧ的选址定容是在ＤＧ规划阶段中需要考虑的重点问题。

由于规划的优化目标较为单一，传统的规划方法无法很好地解决这一问题。近年来，考虑电压、电流质量和环境等因素的多目标优化迅速发展，但量纲的不统一，使得求解的复杂性大大提高，给多目标优化提出了新的挑战。本文在研究标准粒子群优化算法的基础上，针对配电网中ＤＧ的选址定容问题，建立了包括有功率损耗、电压质量及接入ＤＧ的总容量为目标函数的数学模型，基于多目标粒子群算法分布式电源选址定容规划研究，用Matlab解决之。

1.1 功率损耗

电能在从发电端传输到负载端的过程中,输电线路上产生的电能损耗不可址见，只议r地减小有功功率损耗,提理地配置配电网中的 DG,可以有效地减小有功功率损耗，提高发电利用率,节约能量。基于有功功率损耗的目标函数最优数学表达式为:

1.2 电压质量

某些状况下,电力系统在遭受干扰后的几秒或几分钟内，系统中的某些母线电压可能经历大幅度﹑持续性降低,从而使得系统的完整性遭到破坏,功率不能正常地传送给用户。这种灾变称为系统电压不稳定﹐其灾难后果则是电压崩溃。通常用静态电压稳定指标来表示系统电压稳定性。配电网中电
压质量受配电系统的电压稳定性影呵。今乂术用能T网P电压基于期望电压的方差来描述电压质量。基于电压质量的目标函数最优数学表达式为:

【分布式能源的选址与定容】基于多目标粒子群算法分布式电源选址定容规划研究（Matlab代码实现）,分布式,能源,算法

1.3 DG总容量

在实际应用中不仅要考虑改善电网带来的经济效应,还需要考虑DG安装、运行和维护的成本费用问题。本文中不涉及经济模型,仅考虑接入配电网的DG总容量。基于DG总容量的目标函数最优数学表达式为:
【分布式能源的选址与定容】基于多目标粒子群算法分布式电源选址定容规划研究（Matlab代码实现）,分布式,能源,算法

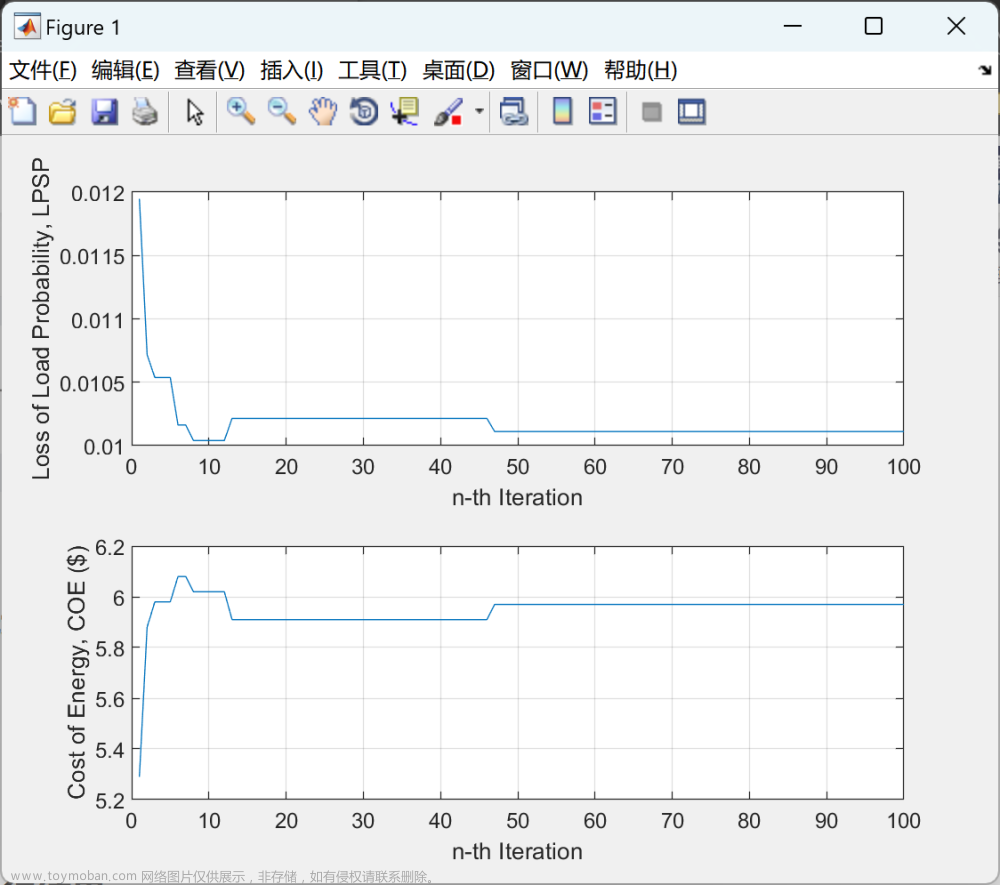
📚2 运行结果

【分布式能源的选址与定容】基于多目标粒子群算法分布式电源选址定容规划研究（Matlab代码实现）,分布式,能源,算法

🌈3 Matlab代码实现

部分代码：

%% 雅可比矩阵
J=[jpt jpv; jqt jqv];
X = (inv(J))*M;%偏差
%% 相位偏差
dTh = X(1:nbus-1);
%% 电压偏差
dV = X(nbus:end);
[e1,d1,n1]=eig(JR);%计算矩阵A的特征值和特征向量的函数是eig(A)[V,D,W] = eig(A)，[V,D,W] = eig(A)返回满矩阵 W，其列是对应的左特征向量，使得 W’A = DW’。
%diag(A),若A是一个矩阵，则diag函数的作用是产生提取矩阵的对角线；若a是一个向量，则diag函数的作用是产生一个对角线为a的矩阵
%% 目标2 电压稳定性
f2val=max(1./diag((d1)))*max(abs(dQ));%目标2，稳定性
del(2:nbus) = dTh + del(2:nbus);
k = 1;
for i = 2:nbus
if type(i) == 3
V(i) = dV(k) + V(i);
k = k+1;
end
end
%% 目标2和目标3
tval=sum(1./diag((d1)));
po_val=flow_cal(nbus,V,del,BMva);
f1val=sum(po_val);%各支路网损和
f3val=sum(datain(5:8));%DG容量和

fout=[f1val; f2val; f3val];

for i = 1 : N
% Number of individuals that dominate this individual
individual(i).n = 0;
% Individuals which this individual dominate
individual(i).p = [];
for j = 1 : N
dom_less = 0;
dom_equal = 0;
dom_more = 0;
for k = 1 : M
if (x(i,V + k) < x(j,V + k))
dom_less = dom_less + 1;
elseif (x(i,V + k) == x(j,V + k))
dom_equal = dom_equal + 1;
else
dom_more = dom_more + 1;
end
end
if dom_less == 0 && dom_equal ~= M %大于等于的情况
individual(i).n = individual(i).n + 1;
elseif dom_more == 0 && dom_equal ~= M %小于等于的情况
individual(i).p = [individual(i).p j];
end
end
if individual(i).n == 0
x(i,M + V + 1) = 1;
F(front).f = [F(front).f i];
end
end
% Find the subsequent fronts
while ~isempty(F(front).f)
Q = [];
for i = 1 : length(F(front).f)
if ~isempty(individual(F(front).f(i)).p)
for j = 1 : length(individual(F(front).f(i)).p)
individual(individual(F(front).f(i)).p(j)).n = ...
individual(individual(F(front).f(i)).p(j)).n - 1;
if individual(individual(F(front).f(i)).p(j)).n == 0
x(individual(F(front).f(i)).p(j),M + V + 1) = ...
front + 1;
Q = [Q individual(F(front).f(i)).p(j)];
end
end
end
end
front = front + 1;
F(front).f = Q;
end

[temp,index_of_fronts] = sort(x(:,M + V + 1));
for i = 1 : length(index_of_fronts)
sorted_based_on_front(i,:) = x(index_of_fronts(i),:);
end
current_index = 0;

%% Crowding distance
%The crowing distance is calculated as below
% ?For each front Fi, n is the number of individuals.
% ?initialize the distance to be zero for all the individuals i.e. Fi(dj ) = 0,
% where j corresponds to the jth individual in front Fi.
% ?for each objective function m
% * Sort the individuals in front Fi based on objective m i.e. I =
% sort(Fi,m).
% * Assign infinite distance to boundary values for each individual
% in Fi i.e. I(d1) = ? and I(dn) = ?
% * for k = 2 to (n ? 1)
% ?I(dk) = I(dk) + (I(k + 1).m ? I(k ? 1).m)/fmax(m) - fmin(m)
% ?I(k).m is the value of the mth objective function of the kth
% individual in I

% Find the crowding distance for each individual in each front
for front = 1 : (length(F) - 1)
% objective = [];
distance = 0;
y = [];
previous_index = current_index + 1;
for i = 1 : length(F(front).f)
y(i,:) = sorted_based_on_front(current_index + i,:);
end
current_index = current_index + i;
% Sort each individual based on the objective
sorted_based_on_objective = [];
for i = 1 : M
[sorted_based_on_objective, index_of_objectives] = ...
sort(y(:,V + i));
sorted_based_on_objective = [];
for j = 1 : length(index_of_objectives)
sorted_based_on_objective(j,:) = y(index_of_objectives(j),:);
end
f_max = ...
sorted_based_on_objective(length(index_of_objectives), V + i);
f_min = sorted_based_on_objective(1, V + i);
y(index_of_objectives(length(index_of_objectives)),M + V + 1 + i)...
= Inf;
y(index_of_objectives(1),M + V + 1 + i) = Inf;
for j = 2 : length(index_of_objectives) - 1
next_obj = sorted_based_on_objective(j + 1,V + i);
previous_obj = sorted_based_on_objective(j - 1,V + i);
if (f_max - f_min == 0)
y(index_of_objectives(j),M + V + 1 + i) = Inf;
else
y(index_of_objectives(j),M + V + 1 + i) = ...
(next_obj - previous_obj)/(f_max - f_min);
end
end
end
distance = [];
distance(:,1) = zeros(length(F(front).f),1);
for i = 1 : M
distance(:,1) = distance(:,1) + y(:,M + V + 1 + i);
end
y(:,M + V + 2) = distance;
y = y(:,1 : M + V + 2);
z(previous_index:current_index,:) = y;
end
f = z();