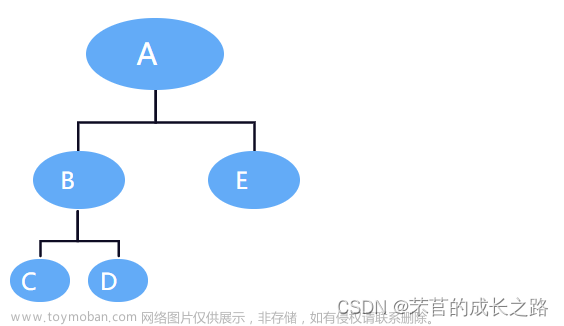
学习树之前,我们已经了解了二叉树的顺序存储和链式存储,哪么我们如何来存储普通型的树结构的数据?如下图1:

如图1所示,这是一颗普通的树,我们要如何来存储呢?通常,存储这种树结构的数据的方法有3中:
- 双亲表示法。
- 孩子表示法。
- 孩子兄弟表示法。
双亲表示法
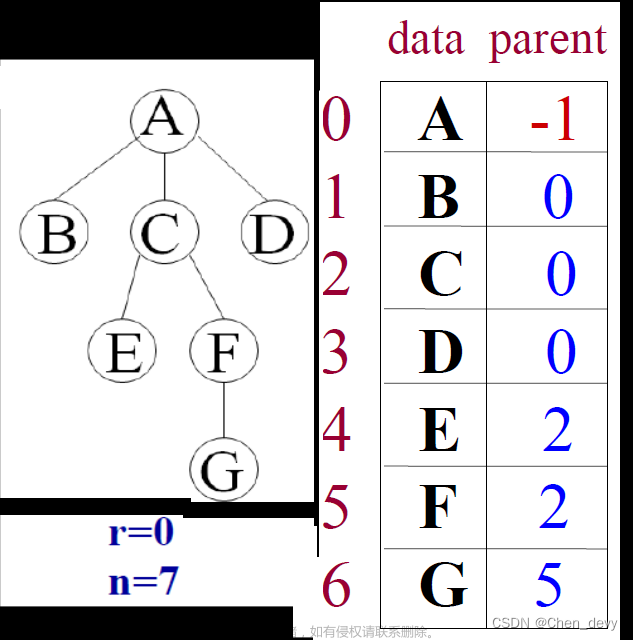
双亲表示法采用顺序表(也就是数组)存储普通树,核心思想:顺序存储各个节点的同时,给各个节点附加一个记录其父节点位置的变量。
注意:根结点没有父节点,因此根结点记录父节点位置的变量一般为-1。
例如,采用双亲表示法存储图1中的普通树,其存储状态如图2所示:

图2存储普通树转化为代码为:
#define MAX_SIZE 100//定义树中结点最大数量
typedef struct node{
char data;//树中结点的数据
int parent;//结点的父节点再数组中的位置下标
};
typedef struct {
node arr[MAX_SIZE];//存放树中所有结点
int n;//节点数
}Tree;
因此,存储图1中普通树的实现代码为:
#include "iostream"
using namespace std;
#define MAX_SIZE 100//定义树中结点最大数量
typedef struct node{
char data;//树中结点的数据
int parent;//结点的父节点再数组中的位置下标
};
typedef struct {
node arr[MAX_SIZE];//存放树中所有结点
int n;//节点数
}Tree;
Tree Init(Tree tree){
cout << "请输入结点个数:" << endl;
cin >> tree.n;
cout << "请输入结点的值其双亲位于数组中的位置下标:" << endl;
for(int i = 0; i < tree.n; i++){
cin >> tree.arr[i].data >> tree.arr[i].parent;
}
return tree;
}
void FindParent(Tree tree){
char a;
bool IsFind = false;
cout << "请输入要查询的节点值:" << endl;
cin >> a;
for(int i = 0; i < tree.n; i++){
if(tree.arr[i].data == a){
IsFind = true;
cout << a << "的父节点为" << tree.arr[tree.arr[i].parent].data << ",存储位置下标为" << tree.arr[i].parent << endl;
break;
}
}
}
int main(){
Tree tree;
for(int i = 0; i < MAX_SIZE; i++){
tree.arr[i].parent = -1;
tree.arr[i].data = ' ';
}
tree = Init(tree);
FindParent(tree);
return 0;
}
程序运行实例:
请输入结点个数:
10
请输入结点的值其双亲位于数组中的位置下标:
R -1
A 0
B 0
C 0
D 1
E 1
F 3
G 6
H 6
K 6
请输入要查询的节点值:
C
C的父节点为R,存储位置下标为0
孩子表示法
孩子表示法是采用“顺序表+链表”的组合结构,其存储过程是:从树的根结点开始,使用顺序表依次存储树中各个节点,需要注意的是,与双亲表示法不同,孩子表示法会给各个节点配备一个链表,用于存储各个节点的孩子节点位于顺序表中的位置。
如果孩子没有叶子节点,则该节点的链表为空链表。
例如,使用孩子表示法存储图3a中的树,则最终存储状况如图3b所示:

代码实现如下:
#include "iostream"
using namespace std;
#define MAX_SIZE 100//定义树中结点最大数量
typedef struct node{
int child;//链表中每个结点存储的是数据再数组中存储的位置下标
struct node *next;
};
typedef struct {
char data;//结点的数据
node * FirstChild;//孩子链表的头节点
}box;
typedef struct {
box arr[MAX_SIZE];//存放树中所有结点
int n, r;//节点数和树根的位置
}Tree;
Tree Init(Tree tree){
cout << "请输入结点个数:";
cin >> tree.n;
for(int i = 0; i < tree.n; i++){
cout << "输入第" << i + 1 << "个节点的值:" ;
cin >> tree.arr[i].data;
tree.arr[i].FirstChild = new node;
tree.arr[i].FirstChild->next = NULL;
cout << "输入结点" << tree.arr[i].data << "的孩子结点的数量:";
int num = 0;
cin >> num;
if(num != 0){
node *p = tree.arr[i].FirstChild;
for(int j = 0; j < num; j++){
node *ptr = new node;
ptr->next = NULL;
cout << "输入第" << j + 1 << "个孩子节点在顺序表中的位置: ";
cin >> ptr->child;
p->next = ptr;
p = p->next;
}
}
}
return tree;
}
void FindKids(Tree tree, char ch){
bool IsFind = false;
for(int i = 0; i < tree.n; i++){
if(tree.arr[i].data == ch){
node *p = tree.arr[i].FirstChild->next;
while(p){
IsFind = true;
cout << tree.arr[p->child].data;
p = p->next;
}
break;
}
}
}
int main(){
Tree tree;
tree.r = 0;//默认根结点的下标为0
for(int i = 0; i < MAX_SIZE; i++){
tree.arr[i].FirstChild = NULL;
}
tree = Init(tree);
FindKids(tree, 'F');//找出结点F的所有孩子结点
return 0;
}
程序运行结果如下:
请输入结点个数:10
输入第1个节点的值:R
输入结点R的孩子结点的数量:3
输入第1个孩子节点在顺序表中的位置: 1
输入第2个孩子节点在顺序表中的位置: 2
输入第3个孩子节点在顺序表中的位置: 3
输入第2个节点的值:A
输入结点A的孩子结点的数量:2
输入第1个孩子节点在顺序表中的位置: 4
输入第2个孩子节点在顺序表中的位置: 5
输入第3个节点的值:B
输入结点B的孩子结点的数量:0
输入第4个节点的值:C
输入结点C的孩子结点的数量:1
输入第1个孩子节点在顺序表中的位置: 6
输入第5个节点的值:D
输入结点D的孩子结点的数量:0
输入第6个节点的值:E
输入结点E的孩子结点的数量:0
输入第7个节点的值:F
输入结点F的孩子结点的数量:3
输入第1个孩子节点在顺序表中的位置: 7
输入第2个孩子节点在顺序表中的位置: 8
输入第3个孩子节点在顺序表中的位置: 9
输入第8个节点的值:G
输入结点G的孩子结点的数量:0
输入第9个节点的值:H
输入结点H的孩子结点的数量:0
输入第10个节点的值:K
输入结点K的孩子结点的数量:0
找出节点 F 的所有孩子节点:GHK
使用孩子表示法存储的树结构,正好和双亲表示法相反,适用于 查找某个节点的孩子结点,不适用于查找父节点。
其实,我们也可以将双亲表示法和孩子表示法相互结合,就可以得到如图4所示:

使用图4结果存储普通树,技能快速找到指定节点的父节点,也能快速找到指定结点的孩子结点。
孩子兄弟表示法
孩子兄弟表示法:采用的是链式存储结构,其思想是,从树的根结点开始,依次用链表存储各个节点的孩子结点和兄弟节点。
所以,该链表中的结点包括3个部分,如图5所示:
- 结点的值。
- 指向孩子结点的指针。
- 指向兄弟结点的指针。

代码表示如下:
typedef struct node{
char data;
struct node *ForstChild, *NextSibling;
};
还是以图1为例,使用孩子兄弟表示法进行存储的结果如图所示:

由图我们可以发现,孩子兄弟表示法是用二叉树的左子树存储树的孩子结点,用右子树来存储兄弟结点。文章来源:https://www.toymoban.com/news/detail-617966.html
孩子兄弟表示法可以作为将普通树转化为二叉树的最有效的方法,同时这个方法也被称之为“二叉树表示法”或者”二叉链表表示法“文章来源地址https://www.toymoban.com/news/detail-617966.html
到了这里,关于数据结构:树的存储结构的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!