【图论】Prim算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了【图论】Prim算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一.介绍

【图论】Prim算法,图论,图论,算法

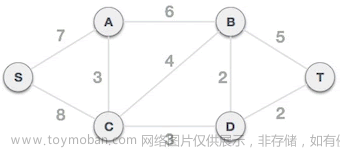
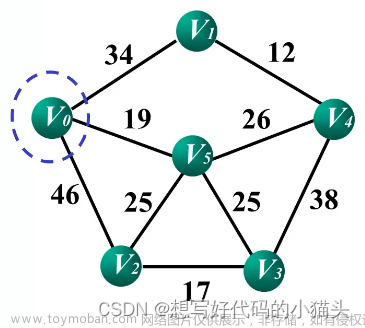
Prim算法是一种用于解决最小生成树问题的贪心算法。最小生成树问题是指在一个连通无向图中找到一个生成树，使得树中所有边的权重之和最小。

Prim算法的基本思想是从一个起始顶点开始，逐步扩展生成树，直到覆盖所有顶点。具体步骤如下：

选择一个起始顶点作为生成树的根节点，并将其加入生成树中。
从生成树中的顶点出发，选择一条与生成树相连的边中权重最小的边，并将其加入生成树中。
重复步骤2，直到生成树包含了所有顶点。

Prim算法的关键在于如何选择与生成树相连的边中权重最小的边。一种常用的方法是使用优先队列（最小堆）来存储候选边，每次选择权重最小的边加入生成树。

Prim算法的时间复杂度为O(ElogV)，其中V是顶点数，E是边数。它是一种有效的算法，适用于稠密图和稀疏图。

二.Prim与Dijkstra

其实Prim算法和Dijkstra算法差不多，就是一点小的改进，分别在第29，32，33行。

29：统计sum数量，若sum<n，说明无法构成最小树，因为构成最小树的点都不够！

32,33：w<dis[v]即可，因为只需要点到点，不是点到起点.

三.题目：

P3366 【模板】最小生成树 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)文章来源地址https://www.toymoban.com/news/detail-618230.html

四.【AC】代码

#include<bits/stdc++.h>
#define maxn 200005
#define inf 0x7fffffff
using namespace std;
int n,m,ans=0,sum=0;
int head[5001],dis[5001];
bool vis[maxn],flag=0;
//链式前向星
struct Edge{
	int u,v,w,next;
}edge[maxn<<1]; //无向图，要*2
int cnt=0;
void add(int u,int v,int w){
	edge[++cnt]=(Edge){u,v,w,head[u]};head[u]=cnt;
} 
struct node{
	int u,w;
	bool operator < (const node &x) const{return x.w<w;}
};
void Prim(){
	for(int i=2;i<=n;i++) dis[i]=inf;
	dis[1]=0;
	priority_queue<node> q;
	q.push((node){1,0});
	while(!q.empty()){
		node temp=q.top();q.pop();
		int u=temp.u;
		if(vis[u]) continue;
		vis[u]=1;sum++;ans+=temp.w;
		for(int i=head[u];i;i=edge[i].next){
			int v=edge[i].v,w=edge[i].w;
			if(w<dis[v]){
				dis[v]=w;
				q.push((node){v,dis[v]});
			}
		}
	}
}
int main(){
	//输入数据 
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v,w;cin>>u>>v>>w;add(u,v,w);add(v,u,w);
	}
	//调用算法 
	Prim();
	//输出答案
	if(sum==n) cout<<ans;
	else cout<<"orz"; 
	return 0;
}

到了这里，关于【图论】Prim算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！