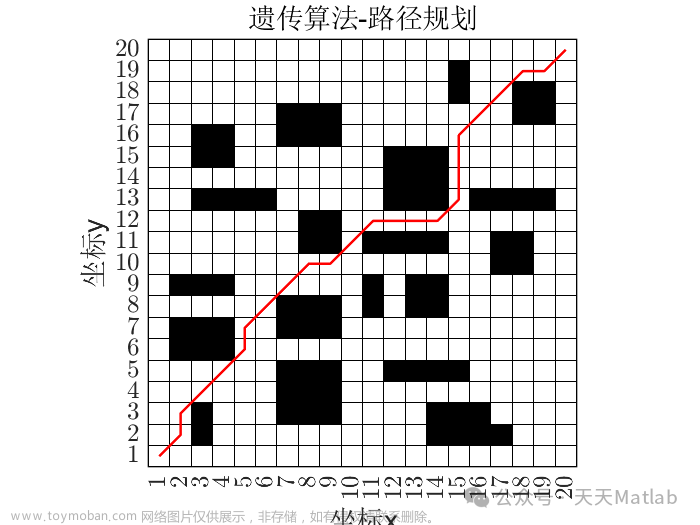
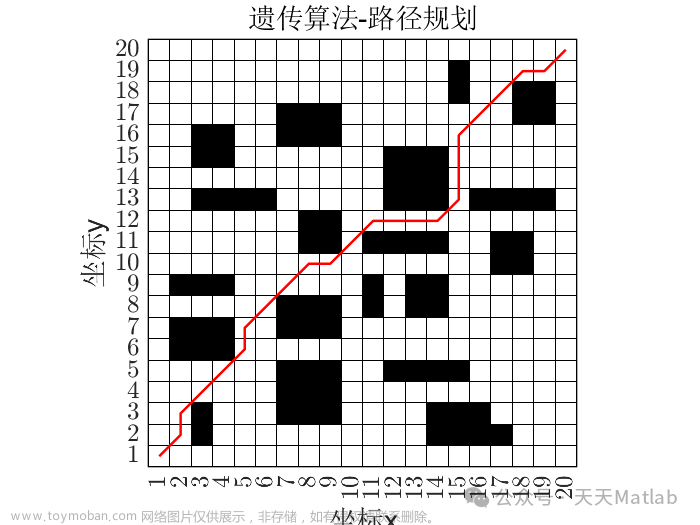
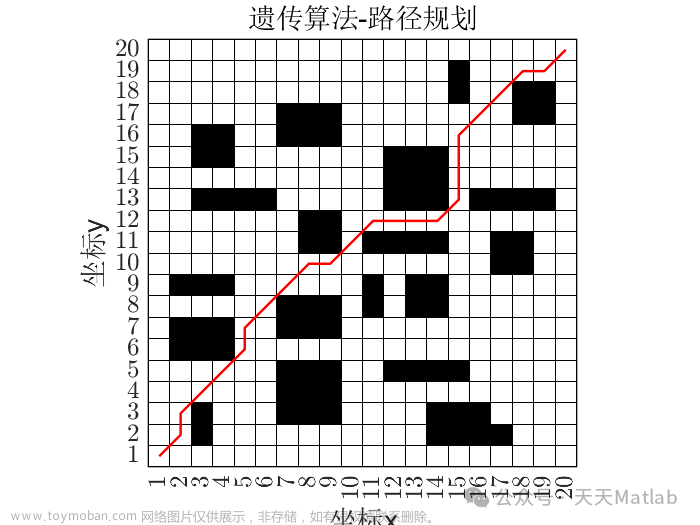
采用蚁群算法路径规划matlab
本文对基本蚁群算法代码进行了详细的注释,每一步都简单易懂。程序在matlab中可直接运行,适合刚开始学习本算法的同学入门。
蚁群算法是由意大利学者Dorigo提出的一种仿生智能算法,最早运用在旅行商问题上。蚁群算法模仿蚂蚁觅食过程设计出的智能启发式算法,蚂蚁觅食时在路径上释放信息素,后面的蚂蚁会被信息素含量多的路径吸引,进一步增加该路径上的信息素,从而形成正反馈,最终蚂蚁找到全局最优路径。文章来源:https://www.toymoban.com/news/detail-618290.html
环境建模
本文模仿机器人在二维空间的运动,所以采用使用最广泛地栅格法建立地图环境,将地图环境划分为N*N个网格,边长为1。白色网格代表机器人可行的网格,黑色网格代表障碍。将机器人看成一个质点,占据一个网格大小,机器人的移动按照八叉树的形式。为了存储路径的方便,如图采用序号法进行标记,从左到右分别是1、2、3,…,100。文章来源地址https://www.toymoban.com/news/detail-618290.html
代码实现
function main()
G=[0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0;
0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 1 1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0;
0 0 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 0 0 0;
0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0;
0 1 1 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0;
0 1 1 1 0 0 1 1 1 0 0 0 0 0 0 1 0 0 0 0;
0 1 1 1 0 0 0 1 1 1 0 0 0 1 0 1 0 0 0 0;
0 1 1 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0;
0 0 0 0 0 0 0 1 1 0 0 0 1 1 0 0 0 0 0 0;
0 0 0 0 1 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0;
0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 1 1 1 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 0;
0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0;
0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0;
0 0 0 0 0 0 1 0 0 1 1 1 0 0 0 0 0 1 1 0;
0 0 0 0 0 0 0 0 0 0 1 1 0 0 1 0 0 1 1 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0;
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;];
MM=size(G,1); % G 地形图为01矩阵,如果为1表示障碍物 ,size()返回矩阵G的行数,MM=20。如果size中的1改为2,则返回矩阵G的列数
Tau=ones(MM*MM,MM*MM); % Tau 初始信息素矩阵,规模为400*400,。记录每个栅格到其他栅格的信息素量。ones产生一个全是1的矩阵
Tau=8.*Tau; %矩阵全为8
K=50; %迭代次数(指蚂蚁出动多少波)
M=50; %蚂蚁个数
S=1; %最短路径的起始点,第一个栅格点为起始地,这里用1-400的序号代表点的位置,默认左上角是第一个
E=900; %最短路径的目的点
Alpha=1; % Alpha 表征信息素重要程度的参数
Beta=8; % Beta 表征启发式因子重要程度的参数
Rho=0.4; % Rho 信息素蒸发系数
Q=1; % Q 信息素增加强度系数
minkl=inf; %inf代表无穷大量
mink=0;
minl=0;
D=G2D(G); %G2D栅格矩阵转换成邻接矩阵的函数,D用于存储每个点到各自相邻无障碍栅格点的代价值(该点到其他点的可行性)
%若这两个节点在栅格地图中是自由栅格且是相邻或者对角的,则两点的距离则为邻接矩阵D的元素值,否则D的元素值为0
N=size(D,1); %N表示问题的规模(像素个数),N=400
a=1; %小方格像素的边长
Ex=a*(mod(E,MM)-0.5); %终止点横坐标,这一行E=-0.5。这是栅格地图的直角坐标表示法和序号表示法的映射关系。
if Ex==-0.5
Ex=MM-0.5; %这一行Ex=19.5
end
Ey=a*(MM+0.5-ceil(E/MM)); %终止点纵坐标,栅格地图的直角坐标表示法和序号表示法的映射关系。
Eta=zeros(N); %启发式信息矩阵,取为至目标点的直线距离的倒数,N=400,Eta大小为400*400
%以下启发式信息矩阵
%下面的for循环就是得到每个栅格点的坐标,并构建启发式信息矩阵(每个栅格点到目标点的距离)
for i=1:N
ix=a*(mod(i,MM)-0.5); %mod求i除以MM的余数
if ix==-0.5
ix=MM-0.5; %得到每一个栅格点的横坐标,一共400个
end
iy=a*(MM+0.5-ceil(i/MM)); %得到每一个栅格点的纵坐标,一共400个,这里ix,iy都是有400个元素的向量
if i~=E %~=不等号,E代表目标点这里是400
Eta(i)=1/((ix-Ex)^2+(iy-Ey)^2)^0.5;%计算该点到目标的距离长度,并输入到启发式信息矩阵Eta,一共400个
else
Eta(i)=100;
end
end
%到这里,步骤2完成
ROUTES=cell(K,M); %用细胞结构存储每一代的每一只蚂蚁的爬行路线。K迭代次数,M蚂蚁个数。cell类型每个单元可以储存任何数据
%把ROUTES初始化为一个K行M列的空cell类型数据
%比如ROUTES{1,1}=rand(5),就是ROUTES的1行1列的单元中存储的就是一个随机的5×5的方阵
PL=zeros(K,M); %用矩阵存储每一代的每一只蚂蚁的爬行路线长度
%启动K轮蚂蚁觅食活动,每轮派出M只蚂蚁
for k=1:K
for m=1:M
%状态初始化
W=S; %当前节点初始化为起始点,S=1是最短路径起始点,W用于表示当前所在节点
Path=S; %爬行路线初始化
PLkm=0; %爬行路线长度初始化
TABUkm=ones(N); %禁忌表初始化,N=400
TABUkm(S)=0; %已经在初始点了,因此要排除
DD=D; %邻接矩阵初始化,DD是400*400大小
%下一步可以前往的节点,蚂蚁走出第一步
DW=DD(W,:); %取行操作,取矩阵DD第W行的全部元素,矩阵DD的第一行代表第一个栅格点的邻接矩阵(也就是第一个栅格点能走的下一个点存储在第一行)
%第二行就是存储第二个栅格点到其他栅格点的可行性,DW大小是400*1
DW1=find(DW); %find函数,返回向量DW中非0元素的位置(就是非0元素是第几个数)
%DW1就得到了所以可以去的栅格点的序号,这样就筛选出当前可选择的点
for j=1:length(DW1)
if TABUkm(DW1(j))==0 %将可选择的点与禁忌表对比,如果这个点在禁忌表在是0,则这个点不能走
DW(DW1(j))=0; %更新这一行的邻接矩阵(蚂蚁当前所在点与其他所有点的邻接矩阵为W这一行),经过和禁忌表对比,如果不能走则更新为0
end
end
%到这里步骤3结束
LJD=find(DW); %找到经过与禁忌表对比以后还能选择的栅格点有哪些
Len_LJD=length(LJD);%可选节点的个数
%蚂蚁未遇到食物或者陷入死胡同(可选栅格点Len_LJD<1 )或者觅食停止
while W~=E&&Len_LJD>=1 %当前所在点不是目标点并且可选择节点数大于等于1,则进行下一步
%转轮赌法选择下一步怎么走
PP=zeros(Len_LJD); %得到可选节点数*可选节点数的0矩阵
for i=1:Len_LJD
PP(i)=(Tau(W,LJD(i))^Alpha)*((Eta(LJD(i)))^Beta); %概率选择公式的分子,PP(i)给矩阵第i个中的元素赋值
%Tau是信息素矩阵,W就是当前点,LJD(i)代表下一栅格点的位置(概率公式中的下标j)。Eta启发式信息矩阵
end
sumpp=sum(PP); %求概率公式的分母,将所有可访问栅格点的求和
PP=PP/sumpp; %建立概率分布,完整的概率公式
Pcum(1)=PP(1);
for i=2:Len_LJD
Pcum(i)=Pcum(i-1)+PP(i); %这个循环求所有路径概率的累加和
end
Select=find(Pcum>=rand); %Pcum是路径概率的累加和,来模仿各条路径对应轮盘扇面大小。rand是[0,1]之间的随机数
%find(Pcum>=rand)返回所有大于 rand 的扇面
to_visit=LJD(Select(1)); %选择第一个大于 rand 的扇面
%到这里步骤4结束
%状态更新和记录
Path=[Path,to_visit]; %路径增加,记录蚂蚁走的路径比如[1,3,5,10]从序号1走到序号3再走到序号5
PLkm=PLkm+DD(W,to_visit); %路径长度增加。知道起始点W和下一步走的点就可以在DD中找到两点的距离
W=to_visit; %蚂蚁移到下一个节点,把W定义为初始点,蚂蚁移动后初始节点也就变化了
for kk=1:N
if TABUkm(kk)==0 %禁忌表
DD(W,kk)=0; %DD是对称矩阵,禁忌表中0表示走过的或者不能走的栅格点,将走过的点在邻接矩阵中更新为0
DD(kk,W)=0; %根据禁忌表来更新邻接矩阵,因为蚂蚁走过一个点之后这个点不能走了吧,那么禁忌表中这个点就变了,那么下一步要走的点的邻接矩阵也变化了
end
end
TABUkm(W)=0; %已访问过的节点从禁忌表中删除(禁忌表大小应该是20*20)
%到这里步骤5结束
%开始第10代第20只蚂蚁的下一步
DW=DD(W,:);
DW1=find(DW);
for j=1:length(DW1)
if TABUkm(DW1(j))==0
DW(j)=0;
end
end
LJD=find(DW);
Len_LJD=length(LJD);%可选节点的个数
end
%while循环结束,第2代第3只蚂蚁走完这条路径
%记下每一代每一只蚂蚁的觅食路线和路线长度
ROUTES{k,m}=Path; %ROUTES是cell结构
if Path(end)==E %判断蚂蚁是否走到了终点,前面while循环中还有陷入死胡同的可能
PL(k,m)=PLkm; %PL矩阵存储每一代每一只蚂蚁的路径长度
if PLkm<minkl %步骤7中的与当前已知最短路径长度作比较,最开始mink1定义为无穷大的量(到这里我明白了这么定义的意义了)
mink=k;minl=m;minkl=PLkm; %mink存储蚂蚁代数,min1储存第几只蚂蚁,mink1储存最短路径长度
end
else
PL(k,m)=0;
end
end
%到这里一代的所有蚂蚁循环结束
%上面下面两部分是步骤8
%更新信息素,一代的所有蚂蚁完成一次路径搜索后按照公式更新信息素,这是全局信息素更新
Delta_Tau=zeros(N,N); %更新量初始化,N=400
for m=1:M %M=50代表蚂蚁个数
if PL(k,m) %PL(k,m)路径长度非0时条件成立(这条语句意味着到达目标终点了)
ROUT=ROUTES{k,m}; %这只蚂蚁走的路径给ROUT
TS=length(ROUT)-1; %跳数,意思就是蚂蚁从起始点到目标点跳了多少步,比如[1,4,12,9,10]跳了4步
PL_km=PL(k,m);
for s=1:TS
x=ROUT(s);
y=ROUT(s+1);
Delta_Tau(x,y)=Delta_Tau(x,y)+Q/PL_km; %信息素更新公式Q/蚂蚁K走的路径总长度PL_km
Delta_Tau(y,x)=Delta_Tau(y,x)+Q/PL_km; %上面的for循环,每一只蚂蚁走过路的都要更新信息素
end
end
end
%经过一次迭代,所有蚂蚁走完一次,更新信息素
Tau=(1-Rho).*Tau+Delta_Tau;%信息素挥发一部分,新增加一部分
end
%到这里所有代所有蚂蚁循环结束
%绘图
plotif=1;%是否绘图的控制参数
if plotif==1 %绘收敛曲线
minPL=zeros(K); %K=100
for i=1:K
PLK=PL(i,:); %PL路径长度,PL是k*m的矩阵
Nonzero=find(PLK); %PLK大小是1*m
PLKPLK=PLK(Nonzero); %PLKPLK储存第5代所有蚂蚁走的路径长度
minPL(i)=min(PLKPLK); %minPL中储存各代的最短路径长度,1*100
end
figure(1) %创建一个图像显示窗口
plot(minPL);
hold on %在当前图的轴(坐标系)中画了一幅图,再画另一幅图时,原来的图还在,与新图共存,都看得到
grid on %显示轴网格
title('收敛曲线变化趋势');
xlabel('迭代次数');
ylabel('最小路径长度'); %绘爬行图
figure(2)
axis([0,MM,0,MM]) %左下角为原点
for i=1:MM
for j=1:MM
if G(i,j)==1 %左上角是原点,如果该点是障碍
x1=j-1;y1=MM-i;
x2=j;y2=MM-i;
x3=j;y3=MM-i+1;
x4=j-1;y4=MM-i+1;
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]); %前两个是填充的范围,最后是填充的颜色
hold on
else %该点是空白点
x1=j-1;y1=MM-i;
x2=j;y2=MM-i;
x3=j;y3=MM-i+1;
x4=j-1;y4=MM-i+1;
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);
hold on
end
end
end
hold on
title('机器人运动轨迹');
xlabel('坐标x');
ylabel('坐标y');
ROUT=ROUTES{mink,minl}; %ROUT存放的是路径的索引序号不是点的坐标
LENROUT=length(ROUT);
Rx=ROUT;
Ry=ROUT;
for ii=1:LENROUT
Rx(ii)=a*(mod(ROUT(ii),MM)-0.5);
if Rx(ii)==-0.5
Rx(ii)=MM-0.5;
end
Ry(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));
end
plot(Rx,Ry)
end
plotif2=0;%绘各代蚂蚁爬行图
if plotif2==1
figure(3)
axis([0,MM,0,MM])
for i=1:MM
for j=1:MM
if G(i,j)==1
x1=j-1;y1=MM-i;
x2=j;y2=MM-i;
x3=j;y3=MM-i+1;
x4=j-1;y4=MM-i+1;
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[0.2,0.2,0.2]);
hold on
else
x1=j-1;y1=MM-i;
x2=j;y2=MM-i;
x3=j;y3=MM-i+1;
x4=j-1;y4=MM-i+1;
fill([x1,x2,x3,x4],[y1,y2,y3,y4],[1,1,1]);
hold on
end
end
end
for k=1:K
PLK=PL(k,:);
minPLK=min(PLK);
pos=find(PLK==minPLK);
m=pos(1);
ROUT=ROUTES{k,m};
LENROUT=length(ROUT);
Rx=ROUT;
Ry=ROUT;
for ii=1:LENROUT
Rx(ii)=a*(mod(ROUT(ii),MM)-0.5);
if Rx(ii)==-0.5
Rx(ii)=MM-0.5;
end
Ry(ii)=a*(MM+0.5-ceil(ROUT(ii)/MM));
end
plot(Rx,Ry)
hold on
end
end
%栅格地图转换成邻接矩阵的函数
function D=G2D(G)
l=size(G,1);
D=zeros(l*l,l*l);
for i=1:l
for j=1:l
if G(i,j)==0
for m=1:l
for n=1:l
if G(m,n)==0
im=abs(i-m);jn=abs(j-n);
if im+jn==1||(im==1&&jn==1)
D((i-1)*l+j,(m-1)*l+n)=(im+jn)^0.5;
end
end
end
end
end
end
end
到了这里,关于基于蚁群算法的机器人路径规划matlab——代码注释超级详细,都能看懂的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!