1003 Simple Set Problem
双指针的思想,双端队列
先从小到大排个序
一个一个放到双端队列里,一边放一边维护集合个数为k个
利用滑动窗口,当滑动窗口中集合个数为k时,只需算出滑动窗口最后一个数减去第一个数,然后每次取min就行了
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<deque>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef pair<int,int>PII;
const int N=1e6+10;
typedef pair<int,int>PII;
typedef long long ll;
int k,c;
int cnt[N];
void solve()
{
cin>>k;
int n=0;
vector<PII>ans;
for(int i=0;i<k;i++) cnt[i]=0;
for(int i=0;i<k;i++){
cin>>c;
n+=c;
while(c--){
int x;
cin>>x;
ans.push_back({x,i});
}
}
sort(ans.begin(),ans.end());
int sum=0;
int res=2e9;
deque<int>q;
for(int i=0;i<n;i++){
if(!cnt[ans[i].second]) sum++;
q.push_back(i);
cnt[ans[i].second]++;
if(sum<k) continue;
while(cnt[ans[q.front()].second]>1){
cnt[ans[q.front()].second]--;
q.pop_front();
}
res=min(res,ans[q.back()].first-ans[q.front()].first);
}
cout<<res<<endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}1006 PSO
两两组合
期望=所有组合的边数/组合数
组合数为中心节点与其它n-1个节点组合+在其它n-1个节点中选2个的组合(cnt)
所有组合的边数为n-1+2*cnt
当n大于2时,最大值均为2
另外,当n为2时,还需要特判,最大值为1
AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
//typedef pair<int,int>PII;
typedef long long ll;
ll n;
ll C2(ll x){
return x*(x-1)/2;
}
void solve()
{
cin>>n;
double res=((double)2*C2(n-1)+n-1)/(C2(n-1)+n-1);
printf("%.9lf ",res);
if(n==2) printf("%.9lf\n",1.0);
else printf("%.9lf\n",2.0);
}
int main()
{
// ios::sync_with_stdio(false);
// cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}1010 Kong Ming Qi
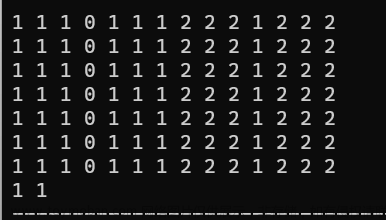
n*m和m*n是等价的,所以统一换成n小m大
当n为1时,答案明显为(m+1)/2
然后由一个基本图形(图1),可以吃掉连续三个棋子(如图4)

所以当n不是1时,我们都可以一直消掉3列
所以我们可以打表在一个范围里,当n和m很大时,都可以通过消掉3列,消掉3行来使得其落在打表范围里
当n等于5并且m等于5时,可以这么消

当n大于等于6,并且m大于等于6时,更加可以消3行3列
但是当n为4,m为5时,就只能消掉3列,行就不行了,所以当n和m都大于等于5时,才消3行3列,所以我们打表打到4*4

AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<deque>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
int ans[4][4]=
{
{1,1,2,2},
{1,1,2,1},
{2,2,2,2},
{2,1,2,1}
};
void solve()
{
int n,m;
cin>>n>>m;
if(n>m) swap(n,m);
if(n==1){
cout<<(m+1)/2;
return;
}
while(n>=5) n-=3;
while(m>=5) m-=3;
cout<<ans[n-1][m-1]<<endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}1011 circuit
floyd算法求最小环问题
floyd算法求最短路原理:

得到以下状态转移方程

然后可以将最高维k去掉,因为第一维时一层一层算上去的,第k层只需要用到它的上一层,即k-1层,不用前面的其它层,那么只用从1到n的循环,然后一层一层上去就行了,完全可以删掉第一维
于是转化成了d[i][j]=d[i][k]+d[k][j]
对于i->j,最短路径是经过不超过k的中间节点,d[i][j]是由不超过k的中间节点更新的最短距离
所以当枚举到k时,枚举小于k的节点,并判断是否与k相邻,然后再判断是否是环,这样的话这个环上的所有节点都不超过k,这样才能不重不漏
另外,枚举到某个k时,此时更新的最短距离是由小于等于k的中间节点更新的,所以此时去判断a[k][i]+dist[i][k]<mn(i从1到k-1)用到的dist[i][k]才会准确
关于为什么不能重新在外面写一个k从1到n的循环,将判断环的部分放在这个循环里:
首先我们不重不漏地枚举两个点,方法是对于编号为k的节点,我们只枚举编号比它小的节点(即1到k-1),然后如果两个点相邻,即k->i有一条边,那么我们就看k->i的权值加上i到k的最短距离是不是正无穷,如果不是,那么说明有环
但是我们枚举环的时候也得做到不重不漏,如下图所示:
当k为3时,我们会找到比它小的编号1,发现3->1有一条边,然后我们会算3->1的边权值加上1到3的最短距离是不是正无穷,发现不是,那么就是一个环,但是呢,我们只能找由2更新1到3的最短距离的这个环,不能找由4更新1到3的最短距离的这个环,不然的话,当我们枚举到k为4时,又会找到4->3这条边,会再次找到4->3->1这个环,那么同样的环就找到了两次
所以我们只能找由编号小于等于k的节点更新的最短距离,而这刚好和floyd算法相符,当枚举到k时,更新的最短距离都是由小于等于k的中间节点更新的,所以每枚举一次k,我们就找一次环

AC代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
#include<queue>
#include<cmath>
#include<cstdio>
#define endl '\n'
//#define int long long
using namespace std;
typedef long long ll;
const int N=510,mod=998244353;
const ll INF=1e18;
int a[N][N];//a[i][j]表示i和j边权值
ll dist[N][N];//dist[i][j]表示i和j之间的最短距离
int cnt[N][N];//cnt[i][j]表示i和j之间的最短路的数量
int n,m;
void solve() {
cin>>n>>m;
//将自环距离初始化为0,其它初始化为INF
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++) {
a[i][j]=0,dist[i][j]=INF;
}
}
for(int i=1; i<=n; i++) dist[i][i]=0;
for(int i=0; i<m; i++) {
int x,y,z;
cin>>x>>y>>z;
a[x][y]=z;
dist[x][y]=z;
cnt[x][y]=1;
}
ll mn=INF;
ll count=0;
for(int k=1; k<=n; k++) {
for(int i=1; i<=n; i++) {
for(int j=1; j<=n; j++) {
if(dist[i][j]>dist[i][k]+dist[k][j]) {
dist[i][j]=dist[i][k]+dist[k][j];
cnt[i][j]=1ll*cnt[i][k]*cnt[k][j]%mod;
} else if(dist[i][j]==dist[i][k]+dist[k][j]) {
cnt[i][j]=(cnt[i][j]+1ll*cnt[i][k]*cnt[k][j])%mod;
}
}
}
for(int i=1; i<=k-1; i++) {
if(a[k][i]) {
if(a[k][i]+dist[i][k]<mn) {
mn=a[k][i]+dist[i][k];
count=cnt[i][k];
} else if(a[k][i]+dist[i][k]==mn) {
count=(count+cnt[i][k])%mod;
}
}
}
}
if(mn==INF) mn=-1,count=-1;
cout<<mn<<" "<<count<<endl;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}1012 a-b Problem
对于每一个ai,bi,求它们的和,然后从大到小排序,依次取
原因在于自己取了其中一个,对方没有取另一个,那么自己比对方就多了两者之和文章来源:https://www.toymoban.com/news/detail-618418.html
AC代码:文章来源地址https://www.toymoban.com/news/detail-618418.html
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#define endl '\n'
//#define int long long
using namespace std;
const int N=1e5+10;
//typedef pair<int,int>PII;
typedef long long ll;
ll n;
struct node{
ll a;
ll b;
ll sum;
bool operator<(const node &W)const{
return sum>W.sum;
}
}ans[N];
void solve()
{
cin>>n;
for(int i=1;i<=n;i++){
cin>>ans[i].a>>ans[i].b;
ans[i].sum=ans[i].a+ans[i].b;
}
sort(ans+1,ans+1+n);
ll sum1=0,sum2=0;
for(int i=1;i<=n;i++){
if(i%2==1) sum1+=ans[i].a;
else sum2+=ans[i].b;
}
cout<<sum1-sum2<<endl;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t=1;
cin>>t;
while(t--)
solve();
return 0;
}到了这里,关于(杭电多校)2023“钉耙编程”中国大学生算法设计超级联赛(4)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!