- 练习
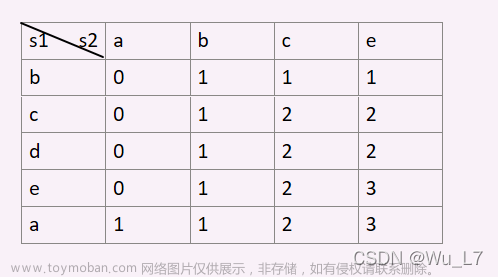
给出2个小写字母组成的字符串,求它们最长的公共子串的长度是多少?
例如:”abcdefg” 与”xydoeagab”。有最长的公共子串”deg”,
答案为:3。
输入格式
第一行:一个字符串,长度不超过1000。
第二行:一个字符串,长度不超过1000。
输出格式
输出一个整数。
输入/输出例子1
输入:
edabcdfg
kdxbcafbg
输出:
5
样例解释
无文章来源地址https://www.toymoban.com/news/detail-618507.html
代码:
#include<bits/stdc++.h>
using namespace std;
string a,b;
int f[1004][1004];
int ans;
int dp();
int main(){
cin>>a>>b;
for(int i = 0;i < a.size();i++)
for(int j = 0;j < b.size();j++){
int maxLen = 0;
if(a[i] == b[j]){
if(i > 0&&j > 0)maxLen = 1+(f[i-1][j-1]);
else maxLen = 1;
}else{
if(i > 0)maxLen = max(maxLen,f[i-1][j]);
if(j > 0)maxLen = max(maxLen,f[i][j-1]);
}
f[i][j] = maxLen;
}
cout<<f[a.size()-1][b.size()-1]<<endl;
return 0;
}- 测试
有个helihui建造的通道,这个通道比较奇怪,我们把通道看成平面的,里面全是数字,

走的时候只能一格一格的走,走的方向只能往下或往右,并且不能走出边界。从入口进来,每个格子代表通过这个格子的时间。Helihui规定最左上角是通道入口, 最右下角是通道出口,现在要求你判断从入口到出口的所有路径中总时间最小的那条路径。并输出通过该条路径的总时间,上面的红色箭头是表示这样走可以得到最小的总时间。
输入格式
输入数据有多组。
每组输入n,m整数,n表示通道格子的行数,m表示通道格子的列数,0<=n,m<=100,接下来输入n行m列的矩阵,矩阵的数据的范围0到32765。
走的时候从通道入口进入从出口出去,并且通道入口一直在最左上角,通道出口一直在最右下角。
输出格式
输出从入口到出口所有路径中最短时间。
输入/输出例子1
输入:
4 6
3 4 3 2 5 2
1 6 7 5 3 1
2 1 8 6 9 1
7 10 4 6 7 8
输出:
29
样例解释
无
代码:
#include <bits/stdc++.h>
using namespace std;
int tt[110][110];
int dp[110][110];
int main()
{
int n, m;
while(~scanf("%d%d",&n,&m))
{
memset(tt, 0, sizeof(tt));
for(int i = 1; i <= n; i ++)
{
for(int j = 1; j <= m; j ++)
{
scanf("%d",&tt[i][j]);
//dp[i][j] = 9999999;
}
}
for(int i = 0; i <= 110; i ++)
{
for(int j = 0; j <= 110; j ++)
{
dp[i][j] = 99999990;
}
}
for(int i = 1; i <= m; i ++)
{
tt[1][i] += tt[1][i - 1];
dp[1][i] = tt[1][i];
}
for(int i = 2; i <= n; i ++)
{
for(int j = 1; j <= m; j ++)
{
dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + tt[i][j];
}
}
printf("%d\n",dp[n][m]);
}
}对于从1到N的连续整集合合,能划分成两个子集合,且保证每个集合的数字和是相等的。举个例子,如果N=3,对于{1,2,3}能划分成两个子集合,他们每个的所有数字和是相等的:
{3} and {1,2}
这是唯一一种分法(交换集合位置被认为是同一种划分方案,因此不会增加划分方案总数)
如果N=7,有四种方法能划分集合{1,2,3,4,5,6,7},每一种分发的子集合各数字和是相等的:
{1,6,7} and {2,3,4,5} {注:1+6+7=2+3+4+5}
{2,5,7} and {1,3,4,6}
{3,4,7} and {1,2,5,6}
{1,2,4,7} and {3,5,6}
给出N,你的程序应该输出划分方案总数,如果不存在这样的划分方案,则输出0。
输入格式
输入文件只有一行,且只有一个整数N(N<=39)
输出格式
输出划分方案总数,如果不存在则输出0。
输入/输出例子1
输入:
7
输出:
4
样例解释
无
代码:
#include<bits/stdc++.h>
using namespace std;
int main(){
long long dyn[100000];
memset(dyn,0,100);
long long n,s;
cin>>n;
s=n*(n+1);
if(s%4)
{
cout<<0<<endl;
}
s/=4;
long long i,j;
dyn[0]=1;
for(i=1;i<=n;i++)
{
for(j=s;j>=i;j--)
dyn[j]+=dyn[j-i];
}
cout<<dyn[s]/2<<endl;
return 0;
}搬寝室时xhd看着寝室里的n件物品开始发呆,因为实在是太多了,于是xhd决定随便搬2*k件过去就行了.幸运的是xhd根据多年的搬东西的经验发现每搬一次的疲劳度是和左右手的物品的重量差的平方成正比(这里补充一句,xhd每次搬两件东西,左手一件右手一件).例如xhd左手拿重量为3的物品,右手拿重量为6的物品,则他搬完这次的疲劳度为(6-3)^2 = 9.现在可怜的xhd希望知道搬完这2*k件物品后的最佳状态是怎样的(也就是最低的疲劳度)。
输入格式
每组输入数据有两行,第一行有两个数n,k(2<=2*k<=n<=2000).第二行有n个整数分别表示n件物品的重量(重量是一个小于2^15的正整数).
输出格式
对应每组输入数据,输出数据只有一个表示他的最少的疲劳度,每个一行.
输入/输出例子1
输入:
2 1
1 3
输出:
4
代码
#include<iostream>
#include<algorithm>
#define F 0x7fffffff
using namespace std;
long long dp[2000][2000];
long long wei[200000];
int main()
{
long long n,m;
while(cin>>n>>m)
{
for(long long i=1;i<=n;i++)
cin>>wei[i];
sort(wei+1,wei+n+1);
for(long long i=1;i<=n;i++)
for(long long j=1;j<=n;j++)
dp[i][j]=F;
for(long long i=2;i<=n;i++)
for(long long j=1;j*2<=i;j++)
dp[i][j]=min(dp[i-1][j],dp[i-2][j-1]+(wei[i]-wei[i-1])*(wei[i]-wei[i-1])) ;
cout<<dp[n][m]<<endl;
}
return 0;
}有一个炸弹被敌人设置了密码,现在要求你来破解这个密码!已知密码是由N个数字组成的,并且密码是用下图所示的面板设置的,还知道敌人设置的密码中任意相邻的两个数字在面板中的按键也是相邻的(也就是说两个按键有公共边)。

为了估计大概破解的时间,现在任务是要求你计算一下,敌人设置的密码有多少种不同的可能?
输入格式
一个整数N, 2 <= N <= 30
输出格式
一个整数,密码有多少种不同的可能.
输入/输出例子1
输入:
2
输出:
26
输入/输出例子2
输入:
25
输出:
768478331222文章来源:https://www.toymoban.com/news/detail-618507.html
样例解释
无
#include<bits/stdc++.h>
using namespace std;
const int dx[4]={-1,1,0,0};
const int dy[4]={0,0,-1,1};
int n;
long long ans;
int a[5][5];
long long f[50][20];
int main(){
cin>>n;
for(int i = 1;i <= 3;++i){
for(int j = 1;j <= 3;++j){
a[i][j] = (i-1)*3+j;
}
}
a[4][1] = 0;a[4][2] = a[4][3]= -1;
for(int i = 0;i < 10;++i) f[1][i] = 1;
for(int i = 2;i <= n;++i)
for(int j = 0;j < 10;++j){
int x = (j-1)/3+1,y = (j-1)%3+1;
if(j == 0)x=4,y=1;
for(int k = 0;k < 4;++k){
int nx = x+dx[k],ny = y+dy[k];
if(nx<1||ny<1||nx>4||ny>3||a[nx][ny]==-1)continue;
f[i][j]+=f[i-1][a[nx][ny]];
}
}
for(int i = 0;i < 10;++i)ans+=f[n][i];
cout<<ans;
return 0;
}到了这里,关于动态规划入门第4课,经典DP问题3 ----公共最长子序列的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!