LeetCode使用最小花费爬楼梯（动态规划）-Toy模板网

这篇具有很好参考价值的文章主要介绍了LeetCode使用最小花费爬楼梯（动态规划）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

链接: 使用最小花费爬楼梯

题目描述

LeetCode使用最小花费爬楼梯（动态规划）,leetcode,动态规划,算法

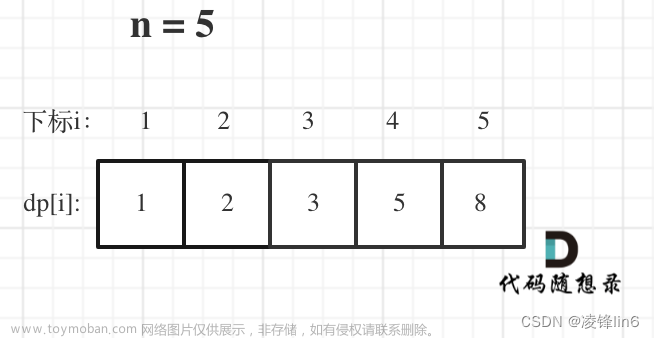
算法流程(方法一)

LeetCode使用最小花费爬楼梯（动态规划）,leetcode,动态规划,算法

编程代码

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        size_t size = cost.size()  + 1;
        vector<int> dp(size);
        dp[0] = dp[1] = 0;
        for(int i = 2;i < size;++i)
        {
            dp[i] = min(dp[i-2]+cost[i-2],dp[i-1]+cost[i-1]);
        }
        return dp[size-1];
    } 
};

LeetCode使用最小花费爬楼梯（动态规划）,leetcode,动态规划,算法

优化代码

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        size_t size = cost.size()  + 1;
        int a,b,c,d;
        a = b = 0;

        for(int i = 2;i < size;++i)
        {
            c = min(a+cost[i-2],b+cost[i-1]);
            a = b;
            b = c;
        }
        return c;
    } 
};

LeetCode使用最小花费爬楼梯（动态规划）,leetcode,动态规划,算法

算法流程（方法二）

LeetCode使用最小花费爬楼梯（动态规划）,leetcode,动态规划,算法

编程代码

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        size_t n = cost.size();
        vector<int>vv(n);
        vv[n-1] = cost[n-1];
        vv[n-2] = cost[n-2];

        for(int i = n-3;i >= 0;--i)
        {
            vv[i] = min(vv[i+1],vv[i+2])+cost[i];
        }
        return min(vv[0],vv[1]);
    } 
};

LeetCode使用最小花费爬楼梯（动态规划）,leetcode,动态规划,算法文章来源地址https://www.toymoban.com/news/detail-618653.html

代码优化

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        size_t n = cost.size();
        int a = cost[n-1];
        int b = cost[n-2];
        int c;
        for(int i = n-3;i >= 0;--i)
        {
            c = min(a,b)+cost[i];
            a = b;
            b = c;
        }
        return min(a,b);
    } 
};