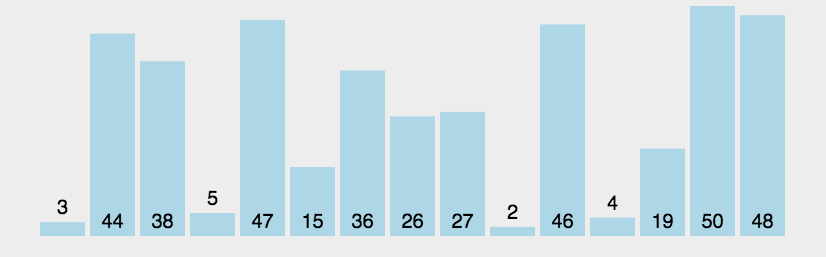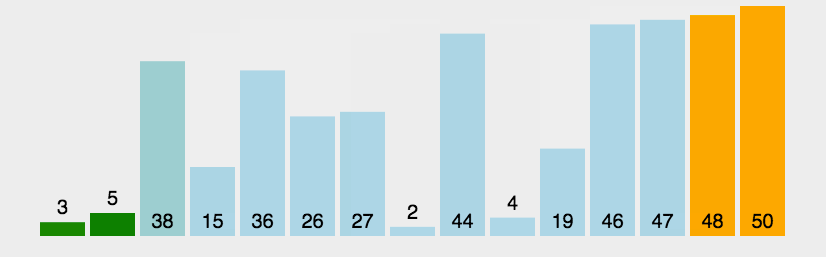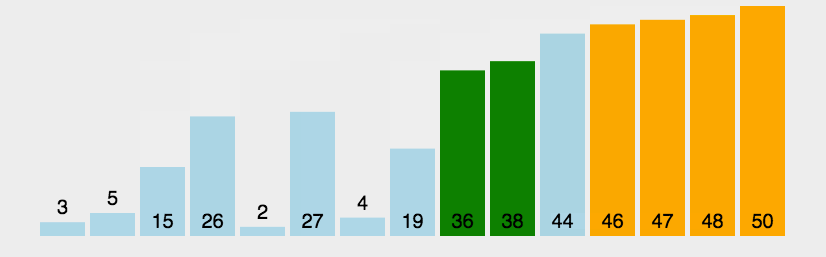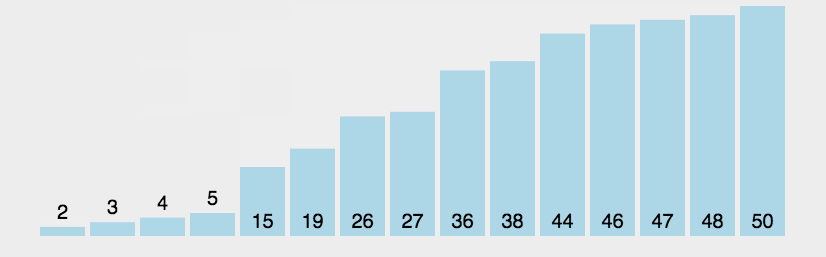距离上次更新已经很久了,以前都是非常认真的写笔记进行知识分享,但是带来的情况并不是很好,一度认为发博客是没有意义的,但是这几天想了很多,已经失去了当时写博客的初心了,但是我觉得应该做点有意义的事,将知识分享给那些乐于学习想钻研的同学,我们可以一起学习,一起进步,所以想出以个系列(算法篇),将我学习算法的过程记录下来,一起加油!!!废话不多说,看正片
1. 概念:
选择排序(Selection sort)是一种简单直观的排序算法,由于是选择,所以在交换的过程中元素的相对位置可能会发生变换,所以该算法是不稳定排序。
选择排序中的关键在于,怎么找出一堆数据中最小(最大)的,和冒泡排序相比,选择排序比冒泡排序的效率高,高在交换位置的次数上,选择排序的交换位置是有意义的交换,每次遍历剩下的元素找到最小值(最大值),拿到这个最值与最前面的元素进行交换

举个栗子:假如我们现在需要给一个数组进行排序[3,2,5,9,4];
第一次参与比较的数据:3 2 5 9 4(最前面的元素索引为0,所以找到最小的元素和索引为0的元素进行交换)
最小值:3 2 5 9 4-->2
所以交换完数组中变为2 3 5 9 4
第二次参与比较的数据3 5 9 4(最前面的索引为1)
最小值:3 5 9 4
所以交换为数组变为3 5 9 4(因为本身索引为1的元素就是数组中元素最小的,所以不需要进行交换位置)
依次类推...
最后排好序的数组是[2,3,4,5,9]
具体实现:使用双重循环,外层循环控制比较的次数,内循环找出每次比较数据中的最小值,然后将其放入已排序的末尾
public void selection(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
for (int i = 0; i < arr.length - 1; i++) { // 寻找的次数
// 假设i的位置就是数组中未排序元素值中最小值的位置
int minIndex = i;
for (int j = i + 1; j < arr.length; j++) { // 与后面的元素进行比较
if (arr[minIndex] > arr[j]) {
minIndex = j;
}
}
// 若最小值不等于当前i,则进行交换
if (minIndex != i) {
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
}2.leetcode题单
学会选择排序,我们可以顺便解决leetcode上的这些题:
颜色分类
寻找两个正序数组的中位数
至少是其他数字两倍的最大数文章来源:https://www.toymoban.com/news/detail-619395.html
判断能否形成等差数列文章来源地址https://www.toymoban.com/news/detail-619395.html
颜色分类:
class Solution {
public void sortColors(int[] nums) {
if (nums == null || nums.length == 0) {
return;
}
//计数排序
int max=Arrays.stream(nums).max().getAsInt();
int[] hash=new int[max+1];
for (int i = 0; i <nums.length; i++) {
hash[nums[i]]++;
}
int index=0;
for (int i = 0; i <hash.length; i++) {
int n=hash[i];
while(n!=0){
nums[index++]=i;
n--;
}
}
}
}寻找两个正序数组的中位数
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
if (nums1 == null && nums2 == null) {
return 0;
}
//将两个数组合并成一个数组然后取中间值
int[] sortNum = new int[nums1.length + nums2.length];
int q = sortNum.length;
;
int i = 0;
int j = 0;
int k = 0;
int m = nums1.length;
;
int n = nums2.length;
while (i < m && j < n) {
if (nums1[i] < nums2[j]) {
sortNum[k++] = nums1[i++];
} else {
sortNum[k++] = nums2[j++];
}
}
while (i < m) {
sortNum[k++] = nums1[i++];
}
while (j < n) {
sortNum[k++] = nums2[j++];
}
//数组分为奇数和偶数
if((q&1)==1){
return sortNum[q/2];
}else{
return (sortNum[q/2]+sortNum[(q/2)-1])/2.0;
}
}
}至少是其他数字两倍大的数字
class Solution {
public int dominantIndex(int[] nums) {
if (nums == null) {
return 0;
}
int max=nums[0];
int maxIndex = 0;
for (int i = 1; i < nums.length; i++) {
if(nums[i]>max){
max=nums[i];
maxIndex=i;
}
}
Arrays.sort(nums);
if (nums[nums.length - 1] >= 2 * nums[nums.length - 2]) {
return maxIndex;
}else{
return -1;
}
}
}判断能否形成等差数列
class Solution {
public boolean canMakeArithmeticProgression(int[] arr) {
if(arr==null||arr.length==0){
return false;
}
Arrays.sort(arr);
int k=arr[1]-arr[0];
for (int i =1; i <arr.length; i++) {
if(arr[i]-arr[i-1]!=k){
return false;
}
}
return true;
}
}到了这里,关于一起学算法(选择排序篇)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!