C++时间复杂度详解-Toy模板网

这篇具有很好参考价值的文章主要介绍了C++时间复杂度详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一般时间复杂度的表现形式是大O表示法，即O( )。

大O表示法有以下4条法则：

1.括号中所有常数加数省略，如只有一个常数，记为1。如O(372+n)→O(n)、O(89)→O(1)。

2.括号中去掉所有常数乘数如O(2n)→O(n)、O(3n+n+45*2)→O(4n+90)→O(4n)→O(n)。

3.括号中的数是整个代码每个操作次数的总和

4.括号中指数和底数都不能省略

用大O表示法出现较为频繁有以下8种，从快到慢排序为：

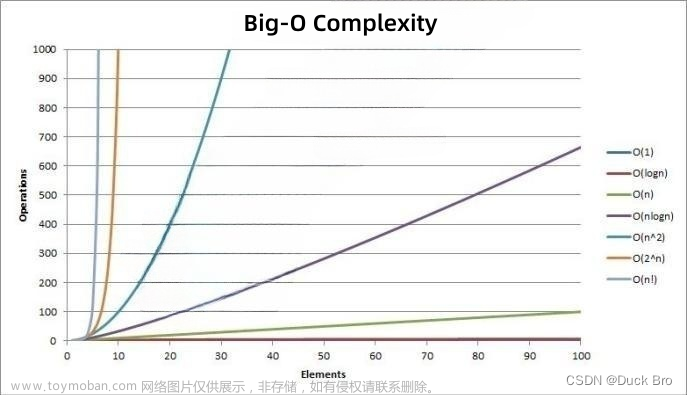
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2^n)<O(n!)

即：

这里借鉴了一下CSDN苏禾呀的图片。

下面找几种常用的解释：

O(1) [常数阶]

int main() {
    int x;//1次
    cin>>x;//1次
    for(int i=1;i<=231;i++)    
        x*=x;//231次(注意，出现循环不一定是O(n),而要根据操作次数来判断)
    cout<<x;//1次
    return 0//1次
}

上面的主函数时间复杂度为O(1+1+231+1+1)，根据上面的计算法则，

O(1+1+231+1+1)

=O(235)

=O(1)

O(n) [线性阶]

int main() {
    int n;   //1次
    cin>>n;   //1次
    n*=1024;   //1次
    for(int i=1;i<=n;i++)
        cout<<i<<endl;   //n*1024次
    while(n--) {
        cout<<n<<endl;       //n*1024次
    }
    return 0;   //1次
}

上面的主函数时间复杂度为O(1+1+1+n*1024*2+1),根据上面的计算法则，

O(1+1+1+n*1024*2+1)

=O(1*4+2048*n)

=O(2048*n)

=O(n)

O(logn) [对数阶]

int main() {
    int i,n;   //1次
    cin>>n;   //1次
    while（i<n） {
        i*=2;//log n次
        cout<<"hello world!";   //log n次
    }
    return 0;   //1次
}

上面的主函数时间复杂度为O(1+1+1+logn*2),根据上面的计算法则，

O(1+1+1+logn*2)

=O(logn*2)

=O(logn)

注意：

logn 表示求 2的几次方等于n,著名的二分折半查找的时间复杂度就是O(logn)。

O(n^2) [平方阶]

int main() {
    int n;   //1次
    cin>>n;   //1次
    for(int i=1;i<=n;i++) {
        for(int j=1;j<=n;j++)
            cout<<"dhuheidhushgfgirfiowgrgougrugubo";   //n*n次
    }
    return 0;   //1次
}

上面的主函数时间复杂度为O(1+1+1+n*n),根据上面的计算法则，

O(1+1+1+n*n)

=O(n*n)

=O(n^2)

在这里：

循环输出的操作次数为n^2次，因为外层循环操作了n次，而每一次外层循环时，又要做n次内层循环，根据乘法原理，得到总操作数为n*n。

另

在遇到if-else 时，其操作次数应以较多次数为结果。

例如：

int main() {
    int n,k;
    cin>>n>>k;
    if(k==1) {
        for(int i=1;i<=n;i++) 
            cout<<i<<endl;    //n次
    }else cout<<"hello!";   //1次
    return 0;
}

在上面的选择语句一条分支为n，一条分支为1。O(n)>O(1),所以选择语句的时间复杂度为O(n)。文章来源地址https://www.toymoban.com/news/detail-619665.html