线性代数的学习和整理2：线性代数的基础知识(整理ing)

目录

1 写在前面的话

1.1 为什么要先总结一些EXCEL计算矩阵的工具性知识， 而不是一开始就从基础学起呢？

 1.2 关于线性代数入门时的各种灵魂发问：

1.3 学习资料

2 什么是线性(关系)？

2.1 线性的到底是一种什么关系：

线性关系=正比例/正相关关系 ≠ 直线型关系

2.2 一次函数的只是一种 直线性关系

2.3 线性的严格定义

2.4 向量和矩阵的平直概念（也是线性关系的另一种说法：图形上是直线，不能是2次函数，或指数函数等等）

3   从函数的角度看线性

3.1 一些函数的定义回顾

3.2 函数与几何图形的对应

3.3 一次函数和线性函数 不是一回事

3.3.1 一次函数：形如如 y=ax+b  或  z=ax+by+c

3.3.2 特殊一次函数：形如y=ax 或 z=ax+by

3.4 函数和矩阵的联系

3.4.1 函数和矩阵

3.4.2 函数方程组 和 矩阵

3.5 某种意义上说，这就是线性代数的本质？

4 线性相关在向量/矩阵里的作用和应用

4.1 线性相关

4.2 线性相关的严格定义

4.2.1 直观的感觉

4.2.2 原始严格定义1（更直观：1个向量与多个其他向量的关系）

4.2.3 严格定义2 （把 所有要比较的向量看作一个整体）

4.2.4  线性相关的几何意义

2维向量之间线性相关

多个3维向量之间的线性相关的几何关系就不好想象了

4.3 线性组合的意思

4.3.1 线性组合的具体方法

4.4 线性变换(可以线性变换的矩阵之间是等价矩阵)

4.4.1 线性变换内容

4.4.2 线性变换的作用举例（作用很多，很大）

4.5 线性变换（线性映射）的意义？

4.6 线性相关的其他意义

5 线性无关/线性独立

5.1  线性无关的定义

5.2 线性无关有什么用呢？

6 线性代数的本质

6.1 线性代数和普通代数的区别

6.2 某种意义上说，这就是线性代数的本质？

6.3 对应到EXCEL的操作，EXCEL的数组公式= 线性代数计算

6.4 线性代数的核心是什么

6.5 线性代数是人造的，还是自然的？

1 写在前面的话

1.1 为什么要先总结一些EXCEL计算矩阵的工具性知识， 而不是一开始就从基础学起呢？

      还是那个老问题和老答案：虽然一般的学习路径是需要先了解基础知识才能运用。但是我觉得先能用到觉得有用，然后再去提问，这样的反馈循环能促进人的学习，我更适合后者，能用到了再回过头来学习更好

     另外，上学时是学过线代的，但是现在全忘了，还是因为没有理解导致的，这次尽量能先学懂，再考虑去学习各自计算技巧，多去思考和理解线性代数的本质，而不是只会算几个题而已，那样过段时间还是会忘。

    最后：最大的原因，直接这么找一本书埋头学，不以应用的目的去学，我可能早放弃了

 1.2 关于线性代数入门时的各种灵魂发问：

1. 什么是线性
2. 什么是线性相关 ？
3. 为什么叫线性变换？
4. 为什么叫线性代数？

     其实回答这些问题，还是会者不难，难者不会，但是对初学者理清概念非常重要。

     学一门课的时候知道它在干啥为什么要研究这些问题真的很重要，虽然这些问题需要深度学习后才能有较深的理解，但是我试着开头就回答下这些问题，以后可以逐步来修改，毕竟，这是学习笔记而已。

1.3 学习资料

• 能看知乎，别看百度，能看B站，别看知乎
• 百度写的你看不懂，
• 知乎写的很可能都是片段

麻省理工学院 - MIT - 线性代数（我愿称之为线性代数教程天花板）_哔哩哔哩_bilibili麻省理工学院 - MIT - 线性代数（我愿称之为线性代数教程天花板）共计35条视频，包括：1.01方程组的几何解释、2.02矩阵消元、3.03乘法和逆矩阵等，UP主更多精彩视频，请关注UP账号。https://www.bilibili.com/video/BV16Z4y1U7oU/?spm_id_from=333.337.search-card.all.click

3bule1brown的视频，B站有原作者自己发的视频，有多牛逼就不用我说了

【熟肉】线性代数的本质 - 00 - “线性代数的本质”系列预览_哔哩哔哩_bilibili线性代数的本质（Essense of Linear Algebra）系列作者：@3Blue1Brown ( https://www.youtube.com/channel/UCYO_jab_esuFRV4b17AJtAw )视频源地址：https://www.youtube.com/watch?v=kjBOesZCoqc听译、时间轴、压制：@Solara57000 - “线性代数的本质”系列的简介, 视频播放量 392850、弹幕量 579、点赞数 10225、投硬币枚数 7107、收藏人数 18635、转发人数 9114, 视频作者 3Blue1Brown, 作者简介 中国官方账号。深入浅出、直观明了地分享数学之美。资助页面：www.patreon.com/3blue1brown，相关视频：【熟肉】线性代数的本质 - 01 - 向量究竟是什么？，【数学漫步之旅】看点1：证明“证明”的本身 竖版，【纪录片】数学漫步之旅 01 本福特定律，【纪录片】数学漫步之旅 02 无穷小微积分，【23考研】线代非李永乐不可吗？跟其他老师，我的线代考砸了| 听课与做题| 规划与建议，【搬运】【线性代数】线性代数的本质，矩阵的秩--直观解释，【熟肉】线性代数的本质 - 03 - 矩阵与线性变换，考研数学线性代数老师推荐，现在看到还不晚！，考研线代可以选张宇老师吗？https://www.bilibili.com/video/BV1rs411k7ru/?spm_id_from=333.999.0.0&vd_source=5fa6d2958ae880d9550a17f8050fd5ed其他书

• MIT《introduction to linear algebra》
• 《线性代数应该这样学》
• 《程序员的数学，线性代数》
• 《马同学图解线性代数》
• 《线性代数及其应用》
• 《线性代数的几何意义》
• 《简明线性代数》

2 什么是线性(关系)？

• 最直观的回答是：直线型？长的像直线的就是线性关系
• 图形上，形如直线的就是线性？
• 那从函数形式上看呢？ y=Ax是吗？  y=Ax+b 是吗？
• 这些说法对吗？

2.1 线性的到底是一种什么关系：

线性关系=正比例/正相关关系 ≠ 直线型关系

线性，指量与量之间按比例、成直线的关系，在空间和时间上代表规则和光滑的运动；而非线性则指不按比例、不成直线的关系，代表不规则的运动和突变。

什么是线性呢？文字定义

• 是一种正比例关系，正相关关系
• 是一种，自变量（输入内容）按比例变化，因变量（输出内容）按相同比例变化的关系
• 而不是只是直线性关系就是线性关系，直线性关系还不够
• 所以y=ax 是线性关系
• 而y=ax+b 只是直线性关系，不是线性关系

反例：非线性

比较，确实不是正比例

• y1=F1(x)=ax
• y2=F2(x)=ax+b

从其他学科的角度看：非线性就表示输入输出不是一种正比例关系

• 比如y看成是输出，x看成是输入
• 把函数  y=F(x)=ax+b ，显然y和x不是正比例关系
• 而函数  y=F(x)=ax，显然y和x就是是正比例关系

线性与非线性的基本\u000B定义、主要区别\u000B及界定方法非线性的特点是：横断各个专业，渗透各个领域，几乎可以说是：“无处不在时时有。”确实如此。https://mp.weixin.qq.com/s?__biz=MzA4Nzg4MDY1Mw==&mid=2652410152&idx=4&sn=16d7fa55ec90d1c04a6b13a757e8df76&chksm=8bde978abca91e9c359534c9ceacab381fa162835c140ad91b7ced6f16d28f5ca3d93828f8e3&scene=27

2.2 一次函数的只是一种 直线性关系

• 一次函数，只是一种直线型关系
• 过原点的一次函数才是线性关系，y=ax是线性关系

2.3 线性的严格定义

• 线性：linear
• 非线性：non-linear，nonlinearity

线性，必须满足齐次性和可加性，才算线性

1. 齐次性：L(ax)=aL(x)
2. 可加性/叠加性/叠加原理：L(x+y)=L(x) + L(y)

从定义上看，因为 ky=k(ax+b)=kax+kb ≠  kax+b 所以  y=ax+b 确实不是线性关系！

线性代数中的矩阵 AX=Y，虽然是有矩阵做参数，但本质也是函数 ，都可以用线性函数的定义来看

2.4 向量和矩阵的平直概念（也是线性关系的另一种说法：图形上是直线，不能是2次函数，或指数函数等等）

矩阵的平直概念也属于线性无关的一种说法

有的地方有矩阵平直的概念，

• 即矩阵需要时线性增长的意思

1. 比如1个向量10，10个向量如果是100，那就是平直概念，其实就是按比例放大，直线比例，正相关比例，线性变换的意思。用图形上说，一般就是一根直线。
2. 其实完全可以说是，直线关系，倍数关系，正比例关系等等
3. 比如1个向量10，10个向量如果是90，那就不是平直概念，其实就是没按比例放大，比如是是一种其他类型的函数，比如二次函数，三次函数

3   从函数的角度看线性

一般的相法就是，函数里的线性，应该就是直线性吧？这样对吗？

3.1 一些函数的定义回顾

• 一元函数, 只有1个自变量的函数，y=F(x)
• 二元函数, 只有2个自变量的函数，z=F(x,y)
• ...

• 一次函数,  形如 y=F(x)= ax+.....+b 之类的函数，所有自变量的次数最高为1
• 甚至 y=sinx也是一次函数
• 二次函数,  形如 y=F(x)= ax^2+bx.....+c 之类的函数，所有自变量的最高次为2次
• ...

• 一元一次函数,  形如 y=F(x)= ax+.....+b 之类的函数
• 二元一次函数,  形如 z=F(x,y)= ax+by.....+c 之类的函数
• 二元二次函数,  形如 z=F(x,y)= ax^2+bx+cy^2.....+c 之类的函数

3.2 函数与几何图形的对应

• 一次函数，y=ax+b 在2维空间是一条直线
• 一次函数，z=ax+by+c 在3维空间是一个平面
• 2元1次函数  z=F(x,y)=ax+by+c 可以形变为 ax+by-z+c=0 就是3维空间里的一个平面

• 2次函数，y=ax^2 在2维空间是一条曲线
• 2次函数，y=ax^2+by^2+c 在3维空间是一个曲面

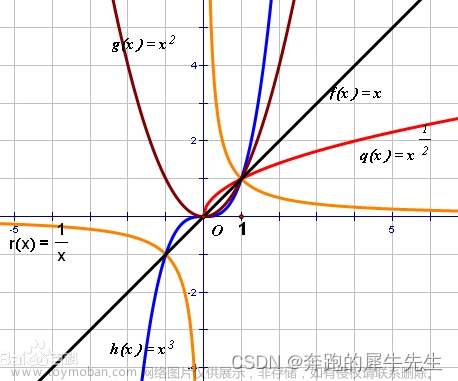
3.3 一次函数和线性函数 不是一回事

3.3.1 一次函数：形如如 y=ax+b  或  z=ax+by+c

• 只能叫 直线性关系
• 函数和自变量之间存在一次方函数关系
• 图形是上是一条直线，如 y=ax+b有斜率a 和截距b
• 极端的例子，y=cosx 是一次函数，但是不是线性函数

3.3.2 特殊一次函数：形如y=ax 或 z=ax+by

• 图形上是过原点的一次函数，如 y=ax 只有斜率
• 这个叫线性关系，或者 正比例关系/正相关关系

3.4 函数和矩阵的联系

3.4.1 函数和矩阵

• y=ax，是函数
• y=Ax，是函数，也是矩阵变换，其中A是矩阵，y,x 都是向量
• 本质 y=ax  和 y=Ax 就是一回事

3.4.2 函数方程组 和 矩阵

• 矩阵就是由向量组成的
• 向量/数组
• 函数方程组 → 系数矩阵 → 增广矩阵
• 所以函数的线性相关，在矩阵里也很重要

3.5 某种意义上说，这就是线性代数的本质？

• y=ax，是函数，y和x是单个数字
• y=Ax，是函数，也是矩阵变换，其中A是矩阵，y,x 都是向量
• 但是本质 y=ax  和 y=Ax 就是一回事可以统一起来
• 所以，线性代数，其实就是处理 向量/数组的数学，而不是处理单个数字的数学！？

4 线性相关在向量/矩阵里的作用和应用

4.1 线性相关

线性相关是针对个多个变量说的

• 2个向量，它们线性相关，或线性无关
• 3个向量，它们线性相关，或线性无关
• ....
• n个向量，它们线性相关，或线性无关

4.2 线性相关的严格定义

• 正面：线性相关---→ 就是等价向量
• 反面：线性无关/线性独立

4.2.1 直观的感觉

• 某向量经过线性变化后可以变换成另外一个向量，
• 如果有多个向量，其中一个可以被其他向量线性组成，那么就是线性相关的，否则就是线性无关的
• 比如 {1,2,3} ,{2,4,6} 这2个向量显然就是线性相关的
• 也就是{2,4,6} =2*{1,2,3} = {2*1,2*2,2*3}

4.2.2 原始严格定义1（更直观：1个向量与多个其他向量的关系）

注意这里，α1是一个数组/向量，而不是数组里的一个具体的数字,比如α1={x1,x2......}

(线性代数矩阵等肯定是研究 数组/向量之间的关系，而绝不是单个数字之间的关系)

如果 A中的多个向量： α1, α2, α3, .....αn ，如果存在一组实数k1,k2,k3....kn，

可以使得b=k1*α1+ k2*α2+...+ kn*αn ,

那么b 就和A包含这多个向量组 α1, α2, α3.....αn是线性相关的。

这一组实数k1,k2,k3....kn不要求全不为0

举例子

• RGB，比如 (255,255,0)  可以用 k1* (100,100,0) +k2* (0,255,0) 组成，所有是线性相关的，所以(255,255,0) 和k1* (100,100,0) +k2* (0,255,0) 某些时候是等价的。
•  (255,255,0) =255/100* (100,100,0) +0* (0,255,0) 其实  (255,255,0)与(100,100,0) 这1个向量就已经线性相关 了
• RGB，比如 (255,0,0)不能用 k1*  (0,100,100)+  k2* (0,255,0) 组成，怎么都不行，所以是线性无关的。

4.2.3 严格定义2 （把 所有要比较的向量看作一个整体）

注意这里，α1是一个数组/向量，而不是数组里的一个具体的数字,比如α1={x1,x2......} 

(线性代数矩阵等肯定是研究 数组/向量之间的关系，而绝不是单个数字之间的关系)

如果 A中的多个向量：α1, α2, α3, .....αn ，如果存在不全部为0的一组实数k1,k2,k3....kn，可以使得k1*α1+ k2*α2+...+ kn*αn=0 ,

那么这些向量 α1, α2, α3, α4, .....αn就是线性相关的

4.2.4  线性相关的几何意义

线性相关是针对个多个变量说的，那这些变量如果线性相关会有什么几何表现呢？

• 2个向量
• 3个向量
• ....
• n个向量

1维向量之间线性相关？有意义吗？

• 首先一维向量，都是数轴直线上的一个点，看不出什么几何意义

2维向量之间线性相关

• 2个2维向量线性相关

1. 在XOY平面上的同一条直线上，方向相同或不同
2. 在XOY平面是平行关系（理论上存在，实际上xoy向量空间里没这种向量）----我觉得向量的空间里，所有向量都是从原点出发的，因此，不存在有2个向量平行这种说法和可能性。所以才可以用终点坐标(0,1) 这种就代表了一个向量，默认所有向量都是从原点出发的。

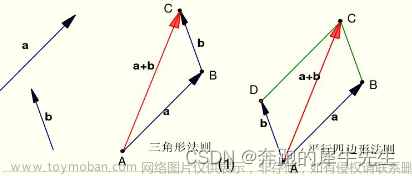
• 3个2维向量线性相关

1. 其中1个可以线性变化为另外1个
2. 其中2个可以线性变化为另外1个，就是这2个向量可以线性相加为第3个，就是三角形关系

• 4个2维向量线性相关

1. 其中1个可以线性变化为另外1个
2. 其中2个可以线性变化为另外1个
3. 其中3个可以线性变化为另外1个，就是这3个向量可以线性相加为第4个

......

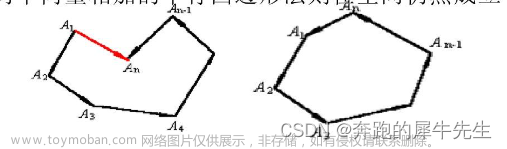
多个3维向量之间的线性相关的几何关系就不好想象了

4.3 线性组合的意思

• 比如某向量组{v1,v2...vn}  可以是2个，3个或更多
• 但是一般是2个向量组--组成XOY平面，而3个向量组组成XOYOZ空间
• V=span(v1,v2,....,vn) ={k1v1+k2v2+....+kb*vn}
• 也就是某向量组{v1,v2...vn} 进行任意线性组合，其结果仍然在向量空间内。

4.3.1 线性组合的具体方法

线性组合的方法包含如下这些：

• 加法
• 标量乘法

4.4 线性变换(可以线性变换的矩阵之间是等价矩阵)

如果1个矩阵可以线性变换位另外一个矩阵，那么这两个矩阵就是等价矩阵

4.4.1 线性变换内容

• 矩阵的初等行变换与初等列变换合称为矩阵的初等变换。
• 矩阵的初等行变换

1. 交换矩阵的两行
2. 以一个非零数k (倍数) 乘矩阵的某一行所有元素
3. 把矩阵的某一行所有元素乘以一个数k后加到另一行对应的元素 (倍加)

• 矩阵的初等列变换

1. 交换矩阵的两列
2. 以一个非零数k (倍数)乘矩阵的某一列所有元素
3. 把矩阵的某一列所有元素乘以一个数k后加到另一列对应的元素 (倍加)

4.4.2 线性变换的作用举例（作用很多，很大）

• 如果1个矩阵可以线性变换位另外一个矩阵，那么这两个矩阵就是等价矩阵
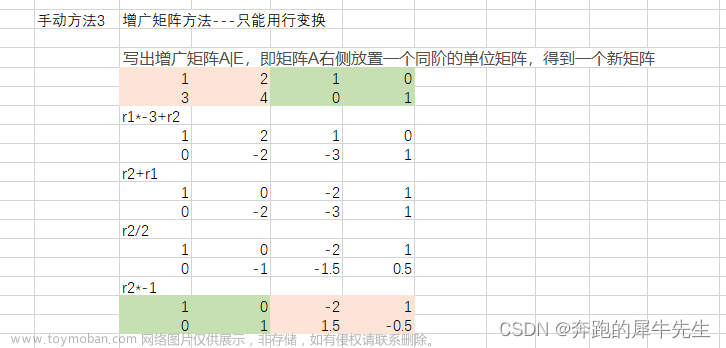
• 可以利用线性变换求矩阵的逆矩阵，见下面增广矩阵方法
• 线性变化，变成最简矩阵，求矩阵的秩
• 线性变化，变成上三角矩阵等等
• 线性变化，变成对角矩阵等等

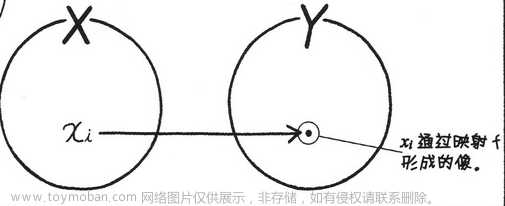
4.5 线性变换（线性映射）的意义？

线性变换，指的是线性空间上，满足

T(α+β)=T(α)+T(β)

T(kα)=kT(α)

那这和直线有什么关系？

• 见线性相关的定义，这个和成正反比例关系很大，和直线的关系也有！
• 标量乘法：数乘运算，可以看作直线上做伸缩+方向变换
• 加法运算：可以用三角形法则，首位相接的形式可以来解释，2个分段向量可以等价于1个总向量图形上生成的还是直线。
• 这种映射把空间里原来的 直线，仍然映射成 直线，而不会“扭曲”成曲线；
• 同时保持原点不动(原点动的就叫“仿射变换”了…)

4.6 线性相关的其他意义

• 如果不用空间的视角，
• 比如用RGB颜色叠加的思路，加入有一种维度更高的色彩构成比如RGBXXX
• 其实3维，4维。。。n维不过都是多个向量空间叠加而成

5 线性无关/线性独立

5.1  线性无关的定义

• 与前面的定义相反

5.2 线性无关有什么用呢？

线性无关最典型的例子：文章来源地址https://www.toymoban.com/news/detail-620288.html

• 向量空间的基之间都是线性无关的。（线性相关的向量无法作为线性空间的基）

6 线性代数的本质

6.1 线性代数和普通代数的区别

• 有种说法是这样的

1. 普通代数，就是以 单个数为研究对象的数学
2. 线性代数，就是以 数组（数组/向量：把多个数当作整体）为研究对象的数学

6.2 某种意义上说，这就是线性代数的本质？

• y=ax，是函数，y和x是单个数字
• y=Ax，是函数，也是矩阵变换，其中A是矩阵，y,x 都是向量/矩阵
• 但是本质 y=ax  和 y=Ax 就是一回事可以统一起来
• 所以，线性代数，其实就是处理 向量/数组的数学，而不是处理单个数字的数学！？

6.3 对应到EXCEL的操作，EXCEL的数组公式= 线性代数计算

• 工作表函数，公式的操作对象是1个单元格
• 数组函数，公式的操作对象是数组（多个单元格）
• 这么理解数组公式，其实是挺高级的

6.4 线性代数的核心是什么

• 核心是线性空间(向量空间)，及其线性映射
• 矩阵其实是线性变换的一个额外生造出来的辅助工具，1个类似 y=ax的参数数字a的类似的1个多维参数

6.5 线性代数是人造的，还是自然的？

• 从我的层面，我只能理解到，这是数学家们发明的一个精巧的工具，用来认识世界和解决问题的数学工具，思考工具，计算工具
• 笛卡尔的坐标系是一种线性坐标系（一般是指 直角坐标系）
• 而线性代数，在努力摆脱坐标系的影响，其实坐标系在线性代数里就是基，而比如向量矩阵，除了默认的自然基 (0,1) (1,0) 这种，理论上可以有无数组非线性相关的基，也就是坐标系可以很灵活选择，也可以很灵活的变换，不需要非是某些特别的坐标系。

到了这里，关于线性代数的学习和整理2：线性代数的基础知识(整理ing)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！