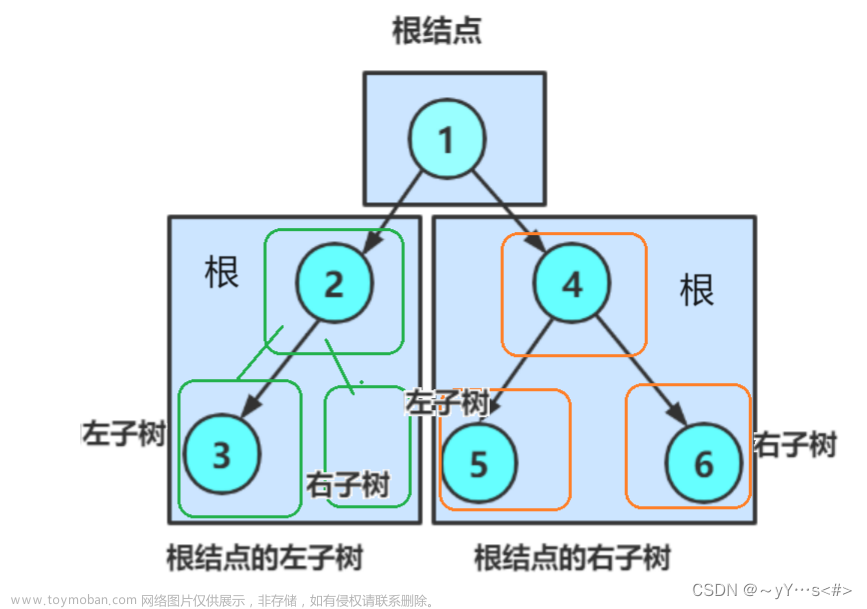
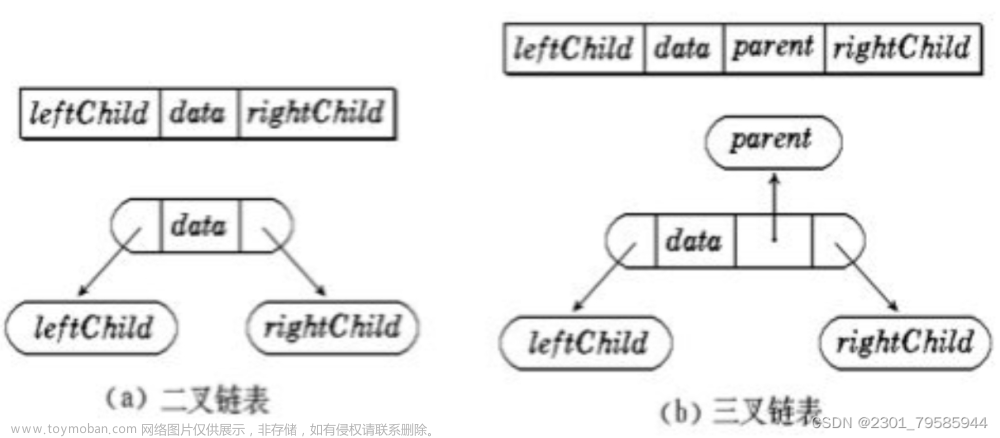
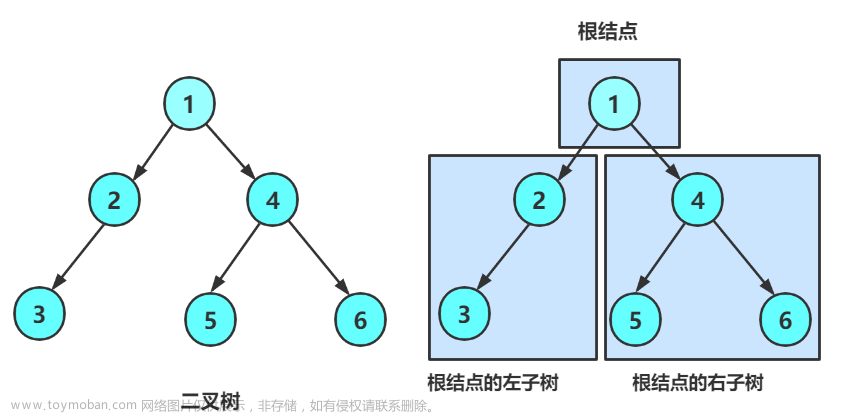
二叉树的链式存储-Toy模板网

这篇具有很好参考价值的文章主要介绍了二叉树的链式存储。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

二叉树的链式存储

//
//  main.c
//  LinkBiTree
//
//  Created by Eason on 2020/8/10.
//  Copyright © 2020 Eason. All rights reserved.
//

#include <string.h>
#include <stdlib.h>
#include "math.h"
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
#define MAXSIZE 100   //二叉树的最大长度
typedef char ElemType;  //二叉树的数据元素类型
typedef int Status;   //用int作为状态类型，对应预定义的OK ERROR TRUE FALSE
int i=1;   //创建二叉树时的字符串定位器
typedef char String[MAXSIZE];   //定义一个字符数组作为字符串来创建二叉树
String S;   //数组对象
typedef struct BTNode   //二叉树的链式存储结构
{
   ElemType data;
   struct BTNode *leftChild,*rightChild;
}BTNode,*BTree;   //BTree = *BTNode

//字符串初始化（将ch长度地址范围里的字符依次读入字符串中）
Status initString(String S, char *ch){
    if(strlen(ch)>=MAXSIZE){   //判断用来初始化的字符长度是否超出预定义的字符串长度
        return ERROR;
    }
    S[0] = strlen(ch);   //S[0]用来存储字符串长度
    int loc=0;   //ch定位器
    for(int i=1;i<=S[0];i++){   //依次循环读入字符串中
        S[i] = *(ch+loc);   //当前ch下一个地址的ch
        loc++;   //加到第几个位置的ch
    }
    printf("字符串初始化完成\n");
    return OK;
}

//打印字符串
Status printString(String S){   //没啥好说的就是个循环遍历打印初始化过的字符串
    for(int i=0;i<=strlen(S);i++){
        printf("%c ", S[i]);
    }
    printf("\n");
    return OK;
}
//初始化链二叉树
Status initTree(BTree *T){   //将二叉树的根结点置为空则初始化成功
    *T=NULL;
    printf("初始化成功！\n");
    return OK;
}

//判断链二叉树是否为空
Status isEmpty(BTree T){  //若二叉树的根结点为空，则此树为空
    if(T==NULL){
        return TRUE;
    }else{
        return FALSE;
    }
}

//创建链二叉树（利用初始化的字符串向二叉树中读入来创建二叉树）
void createBTree(BTree *T){
    ElemType ch;   //临时字符存储器
    ch = S[i++];   //将当前数组的位置的字符读入ch中后位置++
    if(ch=='#'){   //若字符为‘#’则说明此位置为空
        *T=NULL;   //则将此位置置为空
    }else{
        *T=(BTree)malloc(sizeof(BTNode));  //若此处的字符不为空，则为其分配一个结点大小的内存
        if(!*T){   //判断能否为新结点申请内存
            printf("内存分配失败\n");
            exit(OVERFLOW);
        }else{   //分配内存成功
            (*T)->data = ch;   //将此位置的数据置为对应的字符值
            createBTree(&(*T)->leftChild);   //递归继续寻找是否左孩子结点存在若存在则按照步骤分配内存成立对应的结点，若无则返回向下
            createBTree(&(*T)->rightChild);   //此时是若结点无左孩子则递归寻找是否是有右孩子若有则按照步骤分配内存成立对应的结点，若无则返回上一级的结点判断右孩子继续递归
        }
    }
}

//销毁二叉树（清空二叉树clearBTree()相同）
Status destroyBTree(BTree *T){
    if(*T){   //若当前结点存在
        if((*T)->leftChild){   //则判断是否有左孩子，若有则先销毁左孩子
            destroyBTree(&(*T)->leftChild);   //递归销毁左孩子
        }
        if((*T)->rightChild){   //无左孩子则判断是否有右孩子，若有则销毁右孩子
            destroyBTree(&(*T)->rightChild);   //递归销毁右孩子
        }
        free(*T);   //若都没有则释放当前结点
        *T=NULL;   //将结点置空
    }
    return OK;
}

//获得二叉树的深度
int getDepth(BTree *T){
    int deep = 0;   //深度计数
    if(*T!=NULL){   //如果当前结点不为空
        int leftdeep = getDepth(&(*T)->leftChild);   //则先判断其左子树的深度
        int rightdeep = getDepth(&(*T)->rightChild);  //然后判断右子树的深度
        deep = leftdeep>=rightdeep?leftdeep+1:rightdeep+1;   //二叉树的深度对应左右子树中最大的一个 再加上当前的深度1
    }
    return deep;   //将深度值返回
}

//获取根结点的数据
char getRoot(BTree T){
    if(isEmpty(T)){   //判断二叉树是否为空
        printf("根结点不存在，无法获取\n");
        return ERROR;
    }
    return T->data;   //若二叉树不为空，则返回当前结点的数据域
}

//获取指定结点的数据
char getValue(BTree T){
    if(isEmpty(T)){   //判断当前结点是否存在
        printf("当前结点不存在，无法获取\n");
        return ERROR;
    }
    return T->data;   //返回当前结点的数据
}

//为指定结点的数据更换数值（将结点T的数据域更换为指定的value值）
Status replaceValue(BTree *T, char *value){
    (*T)->data = *value;   //将制定的value值替换入指定结点的数据域中
    return OK;
}

//前序遍历
void preOrederTraverse(BTree T){
    if(T==NULL){    //判断当前结点是否存在，不存在则推出当前方法返回上一级，若无上一级则退出
        return;
    }
    printf("%c ", T->data);   //先访问根结点
    preOrederTraverse(T->leftChild);   //后遍历左子树
    preOrederTraverse(T->rightChild);   //最后遍历右子树
}

//中序遍历
void inOrderTraverse(BTree T){
    if(T==NULL){   //判断当前结点是否存在，不存在则推出当前方法返回上一级，若无上一级则退出
        return;
    }
    inOrderTraverse(T->leftChild);   //先遍历左子树
    printf("%c ", T->data);   //后访问根结点
    inOrderTraverse(T->rightChild);   //最后遍历右子树
}

//后序遍历
void postOrderTraverse(BTree T){
    if(T==NULL){   //判断当前结点是否存在，不存在则推出当前方法返回上一级，若无上一级则退出
        return;
    }
    postOrderTraverse(T->leftChild);    //先遍历左子树
    postOrderTraverse(T->rightChild);   //再遍历右子树
    printf("%c ", T->data);   //最后访问根结点
}


//测试
int main()
{
    BTree T;
    initTree(&T);
    initString(S, "EASO#N###H##EGO###G#O##");
    printf("字符串初始为：\n");
    printString(S);
    printf("创建二叉树T\n");
    createBTree(&T);
    printf("完成创建二叉树T\n");
    printf("二叉树的深度为:%d\n", getDepth(&T));
    printf("前序遍历二叉树T:\n");
    preOrederTraverse(T);
    printf("\n中序遍历二叉树T:\n");
    inOrderTraverse(T);
    printf("\n后序遍历二叉树T:\n");
    postOrderTraverse(T);
    printf("\n此时的根结点为：%c\n", getRoot(T));
    printf("将二叉树销毁后遍历可得：\n");
    destroyBTree(&T);
    preOrederTraverse(T);
    printf("此时的根结点为：%c\n", getRoot(T));
    return 0;
}

文章来源地址https://www.toymoban.com/news/detail-622513.html

到了这里，关于二叉树的链式存储的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！