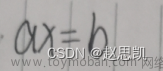【C++】开源：Eigen3矩阵与线性代数库配置使用-Toy模板网

这篇具有很好参考价值的文章主要介绍了【C++】开源：Eigen3矩阵与线性代数库配置使用。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

😏★,°:.☆(￣▽￣)/$:.°★ 😏
这篇文章主要介绍Eigen3线性代数模板库配置使用。
无专精则不能成，无涉猎则不能通。——梁启超
欢迎来到我的博客，一起学习，共同进步。
喜欢的朋友可以关注一下，下次更新不迷路🥞

😏1. 项目介绍

项目Gitlab地址：https://gitlab.com/libeigen/eigen

官网：https://eigen.tuxfamily.org/index.php?title=Main_Page

Eigen3 是一个开源的 C++ 模板库，用于线性代数和数值计算。它提供了高效、灵活和易于使用的矩阵、向量和线性代数运算功能，广泛应用于科学计算、机器学习、图像处理和工程领域等。重点是：轻量级，只包含头文件。

以下是 Eigen3 的一些主要特点和功能：

1.高性能：Eigen3 通过使用表达式模板技术，能够在编译时进行优化，并产生高度优化的机器码。这使得 Eigen3 在数值计算中具有出色的性能，并且比某些其他常见的线性代数库更快。

2.易于使用：Eigen3 提供了直观和简洁的 API，使得编写线性代数代码变得容易。它采用了类似于数学符号的语法，使得代码可读性强，更接近人类思维方式。

3.丰富的功能：Eigen3 提供了许多功能来支持常见的线性代数操作，包括矩阵和向量的基本运算（加、减、乘、除）、矩阵分解（LU、QR、SVD 等）、特征值和特征向量计算、线性方程组求解、矩阵代数操作（转置、逆、行列式等）以及各种线性代数算法。

4.平台无关性：Eigen3 是一个纯模板库，不依赖于任何特定的硬件或操作系统，因此可以在多个平台上使用和移植。

5.轻量级：Eigen3 的代码库非常小巧，只有头文件，易于集成到其他项目中。

6.兼容性：Eigen3 支持 C++11 或更高版本的编译器，并且与其他常见的 C++ 库和框架（如 STL、Boost 等）兼容。

😊2. 环境配置

下面进行环境配置：

# ubuntu安装
sudo apt install libeigen3-dev

要在项目中使用eigen3，可创建cmake工程，CMakeLists.txt示例：

cmake_minimum_required(VERSION 3.12)
project(useEigen)
set(CMAKE_CXX_STANDARD 11)

# 寻找Eigen库
find_package(Eigen3 REQUIRED)
# 将Eigen库include进来
include_directories(${EIGEN3_INCLUDE_DIRS})

add_executable(${PROJECT_NAME} main.cpp)

另外，简单的，可以在g++时带上头文件目录编译，示例：

g++ -o main main.cpp -I /usr/include/eigen3/ #（不加也可）

😆3. 使用说明

下面进行使用分析：

矩阵运算示例：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    // 以Xd方式声明一个3x3的矩阵
    MatrixXd mat(3, 3);
    // 将矩阵(0,0)位置元素赋为1.5
    mat(0, 0) = 1.5;
    cout << "MatrixXd:\n " << mat << endl;

    // 以Matrix方式声明一个5x2的矩阵
    Matrix<double, 5, 2> m1;
    cout << "Matrix:\n " << m1 << endl;

    // 随机数矩阵
    MatrixXd m2 = MatrixXd::Random(5, 3);
    cout << "MatrixXd::Random:\n " << m2 << endl;

    Eigen::MatrixXd matrix1(2, 2);
    matrix1 << 1, 2,
               3, 4;

    Eigen::MatrixXd matrix2(2, 2);
    matrix2 << 5, 6,
               7, 8;

	// 矩阵加法
    Eigen::MatrixXd result = matrix1 + matrix2;
    std::cout << "Matrix Addition:\n" << result << std::endl;

	// 矩阵乘法
    result = matrix1 * matrix2;
    std::cout << "Matrix Multiplication:\n" << result << std::endl;

    return 0;
}

向量运算示例：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    Vector3d v(1, 2, 3);
    cout << "ori vector:\n" << v << endl;
    cout << "* result:\n" << v * 3 << endl;
    // 点乘
    cout << "dot result:\n" << v.dot(v) << endl;
    // 叉乘
    cout << "cross result:\n" << v.cross(v) << endl;

    return 0;
}

求解线性方程组示例：

#include <iostream>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;

int main() {
    // 创建系数矩阵 A
    Matrix3d A;
    A << 2, 1, -1,
         -3, -1, 2,
         -2,  1, 2;

    // 创建右侧常数向量 b
    Vector3d b;
    b << 8, -11, -3;

    // 求解线性方程组 Ax=b
    Vector3d x = A.colPivHouseholderQr().solve(b);

    // 打印解向量 x
    std::cout << "Solution x = \n" << x << std::endl;

    return 0;
}