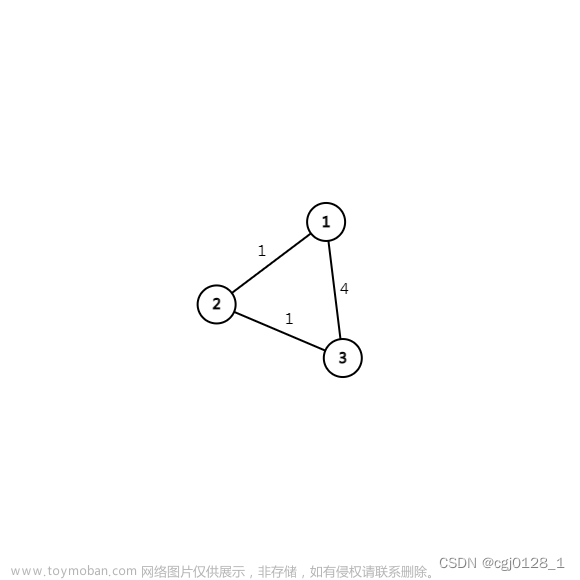
图论--最短路问题

图论–最短路问题

邻接表-链式前向星

/*
e[idx]:存储点的编号
w[idx]:存储边的距离（权重）
*/
void add(int a, int b, int c) {
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c
    h[a] = idx ++;
}

1.拓扑排序

给定一个 n 个点 m 条边的有向图，点的编号是 11 到 n，图中可能存在重边和自环。

请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出 −1−1。

若一个由图中所有点构成的序列 A 满足：对于图中的每条边 (x,y)，x在 A中都出现在 y 之前，则称 A是该图的一个拓扑序列。

输入格式

第一行包含两个整数 n 和 m。

接下来 m 行，每行包含两个整数 x 和 y，表示存在一条从点 x 到点 y的有向边 (x,y)。

输出格式

共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。

否则输出 −1−1。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>

using namespace std;

const int N = 1e5 + 10;

int n, m;

// 队列
int q[N], hh, tt = -1;

// 邻接表
int e[N], idx, ne[N], h[N];

// 入度
int d[N];

void add(int a, int b) {
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++;
}

bool topsort() {
    for (int i = 1; i <= n; i ++)
        if (!d[i])
            q[++ tt] = i;
    
    while (hh <= tt) {
        int tmp = q[hh ++];
        
        for (int i = h[tmp]; i != -1; i = ne[i]) {
            int j = e[i];
            d[j] --;
            if (!d[j])
                q[++ tt] = j;
        }
    }
    
    if (tt == n-1)  
        return true;
    return false;
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (m --) {
        int a, b;
        cin >> a >> b;
        add(a, b);
        d[b] ++;
    }
    if (topsort()) 
        for (int i = 0; i < n; i ++)
            cout << q[i] << ' ';
    else    
        cout << -1;
        
    return 0;
}

2.Dijkstra求最短路

稠密图（边很多）——邻接矩阵

所有边权都是正数,单源最短路

• 初始化到每个节点距离为无穷inf，初识节点距离dist[1] = 0

• 迭代n轮

• 每次从未标记的节点中选择距离出发点最近的节点，标记，收录到最优路径集合中

• 计算刚加入节点A的临近节点B的距离（不包含标记的节点）。若节点A的距离加节点A到B的距离小于节点B的距离，则更新节点B的距离。

给定一个 n 个点 m条边的有向图，图中可能存在重边和自环，所有边权均为正值。

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 −1。

输入格式

第一行包含整数 n 和 m。

接下来 m 行每行包含三个整数 x,y,z，表示存在一条从点 x到点 y 的有向边，边长为 z。

输出格式

输出一个整数，表示 1 号点到 n 号点的最短距离。

如果路径不存在，则输出 −1。

#include <iostream>
#include <algorithm>    
#include <cstring>
#include <cstdio>

using namespace std;

const int N = 505;

int n, m;

// 标记
int st[N];
// 距离
int dist[N];
// 邻接矩阵
int g[N][N];

int dijkstra() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    for (int i = 0; i < n; i ++) {
        int t = -1;
        // 选择距离出发点最近的节点
        for (int j = 1; j <= n; j ++) 
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
                t = j;
        st[t] = 1;
        for (int j = 1; j <= n; j ++) 
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    if (dist[n] == 0x3f3f3f3f)
        return -1;
    return dist[n];
}

int main() {
    memset(g, 0x3f, sizeof g);
    
    scanf("%d%d", &n, &m);
    
    for (int i = 1; i <= n; i ++)
        g[i][i] = 0;
        
    while (m --) {
        int x, y, z;
        scanf("%d%d%d", &x, &y, &z);
        g[x][y] = min(g[x][y], z);
    }
    
    int ans = dijkstra();
    printf("%d", ans);
    
    return 0;
}

堆优化

稀疏图（点很多）——邻接表

#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#include <cstdio>

using namespace std;

typedef pair<int, int> pii;

const int N = 1e6 + 10;

int n, m;

// 标记，避免自环
int st[N]; 

// 邻接表
int e[N], h[N], ne[N], w[N], idx;

void add(int a, int b, int c) {
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c;
    h[a] = idx ++;
}

int dist[N];

int dijkstra() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    // 小根堆 {边权(距离)，编号}
    priority_queue<pii, vector<pii>, greater<pii>> heap;
    heap.push({0, 1});
    while (!heap.empty()) {
        int v = heap.top().second, distance = heap.top().first;
        heap.pop();
        if (st[v])  
            continue;
        st[v] = 1;
        for (int i = h[v]; i != -1; i = ne[i]) 
            if (dist[e[i]] > dist[v] + w[i])
            {
                dist[e[i]] = dist[v] + w[i];
                heap.push({dist[e[i]], e[i]});
            }
    }


    if (dist[n] == 0x3f3f3f3f)  
        return -1;
    return dist[n];
}

int main() {
    memset(h, -1, sizeof h);
    scanf("%d%d", &n, &m);
    while (m --) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }
    int t = dijkstra();
    printf("%d", t);

    return 0;
}

3.Bellman-Ford算法（存在负权边，有边数限制最短路）

有负权回路，最短路不一定存在

for k 次

​ for 所有边 a, b, w

​ 松弛操作：dist[b] =min(dist[b,dist[a]+w)

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出从 1号点到 n 号点的最多经过 k 条边的最短距离，如果无法从 1 号点走到 n 号点，输出 impossible。

注意：图中可能 存在负权回路 。

#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

int dist[505], backup[505];
int n, m, k;

struct edge {
    int a, b, w;
} edges[10010];

void bellman_ford() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for (int i = 0; i < k; i ++) {
        memcpy(backup, dist, sizeof dist);
        for (int i = 0; i < m; i ++) {
            int a = edges[i].a, b = edges[i].b, w = edges[i].w;
            dist[b] = min(dist[b], w + backup[a]);
        }
    }
    
}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i < m; i ++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        edges[i] = {a, b, c};
    }
    bellman_ford();
    if (dist[n] > 0x3f3f3f3f / 2)   puts("impossible");
    else    printf("%d", dist[n]);

    return 0;
}

4.SPFA算法（与负权边，无负权回路）

给定一个 n个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出 1号点到 n 号点的最短距离，如果无法从 11 号点走到 n 号点，则输出 impossible。

数据保证不存在负权回路。

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

const int N = 1e5 + 10;

int idx, h[N], ne[N], e[N], w[N];

int n, m;

// 判断该点是否在队列
bool st[N];
int dist[N];

void add(int a, int b, int c) {
    e[idx] = b;
    ne[idx] = h[a];
    w[idx] = c;
    h[a] = idx ++;
}

int spfa() {
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    queue<int> q;
    q.emplace(1);
    st[1] = 1;
    while (!q.empty()) {
        int t = q.front();
        q.pop();
        st[t] = 0;
        for (int i = h[t]; i != -1; i = ne[i]) {
            if (dist[e[i]] > dist[t] + w[i]) {
                dist[e[i]] = dist[t] + w[i];
                if (!st[e[i]]) {
                    q.emplace(e[i]);
                    st[e[i]] = 1;
                }
            }
        }
    }
    return dist[n];
}

int main() {
    ios::sync_with_stdio(false);
    memset(h, -1, sizeof h);
    cin >> n >> m;
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    int t = spfa();
    if (t == 0x3f3f3f3f)    cout << "impossible" << endl;
    else    cout << t;

    return 0;

}

5.Floyd求在求最短路（多源）

给定一个 n 个点 m条边的有向图，图中可能存在重边和自环，边权可能为负数。

再给定 k 个询问，每个询问包含两个整数 x 和 y，表示查询从点 x 到点 y 的最短距离，如果路径不存在，则输出 impossible。

数据保证图中不存在负权回路。文章来源地址https://www.toymoban.com/news/detail-623806.html

#include <iostream> 
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 210, inf = 1e9;

int d[N][N];

int n;

void floyd() {
    for (int k = 1; k <= n; ++k) {
        for (int i = 1; i <= n; ++i)
            for (int j = 1; j <= n; ++j) 
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
    }
}

int main() {
    int m, k;
    cin >> n >> m >> k;
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= n; ++j) {
            if (i == j)     d[i][j] = 0;
            else    d[i][j] = inf;
        }
    while (m--) {
        int a, b, c;
        cin >> a >> b >> c;
        d[a][b] = min(d[a][b], c);
    }
    floyd();
    while (k--) {
        int a, b;
        cin >> a >> b;
        if (d[a][b] > inf / 2)      puts("impossible");
        else    cout << d[a][b]<<endl;
    }

    return 0;
}

到了这里，关于图论--最短路问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！