1、问题描述
一套 1000 平方英尺 (sqft) 的房屋售价为300,000美元,一套 2000 平方英尺的房屋售价为500,000美元。这两点将构成我们的数据或训练集。面积单位为 1000 平方英尺,价格单位为 1000 美元。
| Size (1000 sqft) | Price (1000s of dollars) |
|---|---|
| 1.0 | 300 |
| 2.0 | 500 |
希望通过这两个点拟合线性回归模型,以便可以预测其他房屋的价格。例如,面积为 1200 平方英尺的房屋价格是多少。
首先导入所需要的库
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
以下代码来创建x_train和y_train变量。数据存储在一维 NumPy 数组中。
# x_train is the input variable (size in 1000 square feet)
# y_train is the target (price in 1000s of dollars)
x_train = np.array([1.0, 2.0])
y_train = np.array([300.0, 500.0])
print(f"x_train = {x_train}")
print(f"y_train = {y_train}")
2、表示说明
使用 m 来表示训练样本的数量。 (x ( i ) ^{(i)} (i), y ( i ) ^{(i)} (i)) 表示第 i 个训练样本。由于 Python 是零索引的,(x ( 0 ) ^{(0)} (0), y ( 0 ) ^{(0)} (0)) 是 (1.0, 300.0) , (x ( 1 ) ^{(1)} (1), y ( 1 ) ^{(1)} (1)) 是 (2.0, 500.0).
3、数据绘图
使用 matplotlib 库中的scatter()函数绘制这两个点。 其中,函数参数marker 和 c 将点显示为红叉(默认为蓝点)。使用matplotlib库中的其他函数来设置要显示的标题和标签。
# Plot the data points
plt.scatter(x_train, y_train, marker='x', c='r')
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.show()

4、模型函数
线性回归的模型函数(这是一个从 x 映射到 y 的函数)可以表示为
f
w
,
b
(
x
(
i
)
)
=
w
x
(
i
)
+
b
(1)
f_{w,b}(x^{(i)}) = wx^{(i)} + b \tag{1}
fw,b(x(i))=wx(i)+b(1)
计算 f w , b ( x ( i ) ) f_{w,b}(x^{(i)}) fw,b(x(i)) 的值,可以将每个数据点显示地写为:
对于
x
(
0
)
x^{(0)}
x(0), f_wb = w * x[0] + b
对于
x
(
1
)
x^{(1)}
x(1), f_wb = w * x[1] + b
对于大量的数据点,这可能会变得笨拙且重复。 因此,可以在for 循环中计算输出,如下面的函数compute_model_output 所示。
def compute_model_output(x, w, b):
"""
Computes the prediction of a linear model
Args:
x (ndarray (m,)): Data, m examples
w,b (scalar) : model parameters
Returns
y (ndarray (m,)): target values
"""
m = x.shape[0]
f_wb = np.zeros(m)
for i in range(m):
f_wb[i] = w * x[i] + b
return f_wb
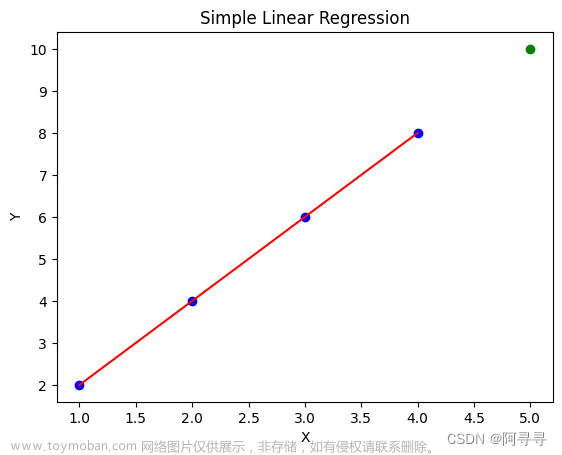
调用 compute_model_output 函数并绘制输出
w = 100
b = 100
tmp_f_wb = compute_model_output(x_train, w, b,)
# Plot our model prediction
plt.plot(x_train, tmp_f_wb, c='b',label='Our Prediction')
# Plot the data points
plt.scatter(x_train, y_train, marker='x', c='r',label='Actual Values')
# Set the title
plt.title("Housing Prices")
# Set the y-axis label
plt.ylabel('Price (in 1000s of dollars)')
# Set the x-axis label
plt.xlabel('Size (1000 sqft)')
plt.legend()
plt.show()

很明显,
w
=
100
w = 100
w=100 和
b
=
100
b = 100
b=100 不会产生适合数据的直线。
根据学过的数学知识,可以容易求出 w = 200 w = 200 w=200 和 b = 100 b = 100 b=100
5、预测
现在我们已经有了一个模型,可以用它来做出房屋价格的预测。来预测一下 1200 平方英尺的房子的价格。由于面积单位为 1000 平方英尺,所以 x x x 是1.2。
w = 200
b = 100
x_i = 1.2
cost_1200sqft = w * x_i + b
print(f"${cost_1200sqft:.0f} thousand dollars")
输出的结果是:$340 thousand dollars文章来源:https://www.toymoban.com/news/detail-624117.html
总结
- 线性回归建立一个特征和目标之间关系的模型
- 在上面的例子中,特征是房屋面积,目标是房价。
- 对于简单线性回归,模型有两个参数 w w w 和 b b b ,其值使用训练数据进行拟合。
- 一旦确定了模型的参数,该模型就可以用于对新数据进行预测。
附录
deeplearning.mplstyle 源码:文章来源地址https://www.toymoban.com/news/detail-624117.html
# see https://matplotlib.org/stable/tutorials/introductory/customizing.html
lines.linewidth: 4
lines.solid_capstyle: butt
legend.fancybox: true
# Verdana" for non-math text,
# Cambria Math
#Blue (Crayon-Aqua) 0096FF
#Dark Red C00000
#Orange (Apple Orange) FF9300
#Black 000000
#Magenta FF40FF
#Purple 7030A0
axes.prop_cycle: cycler('color', ['0096FF', 'FF9300', 'FF40FF', '7030A0', 'C00000'])
#axes.facecolor: f0f0f0 # grey
axes.facecolor: ffffff # white
axes.labelsize: large
axes.axisbelow: true
axes.grid: False
axes.edgecolor: f0f0f0
axes.linewidth: 3.0
axes.titlesize: x-large
patch.edgecolor: f0f0f0
patch.linewidth: 0.5
svg.fonttype: path
grid.linestyle: -
grid.linewidth: 1.0
grid.color: cbcbcb
xtick.major.size: 0
xtick.minor.size: 0
ytick.major.size: 0
ytick.minor.size: 0
savefig.edgecolor: f0f0f0
savefig.facecolor: f0f0f0
#figure.subplot.left: 0.08
#figure.subplot.right: 0.95
#figure.subplot.bottom: 0.07
#figure.facecolor: f0f0f0 # grey
figure.facecolor: ffffff # white
## ***************************************************************************
## * FONT *
## ***************************************************************************
## The font properties used by `text.Text`.
## See https://matplotlib.org/api/font_manager_api.html for more information
## on font properties. The 6 font properties used for font matching are
## given below with their default values.
##
## The font.family property can take either a concrete font name (not supported
## when rendering text with usetex), or one of the following five generic
## values:
## - 'serif' (e.g., Times),
## - 'sans-serif' (e.g., Helvetica),
## - 'cursive' (e.g., Zapf-Chancery),
## - 'fantasy' (e.g., Western), and
## - 'monospace' (e.g., Courier).
## Each of these values has a corresponding default list of font names
## (font.serif, etc.); the first available font in the list is used. Note that
## for font.serif, font.sans-serif, and font.monospace, the first element of
## the list (a DejaVu font) will always be used because DejaVu is shipped with
## Matplotlib and is thus guaranteed to be available; the other entries are
## left as examples of other possible values.
##
## The font.style property has three values: normal (or roman), italic
## or oblique. The oblique style will be used for italic, if it is not
## present.
##
## The font.variant property has two values: normal or small-caps. For
## TrueType fonts, which are scalable fonts, small-caps is equivalent
## to using a font size of 'smaller', or about 83%% of the current font
## size.
##
## The font.weight property has effectively 13 values: normal, bold,
## bolder, lighter, 100, 200, 300, ..., 900. Normal is the same as
## 400, and bold is 700. bolder and lighter are relative values with
## respect to the current weight.
##
## The font.stretch property has 11 values: ultra-condensed,
## extra-condensed, condensed, semi-condensed, normal, semi-expanded,
## expanded, extra-expanded, ultra-expanded, wider, and narrower. This
## property is not currently implemented.
##
## The font.size property is the default font size for text, given in points.
## 10 pt is the standard value.
##
## Note that font.size controls default text sizes. To configure
## special text sizes tick labels, axes, labels, title, etc., see the rc
## settings for axes and ticks. Special text sizes can be defined
## relative to font.size, using the following values: xx-small, x-small,
## small, medium, large, x-large, xx-large, larger, or smaller
font.family: sans-serif
font.style: normal
font.variant: normal
font.weight: normal
font.stretch: normal
font.size: 8.0
font.serif: DejaVu Serif, Bitstream Vera Serif, Computer Modern Roman, New Century Schoolbook, Century Schoolbook L, Utopia, ITC Bookman, Bookman, Nimbus Roman No9 L, Times New Roman, Times, Palatino, Charter, serif
font.sans-serif: Verdana, DejaVu Sans, Bitstream Vera Sans, Computer Modern Sans Serif, Lucida Grande, Geneva, Lucid, Arial, Helvetica, Avant Garde, sans-serif
font.cursive: Apple Chancery, Textile, Zapf Chancery, Sand, Script MT, Felipa, Comic Neue, Comic Sans MS, cursive
font.fantasy: Chicago, Charcoal, Impact, Western, Humor Sans, xkcd, fantasy
font.monospace: DejaVu Sans Mono, Bitstream Vera Sans Mono, Computer Modern Typewriter, Andale Mono, Nimbus Mono L, Courier New, Courier, Fixed, Terminal, monospace
## ***************************************************************************
## * TEXT *
## ***************************************************************************
## The text properties used by `text.Text`.
## See https://matplotlib.org/api/artist_api.html#module-matplotlib.text
## for more information on text properties
#text.color: black
到了这里,关于【机器学习】Linear Regression的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!

![[github-100天机器学习]day3 multiple linear regression--代码版本问题已修正](https://imgs.yssmx.com/Uploads/2024/02/525371-1.png)