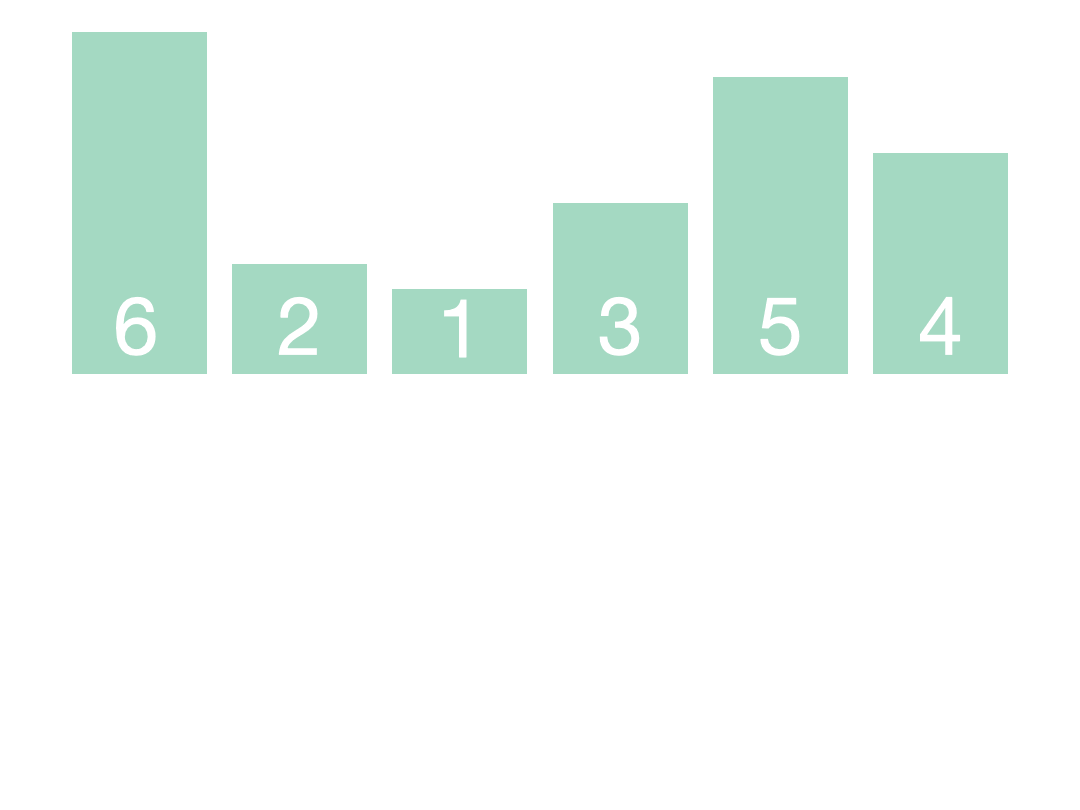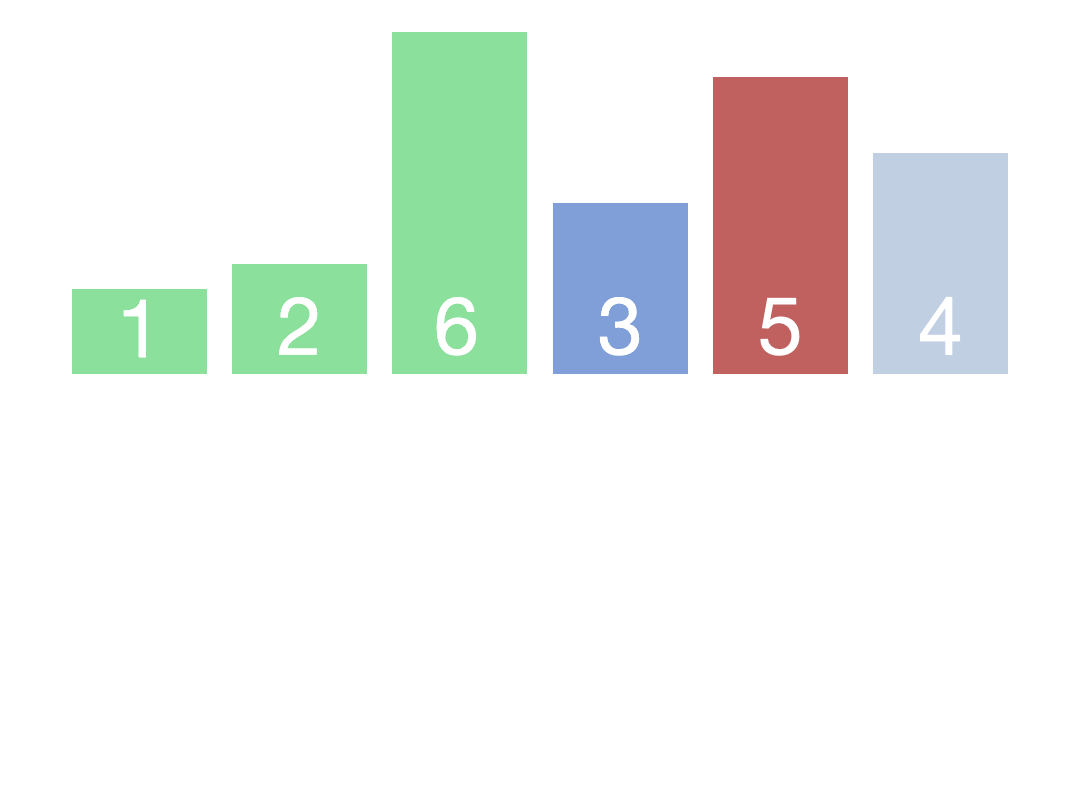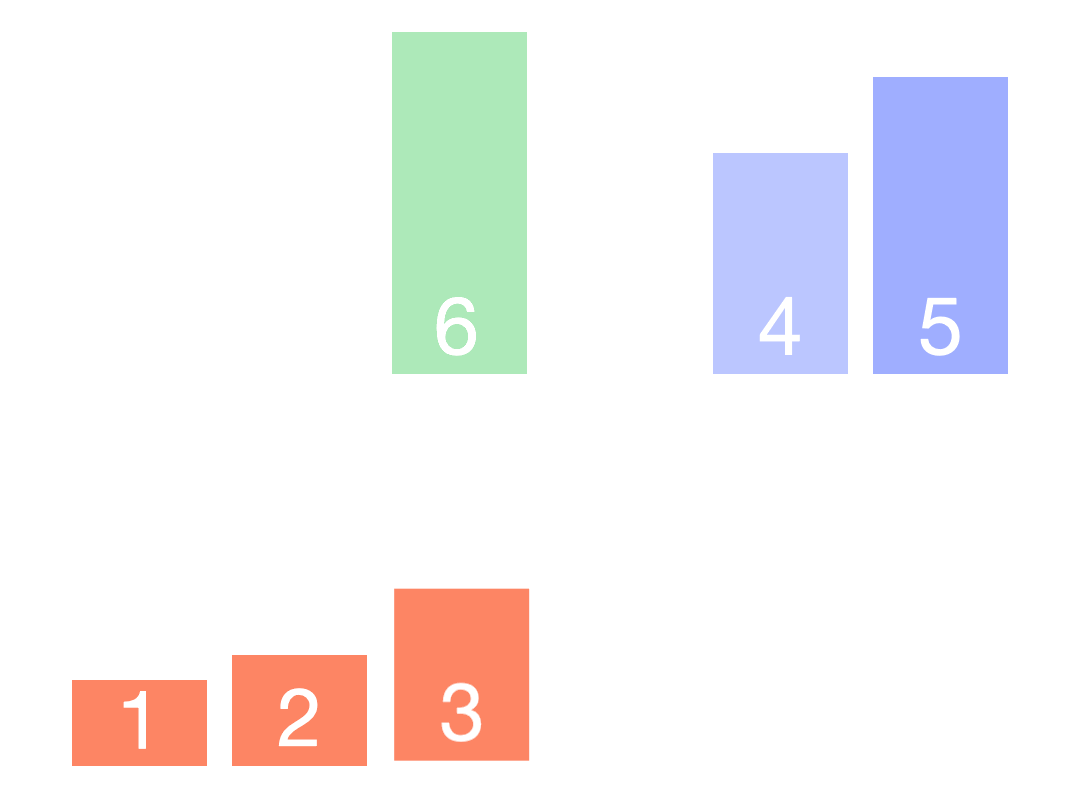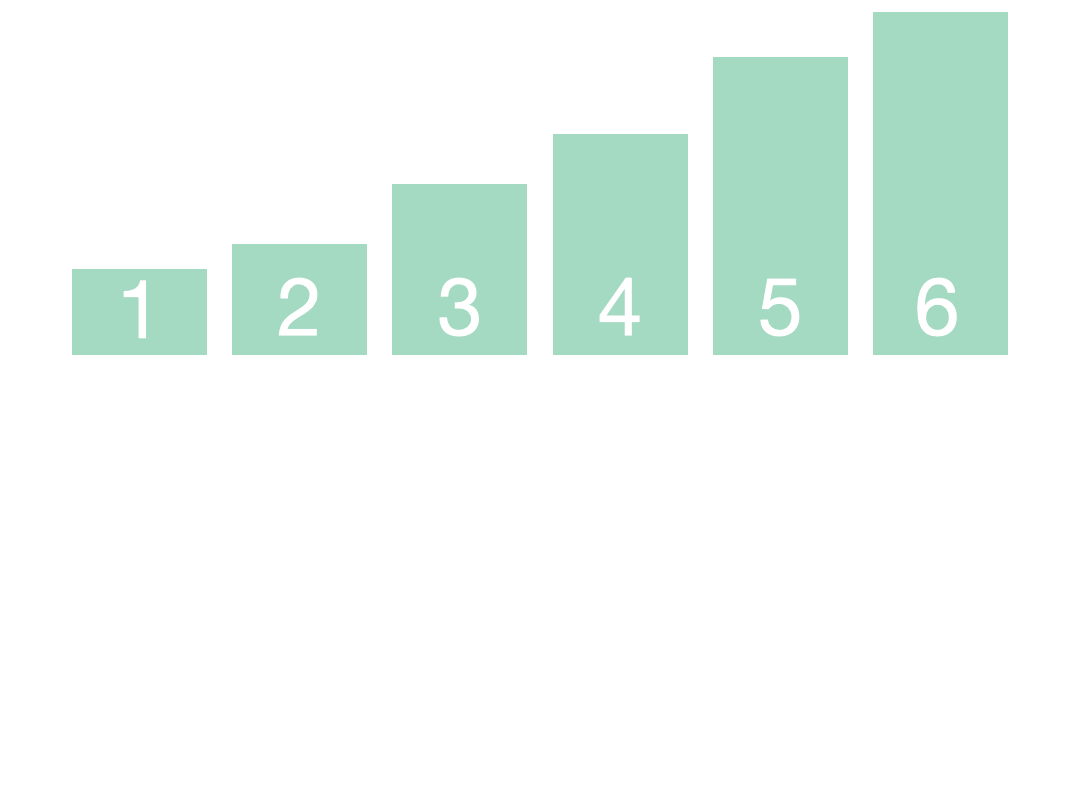小程一言
这篇文章是在排序进行曲3.0之后的续讲，
这篇文章主要是对快速排序进行细致分析，以及操作。
希望大家多多支持
快速排序
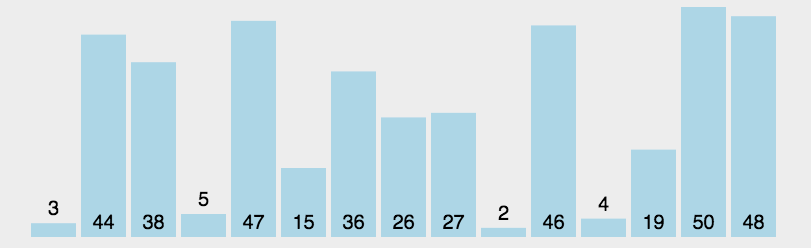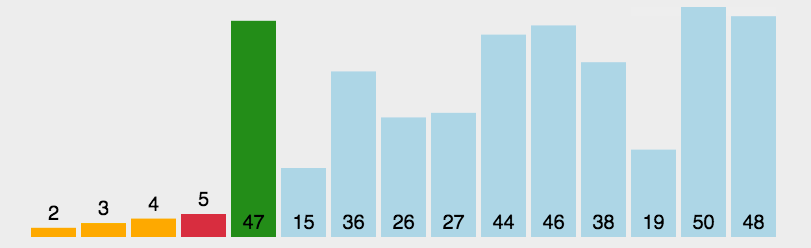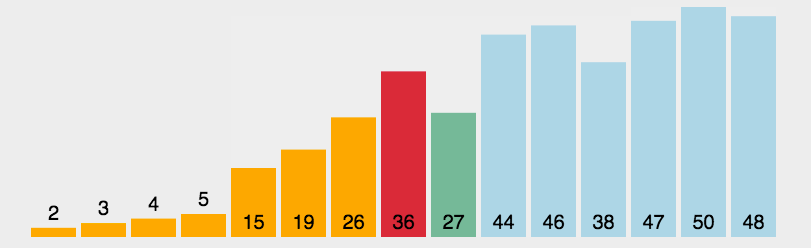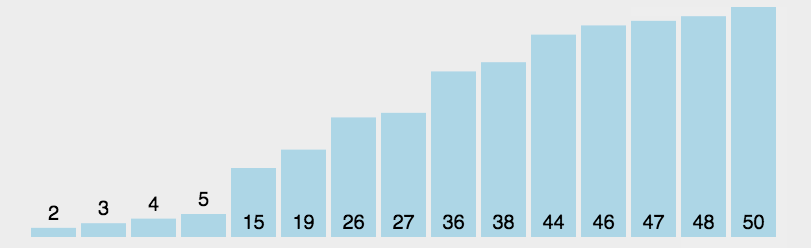
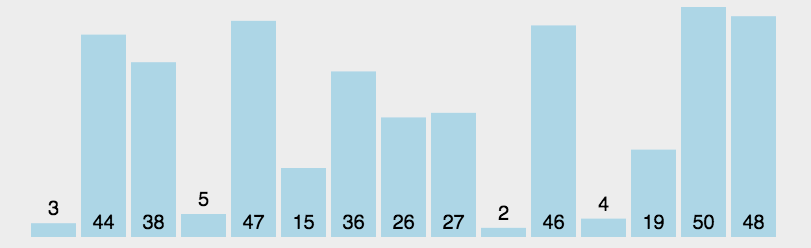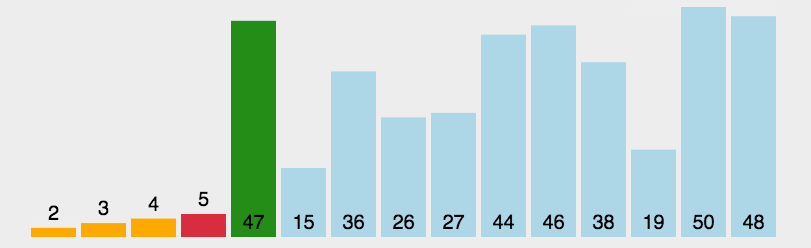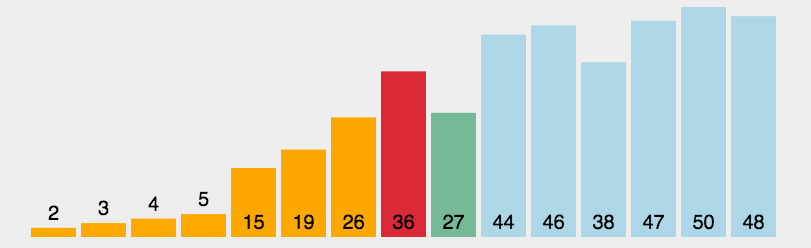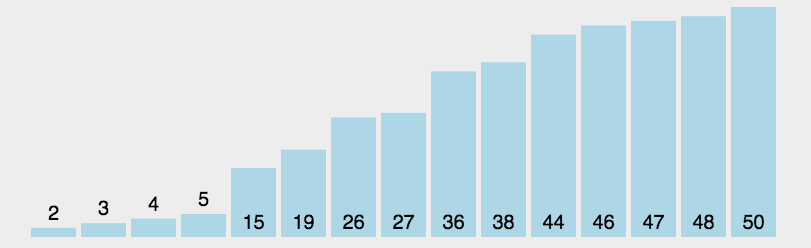
基于分治的思想。它的基本思想是通过一趟排序将待排序的记录分割成独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，然后再分别对这两部分记录进行排序，从而达到整个序列有序的目的。
步骤
详细解释
选择基准元素：从待排序序列中选择一个元素作为基准元素。一般可以选择第一个元素、最后一个元素或者随
机选择一个元素作为基准元素。
分割操作：根据基准元素，将待排序序列分割成两个子序列。一个子序列中的元素都小于基准元素，另一个子
序列中的元素都大于基准元素。这个过程称为分割操作。
递归排序：对两个子序列分别进行快速排序，直到子序列的长度为1或者0，即子序列已经有序。
合并结果：将排序好的两个子序列合并，即将左子序列、基准元素和右子序列依次拼接起来，得到最终的有序
序列。
具体步骤
选择基准元素，假设选择第一个元素作为基准元素。
设置两个指针，一个指向序列的第一个元素（左指针），一个指向序列的最后一个元素（右指针）。
左指针向右移动，直到找到一个大于基准元素的元素。
右指针向左移动，直到找到一个小于基准元素的元素。
如果左指针小于右指针，则交换这两个元素。
重复步骤3到步骤5，直到左指针大于等于右指针。
将基准元素与左指针所指的元素进行交换，此时基准元素左边的元素都小于基准元素，右边的元素都大于基
准元素。
对基准元素左边的子序列和右边的子序列分别进行递归排序。
合并结果，即将左子序列、基准元素和右子序列依次拼接起来，得到最终的有序序列。
快速排序的时间复杂度为O(nlogn)，其中n为待排序序列的长度。
举例
假设有一个待排序序列为[5, 3, 8, 2, 1, 9, 4, 7, 6]，下面以此序列为例进行快速排序。
选择基准元素：选择第一个元素5作为基准元素。
分割操作：根据基准元素5，将序列分割成两个子序列。比5小的元素放在左边，比5大的元素放在右边。
分割后的序列为[2, 1, 4, 3] 5 [9, 8, 7, 6]。
递归排序：对左右两个子序列进行递归排序。
对左子序列[2, 1, 4, 3]进行快速排序，选择基准元素2。
分割后的序列为[1] 2 [4, 3]。
对右子序列[9, 8, 7, 6]进行快速排序，选择基准元素9。
分割后的序列为[8, 7, 6] 9 []。
继续对左子序列[4, 3]进行快速排序，选择基准元素4。
分割后的序列为[3] 4 []。
对右子序列[8, 7, 6]进行快速排序，选择基准元素8。
分割后的序列为[6, 7] 8 []。
继续对左子序列[3]进行快速排序，选择基准元素3。
分割后的序列为[] 3 []。
对右子序列[6, 7]进行快速排序，选择基准元素6。
分割后的序列为[6] 7 []。
合并结果：将排序好的子序列合并。
最终的有序序列为[1, 2, 3, 4, 5, 6, 7, 8, 9]。
总结
通过以上步骤，我们可以看到快速排序将原始序列不断分割成两个子序列，并对子序列进行递归排序，最终将所
有子序列合并成一个有序序列。
复杂度分析
快速排序的时间复杂度为O(nlogn)，其中n为待排序序列的长度。
时间复杂度分析：
在最好情况下，每次分割操作都能将序列均匀地分成两部分，此时快速排序的时间复杂度为O(nlogn)。
在最坏情况下，每次分割操作都将序列分成一个较小的子序列和一个较大的子序列，此时快速排序的时间复杂
度为O(n^2)。最坏情况发生在待排序序列已经有序或基本有序的情况下。
平均情况下，快速排序的时间复杂度仍然为O(nlogn)。这是因为在每一次分割操作中，将序列分成两部分的概
率大致相等，每次分割操作的平均时间复杂度为O(n)。根据分治法的思想，快速排序的平均时间复杂度可
以近似地看作是每次分割操作的时间复杂度乘以递归的层数，即O(nlogn)。
空间复杂度分析：
快速排序的空间复杂度为O(logn)，主要是由于递归调用造成的栈空间使用。在最坏情况下，递归的层数为n，
此时空间复杂度为O(n)。在平均情况下，递归的层数为logn，此时空间复杂度为O(logn)。
文章来源：https://www.toymoban.com/news/detail-624310.html
注意
总结起来，快速排序是一种高效的排序算法，平均情况下的时间复杂度为O(nlogn)，空间复杂度为O(logn)。
但在最坏情况下，时间复杂度可能达到O(n^2)，需要额外的优化措施来避免最坏情况的发生。
应用场景
排序算法：快速排序是一种常用的排序算法，被广泛应用于各种排序任务中。它的时间复杂度较低，适用于处
理大规模数据。
数据库查询：在数据库中，经常需要对查询结果进行排序。快速排序可以在较短的时间内对查询结果进行排序，
提高查询效率。
文件系统排序：在文件系统中，需要对文件进行排序，以便更好地组织和管理文件。快速排序可以快速地对文件
进行排序，提高文件系统的性能。
搜索引擎排序：在搜索引擎中，需要对搜索结果进行排序，以便将相关度较高的结果排在前面。快速排序可以快
速地对搜索结果进行排序，提高搜索引擎的效率。
数据分析：在数据分析领域，经常需要对大量数据进行排序和统计。快速排序可以快速地对数据进行排序，为数
据分析提供支持。
文章来源地址https://www.toymoban.com/news/detail-624310.html
总结
快速排序是一种高效的排序算法，在大规模数据的排序和处理任务中具有广泛的应用场景。它的时间复杂度较
低，适用于各种需要排序的场景。
实际举例
假设有一个学生信息表，包含学生的姓名、学号和成绩。我们希望按照成绩对学生进行排序，从高到低。
快速排序可以很好地应用于这个场景。下面是一个使用快速排序对学生信息表按成绩排序的实际举例：
原始数据：假设有以下学生信息表（按成绩从高到低排列）：
学生1：姓名-张三，学号-001，成绩-90
学生2：姓名-李四，学号-002，成绩-85
学生3：姓名-王五，学号-003，成绩-95
学生4：姓名-赵六，学号-004，成绩-80
选择基准元素：选择一个基准元素，可以是任意一个学生的成绩。假设选择学生3作为基准元素。
分割操作：将学生信息表分割成两个子序列，一个序列包含所有成绩大于等于基准元素的学生，另一个序列包
含所有成绩小于基准元素的学生。
子序列1：学生3（成绩95）
子序列2：学生1（成绩90）、学生2（成绩85）、学生4（成绩80）
递归排序：对子序列1和子序列2分别进行递归排序，重复上述步骤，直到子序列只包含一个元素或为空。
合并操作：将排序后的子序列合并，得到最终的有序序列。
结果
排序后的序列：学生3（成绩95）、学生1（成绩90）、学生2（成绩85）、学生4（成绩80）
总结
通过快速排序，我们成功将学生信息表按成绩从高到低排序。这个例子展示了快速排序在实际中的应用，通过
选择基准元素、分割操作、递归排序和合并操作，可以高效地对大量数据进行排序。
代码实现
public class QuickSort {
public static void main(String[] args) {
int[] arr = {5, 2, 8, 9, 1, 3};
quickSort(arr, 0, arr.length - 1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pivotIndex = partition(arr, low, high);
quickSort(arr, low, pivotIndex - 1);
quickSort(arr, pivotIndex + 1, high);
}
}
public static int partition(int[] arr, int low, int high) {
int pivot = arr[high]; // 选择最后一个元素作为基准元素
int i = low - 1;
for (int j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return i + 1;
}
public static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
结果
输出排序后的数组。运行结果为[1, 2, 3, 5, 8, 9]，说明快速排序算法正确地对数组进行了排序。
解释
在上面的代码中，我们使用了递归的方式实现快速排序。首先定义了一个quickSort方法，接受一个数组和数组
的起始位置和结束位置作为参数。在quickSort方法中，首先判断起始位置是否小于结束位置，如果是，则
进行以下操作：
调用partition方法，将数组分割成两个子序列，并返回基准元素的索引。
对子序列1（起始位置到基准元素索引-1）和子序列2（基准元素索引+1到结束位置）分别递归调用quickSort
方法，继续进行排序。
递归结束后，数组将被排序。
在partition方法中，我们选择最后一个元素作为基准元素。然后使用两个指针i和j，从起始位置开始遍历数
组。如果遇到比基准元素小的元素，将i指针向后移动一位，并交换i和j指向的元素。遍历结束后，将基准
元素与i+1位置的元素交换，确保基准元素的位置正确。
到了这里，关于排序进行曲-v4.0的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
