一【题目类别】
- 矩阵
二【题目难度】
- 简单
三【题目编号】
- 566.重塑矩阵
四【题目描述】
- 在 MATLAB 中,有一个非常有用的函数 reshape ,它可以将一个 m x n 矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。
- 给你一个由二维数组 mat 表示的 m x n 矩阵,以及两个正整数 r 和 c ,分别表示想要的重构的矩阵的行数和列数。
- 重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。
- 如果具有给定参数的 reshape 操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。
五【题目示例】
-
示例 1:

- 输入:mat = [[1,2],[3,4]], r = 1, c = 4
- 输出:[[1,2,3,4]]
-
示例 2:

- 输入:mat = [[1,2],[3,4]], r = 2, c = 4
- 输出:[[1,2],[3,4]]
六【题目提示】
- m = = m a t . l e n g t h m == mat.length m==mat.length
- n = = m a t [ i ] . l e n g t h n == mat[i].length n==mat[i].length
- 1 < = m , n < = 100 1 <= m, n <= 100 1<=m,n<=100
- − 1000 < = m a t [ i ] [ j ] < = 1000 -1000 <= mat[i][j] <= 1000 −1000<=mat[i][j]<=1000
- 1 < = r , c < = 300 1 <= r, c <= 300 1<=r,c<=300
七【解题思路】
- 例如除法和取模的知识
- 题目要求按行优先重塑矩阵,所以我们遍历原数组的元素个数(设置为i),i对原数组的列数做除法就定位到按行优先存储的对应行数,i对原数组的列数取模就定位到按行优先存储时这一行对应的列数,这样就可以取出原数组按行优先存储时的每一个元素
- 然后将取出的元素存入创建的拥有新的行和列的新的二维数组中,在这个新的二维数组中,我们仍以刚才设置为i去寻找存入位置,i对新的二维数组的列数做除法,就得到了按行优先存储存入的行数,同理,i对新的二维数组的列数取模就定位到按行优先存储时这一行的列数,这样就可以将上一步取出来的元素存储对应位置,实现了二维数组的重塑
- 需要注意的是,如果原二维数组的元素个数不等于新的二维数组的元素的个数,直接返回原数组即可,因为无法重塑数组
- 最后返回结果即可
- PS:对于不同语言实现的细节略有不同,具体可见下面的代码
八【时间频度】
- 时间复杂度: O ( m ∗ n ) O(m * n) O(m∗n), m 、 n m、n m、n分别为传入数组的行数和列数
- 空间复杂度: O ( m ∗ n ) O(m * n) O(m∗n), m 、 n m、n m、n分别为传入数组的行数和列数
九【代码实现】
- Java语言版
class Solution {
public int[][] matrixReshape(int[][] mat, int r, int c) {
int m = mat.length;
int n = mat[0].length;
if(m * n != r * c){
return mat;
}
int[][] res = new int[r][c];
for(int i = 0;i < m * n;i++){
res[i / c][i % c] = mat[i / n][i % n];
}
return res;
}
}
- C语言版
int** matrixReshape(int** mat, int matSize, int* matColSize, int r, int c, int* returnSize, int** returnColumnSizes)
{
int m = matSize;
int n = matColSize[0];
if(m * n != r * c)
{
*returnSize = matSize;
*returnColumnSizes = matColSize;
return mat;
}
*returnSize = r;
*returnColumnSizes = (int*)malloc(sizeof(int) * r);
int** res = (int**)malloc(sizeof(int*) * r);
for(int i = 0;i < r;i++)
{
(*returnColumnSizes)[i] = c;
res[i] = (int*)malloc(sizeof(int) * c);
}
for(int i = 0;i < m * n;i++)
{
res[i / c][i % c] = mat[i / n][i % n];
}
return res;
}
- Python语言版
class Solution:
def matrixReshape(self, mat: List[List[int]], r: int, c: int) -> List[List[int]]:
m = len(mat)
n = len(mat[0])
if m * n != r * c:
return mat
res = [[0] * c for _ in range(r)]
for i in range(0,m * n):
res[i // c][i % c] = mat[i // n][i % n]
return res
- C++语言版
class Solution {
public:
vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
int m = mat.size();
int n = mat[0].size();
if(m * n != r * c){
return mat;
}
vector<vector<int>> res(r,vector<int>(c));
for(int i = 0;i < m * n;i++){
res[i / c][i % c] = mat[i / n][i % n];
}
return res;
}
};
十【提交结果】
-
Java语言版

-
C语言版

-
Python语言版
 文章来源:https://www.toymoban.com/news/detail-624460.html
文章来源:https://www.toymoban.com/news/detail-624460.html -
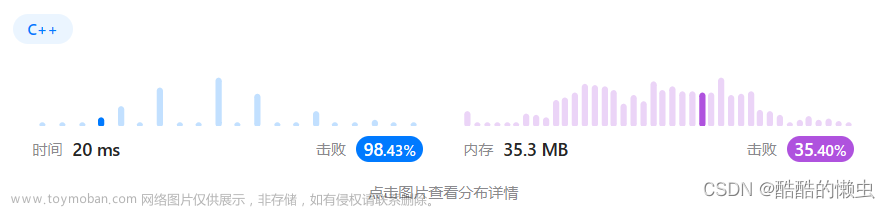
C++语言版
 文章来源地址https://www.toymoban.com/news/detail-624460.html
文章来源地址https://www.toymoban.com/news/detail-624460.html
到了这里,关于【LeetCode每日一题】——566.重塑矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!