动态规划-斐波那契数-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划-斐波那契数。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

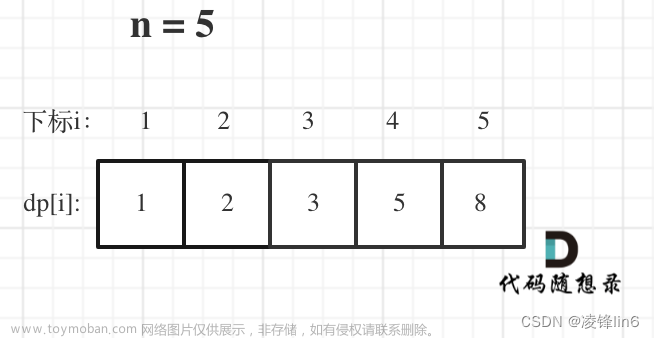
斐波那契数是一个很好的熟悉和理解动态规划的例子，通过斐波那契数可以更好的理解动态规划的精髓，动态规划是后面的计算是如何借助于前面的计算结果来加快计算速度的。

斐波那契数和斐波那契数列其实可以看成是一道题，只不过两题的限制性条件稍微有差别

1 斐波那契数

1.1 斐波那契数

斐波那契数（通常用 F(n) 表示）形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。

1.2 示例

1.2.1 示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

1.2.2 示例 2：

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

1.2.3 示例 3：

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

1.2.4 提示：

0 <= n <= 30

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/fibonacci-number
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

# 1.3 解题思路和方法

1.3.1 解题思路

如题目所说的，斐波那契数是最终是要获得f[n]的斐波那契数。
其算法转换方程如下：
F(0) = 0，F(1) = 1 /* 动态规划的边界条件 /
F(n) = F(n - 1) + F(n - 2)，其中 n > 1 / 动态规划的转移方程 */

1.3.2 代码实现

if (n < 2) 判断当前要处理的斐波那契数的id，依次来判断是做什么处理，如果是小于2，则直接依据边界条件的处理返回其值即可
如果n >= 2，则依据斐波那契数的转换方程去做处理 F(n) = F(n - 1) + F(n - 2)

class Solution {
public:
    int fib(int n) {
        if (n < 2) {
            return n;
        }
        vector<int> f(n + 1);

        f[0] = 0;
        f[1] = 1;

        for (int i = 2; i <= n; i++) {
            f[i] = f[i - 1] + f[i - 2];
        }

        return f[n];
    }
};

2 剑指 Offer 10- I. 斐波那契数列

2.1 斐波那契数列

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

2.2 示例

2.2.1 示例 1：

输入：n = 2
输出：1

2.2.2 示例 2：

输入：n = 5
输出：5

2.2.3 提示：

0 <= n <= 100文章来源地址https://www.toymoban.com/news/detail-624774.html

2.3 题解

class Solution {
    int MOD = 1000000007;
public:
    int fib(int n) {
        if (n < 2) {
            return n;
        }
        vector<int> f(n + 1);

        f[0] = 0;
        f[1] = 1;

        for (int i = 2; i <= n; i++) {
            f[i] = (f[i - 1] + f[i - 2])%MOD;
        }

        return f[n];
    }
};