二叉树的遍历（先序遍历，中序遍历，后序遍历）递归与非递归算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了二叉树的遍历（先序遍历，中序遍历，后序遍历）递归与非递归算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

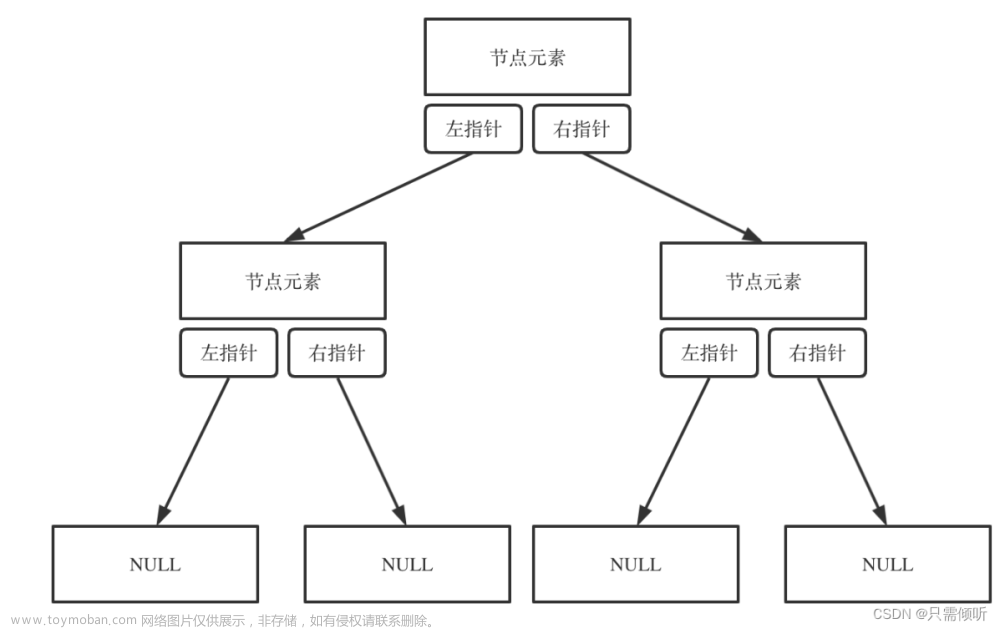
一、先序遍历

先序遍历：先遍历一颗树的根节点，后遍历左子树，最后遍历右子树

先序遍历序列： 1 -> 2 -> 4 -> 5 -> 3 -> 6 -> 7

题目链接

1.递归

分解子问题方法

class Solution {
public:
    void preOrder(TreeNode* root,vector<int>& str)
    {
        if(root==NULL)return;
        str.push_back(root->val);
        preOrder(root->left,str);
        preOrder(root->right,str);
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> str;
        preOrder(root,str);
        return str;
    }
};

二叉树的遍历（先序遍历，中序遍历，后序遍历）递归与非递归算法,leetcode,算法,c++,leetcode

2.非递归

思路：将一颗二叉树看做两个部分，一个部分是左路节点，另一个部分是左路节点的右子树，先将二叉树的左路节点全部入栈，再依次出栈，出栈的过程中将这个节点的右子树按相同方法将左路节点全部入栈，然后依次出栈，出栈的方法与上面相同，模拟递归调用的方法实现非递归，此时的入栈顺序就是先序遍历序列

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur=root;
        vector<int> v;
        while(cur||!st.empty())
        {
            //访问一棵树的开始
            //  1、访问左路节点，左路节点入栈，后续一次访问左路节点的右子树
            while(cur)
            {
                v.push_back(cur->val);
                st.push(cur);
                cur=cur->left;
            }

            //一次访问左路节点的右子树
            TreeNode* top=st.top();
            st.pop();

            //子问题的方式访问右子树
            cur=top->right;
        }
        return v;
    }
};

二、中序遍历

题目链接

中序遍历：先遍历一颗树的左子树，然后遍历根节点，最后遍历右子树

中序遍历序列：4 -> 2 -> 5 -> 1 -> 6 -> 3 -> 7

1.递归

递归调用分解子问题，与前序遍历递归思路相同

class Solution {
public:
    void inorder(TreeNode* root,vector<int>& res)
    {
        if(root==NULL)return;
        inorder(root->left,res);
        res.push_back(root->val);
        inorder(root->right,res);

    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        inorder(root,res);
        return res;
    }
};

2.非递归

与前序遍历相似，前序遍历是在入栈的顺序为前序遍历序列，而中序遍历则是出栈的顺序则为中序遍历序列

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur=root;
        vector<int> v;
        while(cur||!st.empty())
        {
            //访问一棵树的开始
            //  1、访问左路节点，左路节点入栈，后续一次访问左路节点的右子树
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            //一次访问左路节点的右子树
            TreeNode* top=st.top();
            st.pop();
            v.push_back(top->val);
            //子问题的方式访问右子树
            cur=top->right;
        }
        return v;

    }
};

三、后序遍历

后序遍历：先遍历一颗树的左子树，然后遍历右子树，最后遍历根节点

后续遍历序列：4 -> 5 -> 2 -> 6 -> 7 -> 3 -> 1

题目链接

1.递归

分解子问题

class Solution {
public:
    void postOrder(TreeNode* root,vector<int>& ret)
    {
        if(root==NULL)return;
        postOrder(root->left,ret);
        postOrder(root->right,ret);
        ret.push_back(root->val);
    }
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ret;
        postOrder(root,ret);
        return ret;
    }
};

2.非递归

后续遍历的非递归要比前序和中序遍历的非递归复杂一点，我们要在前面前序遍历和中序遍历非递归的算法上进行一些改进，创建一个变量prev，用来记录访问当前节点的上一个节点，如果当前左路节点的右子树为空或者已经访问过右子树就需将当前接节点出栈，此时的出栈顺序即为后续遍历序列。

文章来源地址https://www.toymoban.com/news/detail-624887.html

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode* cur=root;
        TreeNode* prev=NULL;
        vector<int> v;
        while(cur||!st.empty())
        {
            //访问一棵树的开始
            //  1、访问左路节点，左路节点入栈，后续一次访问左路节点的右子树
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            TreeNode* top=st.top();
            //一个节点右子树为空或者上一个访问节点是右子树的根，说明右子树访问过滤，可以访问根节点了
            if(top->right==nullptr||top->right==prev)
            {
                prev=top;
                v.push_back(top->val);
                st.pop();
            }else cur=top->right;
        }
        return v;
    }
};