PTA 1030 Travel Plan-Toy模板网

这篇具有很好参考价值的文章主要介绍了PTA 1030 Travel Plan。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

个人学习记录，代码难免不尽人意。

A traveler’s map gives the distances between cities along the highways, together with the cost of each highway. Now you are supposed to write a program to help a traveler to decide the shortest path between his/her starting city and the destination. If such a shortest path is not unique, you are supposed to output the one with the minimum cost, which is guaranteed to be unique.

Input Specification:
Each input file contains one test case. Each case starts with a line containing 4 positive integers N, M, S, and D, where N (≤500) is the number of cities (and hence the cities are numbered from 0 to N−1); M is the number of highways; S and D are the starting and the destination cities, respectively. Then M lines follow, each provides the information of a highway, in the format:

City1 City2 Distance Cost

where the numbers are all integers no more than 500, and are separated by a space.

Output Specification:
For each test case, print in one line the cities along the shortest path from the starting point to the destination, followed by the total distance and the total cost of the path. The numbers must be separated by a space and there must be no extra space at the end of output.

Sample Input:
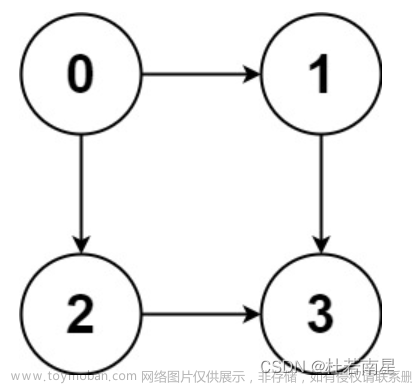
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
Sample Output:
0 2 3 3 40

#include<cstdio>
#include<algorithm>
using namespace std;
int N,M,C1,C2;
const int maxn=510;


const int INF=1000000000;
bool vis[maxn]={false};
int d[maxn],c[maxn],pre[maxn];
struct node{
	int d;
	int cost;
};
node Node[maxn][maxn];
void dijkstra(){
	fill(d,d+maxn,INF);
	fill(c,c+maxn,INF);
	for(int i=0;i<N;i++) pre[i]=i;
	d[C1]=0;c[C1]=0;
	for(int i=0;i<N;i++){
		int u=-1;int min=INF;
		for(int j=0;j<N;j++){
			if(vis[j]==false&&d[j]<min){
				u=j;
				min=d[j];
			}
		}
	if(u==-1) return;
	vis[u]=true;
	for(int v=0;v<N;v++){
		if(vis[v]==false&&Node[u][v].d!=0){
			if(d[v]>Node[u][v].d+d[u]){
				d[v]=Node[u][v].d+d[u];
				c[v]=Node[u][v].cost+c[u];
				pre[v]=u;
			}else if(d[v]==Node[u][v].d+d[u]){
				if(c[v]>Node[u][v].cost+c[u]){
					c[v]=Node[u][v].cost+c[u];
					pre[v]=u;
				}
			}
		}
	}
	}
}
void DFS(int s){
	if(s==C1){
		printf("%d",s);
		return;
	}
	else{
		DFS(pre[s]);
		printf(" %d",s);
	}
}
int main(){
	scanf("%d%d%d%d",&N,&M,&C1,&C2);
	for(int i=0;i<M;i++){
		int cost,d;
		int c1,c2;
		scanf("%d%d%d%d",&c1,&c2,&d,&cost);
		node* n=new node;
		n->cost=cost;
		n->d=d;
		Node[c1][c2]=Node[c2][c1]=*n;
		
	} 
	dijkstra();
	DFS(C2);
	printf(" %d %d\n",d[C2],c[C2]);
}

本题参考了《算法笔记》上面的dijkstra算法，对于求解这一类的最小值问题可以将dijkstra算法的模板背过，然后根据题意修改其内容即可。
除了上面这种做法还可以将第二类距离的求解从dijkstra算法中剥离出来，采用DFS方法来处理，比较简单，我觉得两种方法掌握一种即可。文章来源地址https://www.toymoban.com/news/detail-625740.html

到了这里，关于PTA 1030 Travel Plan的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！