一、图像平移

#include "opencv2/imgproc.hpp"
#include "opencv2/highgui.hpp"
#include<ctime>
#include<iostream>
using namespace cv;
using namespace std;
//平移操作,图像大小不变
Mat imageTranslation1(Mat& srcImage, int x0ffset, int y0ffset)
{
int nRows = srcImage.rows;
int nCols = srcImage.cols;
Mat resultImage(srcImage.size(), srcImage.type());
//遍历图像
for (int i = 0; i < nRows; i++)
{
for (int j = 0; j < nCols; j++)
{
int x = j - x0ffset;
int y = i - y0ffset;
//边界判断
if (x >= 0 && y >= 0 && x < nCols && y < nRows)
{
resultImage.at<Vec3b>(i, j) = srcImage.ptr<Vec3b>(y)[x];
}
}
}
return resultImage;
}
//平移操作,图形大小改变
Mat imageTranslation2(Mat& srcImage, int x0ffset, int y0ffset)
{
//设置平移尺寸
int nRows = srcImage.rows + abs(y0ffset);
int nCols = srcImage.cols + abs(x0ffset);
Mat resultImage(nRows, nCols, srcImage.type());
//图像遍历
for (int i = 0; i < nRows; i++)
{
for (int j = 0; j < nCols; j++)
{
int x = j - x0ffset;
int y = i - y0ffset;
//边界判断
if (x >= 0 && y >= 0 && x < nCols && y < nRows)
{
resultImage.at<Vec3b>(i, j) = srcImage.ptr<Vec3b>(y)[x];
}
}
}
return resultImage;
}
Mat img_shift(Mat img, int d)
{
Mat tmp;
if (d > 0)
{
//右移
Mat q0(img, Rect(0, 0, img.cols - d, img.rows));
Mat q1(img, Rect(img.cols - d, 0, d, img.rows));
q0.copyTo(tmp);
Mat q2(img, Rect(0, 0, d, img.rows));
Mat q3(img, Rect(d, 0, img.cols - d, img.rows));
q1.copyTo(q2);
tmp.copyTo(q3);
}
else
{
//左移
d = -d;
Mat q0(img, Rect(0, 0, d, img.rows));
Mat q1(img, Rect(d, 0, img.cols - d, img.rows));
q0.copyTo(tmp);
Mat q2(img, Rect(0, 0, img.cols - d, img.rows));
Mat q3(img, Rect(img.cols - d, 0, d, img.rows));
q1.copyTo(q2);
tmp.copyTo(q3);
}
return img;
}
int main()
{
//读取图像
Mat srcImage = imread("E:\\Lena.jpg");
if (srcImage.empty())
{
return -1;
}
//显示原图像
imshow("原图像", srcImage);
int x0ffset = 50;
int y0ffset = 80;
Mat resultImage1 = imageTranslation1(srcImage, x0ffset, y0ffset);
imshow("resultImage1", resultImage1);
Mat resultImage2 = imageTranslation2(srcImage, x0ffset, y0ffset);
imshow("resultImage2", resultImage2);
x0ffset = -50;
y0ffset = -80;
Mat resultImage3 = imageTranslation1(srcImage, x0ffset, y0ffset);
cv::imshow("resultImage3", resultImage3);
Mat resultImage4 = img_shift(srcImage, 60);
imshow("resultImage4", resultImage4);
cv::waitKey(0);
return 0;
}
//第二种图像平移
//将图像扩展两倍的宽 并对其进行截取达到是图像平移
Mat img_shift1(Mat img, int d)
{
Mat src(img.rows, img.cols * 2, img.type());
//水平平移 则在水平方向上对其复制粘贴
img.copyTo(src({ 0,0,img.cols,img.rows }));
img.copyTo(src({ img.cols,0,img.cols,img.rows }));
imshow("src", src);
if (d > 0)
{
Mat tmp(src, Rect(img.cols - d, 0, img.cols, img.rows));
tmp.copyTo(img);
}
else
{
Mat tmp(src, Rect(-d, 0, img.cols, img.rows));
tmp.copyTo(img);
}
return img;
}

uchar pixel_value = Mat.ptr<uchar>(row)[col]; //获取某个像素值(row行col列)
Mat.ptr<uchar>(row); //获取某行的首地址
二、图像旋转
图像旋转是指图像按照某个位置转动一定的角度的过程,旋转中图像仍保持着原始尺寸。图像旋转后图像水平对称轴、垂直对称轴及中心坐标原点都可能会发生变换,因此需要对图像旋转中的坐标进行相应转换。
2.1 求旋转矩阵
假设有一个点:P(x,y),它在绕原点 O(0,0) 旋转 β 后,被转换成 P’(x’,y’),另外,点 P 到原点 O 的距离为 r:

假设 P(x,y) 点与 X 轴成一个角α。在这里,公式如下:
x = r cos(α)
y = r sin(α)
同理,P’(x’,y’) 点将与 X 轴形成一个角,α + β。因此,公式如下:x’ = r cos(α+β)
y’ = r sin(α+β)
接下来,将使用下面的三角恒等式:cos(α+β) = cosαcosβ – sinαsinβ
现在,已经得到了前面的方程,可以把任何点变换成一个新的点,只要它旋转一个给定的角度。同样的方程可以应用于图像中的每个像素,从而得到旋转后的图像。但是,即使图像被旋转了,它仍然在一个矩形内。这意味着新图像的尺寸可以改变,而在平移中,输出图像和输入图像的尺寸保持不变。
2.2 求旋转后图像的尺寸
这里将考虑两种情况。
第一种情况是保持输出图像的尺寸与输入图像的尺寸相同。
第二种情况是修改输出图像的尺寸。
通过下面的图表来理解它们之间的区别。
将图像以逆时针方向围绕图像中心旋转一个角度 ϴ ——
左半部分显示的是即使是在旋转之后,图像的尺寸保持不变的情况
而在右半部分,缩放尺寸以覆盖整个旋转后的图像。
可以看到两种情况下得到的结果的差异。
下图中 L 和 H 为原始图像的尺寸,L' 和 H' 为旋转后的尺寸。

上图中,旋转后图像的大小,取决于图像的尺寸是保持不变还是在旋转时进行了修改。对于想要保持图像大小与初始图像大小相同的情况,只需要剔除额外的区域。如果不想保持相同的尺寸,需要学习如何获得旋转后的图像的尺寸。

2.3手工实现图像旋转
Mat imgRotate(Mat matSrc, float angle, bool direction)
{
float theta = angle * CV_PI / 180.0;
int nRowsSrc = matSrc.rows;
int nColsSrc = matSrc.cols;
// 如果是顺时针旋转
if (!direction)
theta = 2 * CV_PI - theta;
// 全部以逆时针旋转来计算
// 逆时针旋转矩阵
float matRotate[3][3]{
{std::cos(theta), -std::sin(theta), 0},
{std::sin(theta), std::cos(theta), 0 },
{0, 0, 1}
};
float pt[3][2]{
{ 0, nRowsSrc },
{nColsSrc, nRowsSrc},
{nColsSrc, 0}
};
for (int i = 0; i < 3; i++)
{
float x = pt[i][0] * matRotate[0][0] + pt[i][1] * matRotate[1][0];
float y = pt[i][0] * matRotate[0][1] + pt[i][1] * matRotate[1][1];
pt[i][0] = x;
pt[i][1] = y;
}
// 计算出旋转后图像的极值点和尺寸
float fMin_x = min(min(min(pt[0][0], pt[1][0]), pt[2][0]), (float)0.0);
float fMin_y = min(min(min(pt[0][1], pt[1][1]), pt[2][1]), (float)0.0);
float fMax_x = max(max(max(pt[0][0], pt[1][0]), pt[2][0]), (float)0.0);
float fMax_y = max(max(max(pt[0][1], pt[1][1]), pt[2][1]), (float)0.0);
int nRows = cvRound(fMax_y - fMin_y + 0.5) + 1;
int nCols = cvRound(fMax_x - fMin_x + 0.5) + 1;
int nMin_x = cvRound(fMin_x + 0.5);
int nMin_y = cvRound(fMin_y + 0.5);
// 拷贝输出图像
Mat matRet(nRows, nCols, matSrc.type(), Scalar(0));
for (int j = 0; j < nRows; j++)
{
for (int i = 0; i < nCols; i++)
{
// 计算出输出图像在原图像中的对应点的坐标,然后复制该坐标的灰度值
// 因为是逆时针转换,所以这里映射到原图像的时候可以看成是,输出图像
// 到顺时针旋转到原图像的,而顺时针旋转矩阵刚好是逆时针旋转矩阵的转置
// 同时还要考虑到要把旋转后的图像的左上角移动到坐标原点。
int x = (i + nMin_x) * matRotate[0][0] + (j + nMin_y) * matRotate[0][1];
int y = (i + nMin_x) * matRotate[1][0] + (j + nMin_y) * matRotate[1][1];
if (x >= 0 && x < nColsSrc && y >= 0 && y < nRowsSrc)
{
matRet.at<Vec3b>(j, i) = matSrc.at<Vec3b>(y, x);
}
}
}
return matRet;
}
int main()
{
Mat matSrc = imread("E:\\Lena.jpg");
if (matSrc.empty())
return 1;
float angle = 30;
Mat matRet = imgRotate(matSrc, angle, true);
imshow("src", matSrc);
imshow("rotate", matRet);
// 保存图像
imwrite("rotate_panda.jpg", matRet);
waitKey();
return 0;
}

2.4 opencv函数实现图像旋转
// 图像旋转
void Rotate(const Mat& srcImage, Mat& destImage, double angle)//angle表示要旋转的角度
{
Point2f center(srcImage.cols / 2, srcImage.rows / 2);//中心
Mat M = getRotationMatrix2D(center, angle, 1);//计算旋转的仿射变换矩阵
warpAffine(srcImage, destImage, M, Size(srcImage.cols, srcImage.rows));//仿射变换
circle(destImage, center, 2, Scalar(255, 0, 0));
}
int main()
{
//读入图像,并判断图像是否读入正确
cv::Mat srcImage = imread("E:\\Lena.jpg");
if (!srcImage.data)
{
puts("打开图像文件失败");
return -1;
}
imshow("srcImage", srcImage);
//将图片按比例缩放至宽为250像素的大小
Mat destImage;
double angle = 9.9;//角度
Rotate(srcImage, destImage, angle);
imshow("dst", destImage);
waitKey(0);
return 0;
}

旋转分为三步操作:
1. 首先,你需要得到旋转的中心。这通常是你要旋转的图像的中心。
2. 接下来,创建2d旋转矩阵。OpenCV提供了我们在上面讨论过的getRotationMatrix2D()函数。
3. 最后,使用在上一步中创建的旋转矩阵对图像应用仿射变换。OpenCV中的warpAffine()函数完成这项工作。
getRotationMatrix2D(center, angle, scale)
getRotationMatrix2D()函数接受以下参数:
center:图像的旋转中心:
angle: 旋转角度:
scale :一个各向同性的比例因子,根据提供的值将图像向上或向下缩放
如果angle是正的,图像将逆时针方向旋转。如果你想顺时针旋转图像相同的量,那么角度需要是负的。
warpAffine()函数的作用是:对图像应用一个仿射变换。在进行仿射变换后,原图像中所有的平行线在输出图像中也保持平行。
warpAffine(
src,
M,
dsize[,
dst[,
flags[,
borderMode[,
borderValue]]]]
)
函数的参数:
src:原图
M:变换矩阵
dsize:输出图像的大小
dst:输出图像
flags: 插值方法的组合如INTER_LINEAR或INTER_NEAREST
borderMode:像素扩展方法
borderValue:在边界不变的情况下使用的值,默认值为0
三、图像翻转

3.1左右翻转
//图像翻转,图像大小不变
Mat imageTranslation1(Mat& srcImage)
{
int nRows = srcImage.rows;
int nCols = srcImage.cols;
Mat resultImage(srcImage.size(), srcImage.type());
//遍历图像
for (int i = 0; i < nRows; i++)
{
for (int j = 0; j < nCols; j++)
{
resultImage.at<Vec3b>(i, j) = srcImage.at<Vec3b>(i, nCols-j-1);
}
}
return resultImage;
}
int main()
{
//读取图像
Mat srcImage = imread("E:\\Lena.jpg");
if (srcImage.empty())
{
return -1;
}
//显示原图像
imshow("原图像", srcImage);
int x0ffset = 50;
int y0ffset = 80;
Mat resultImage1 = imageTranslation1(srcImage);
imshow("resultImage1", resultImage1);
cv::waitKey(0);
return 0;
}

3.2、上下翻转
//图像翻转,图像大小不变
Mat imageTranslation1(Mat& srcImage)
{
int nRows = srcImage.rows;
int nCols = srcImage.cols;
Mat resultImage(srcImage.size(), srcImage.type());
//遍历图像
for (int i = 0; i < nRows; i++)
{
for (int j = 0; j < nCols; j++)
{
resultImage.at<Vec3b>(i, j) = srcImage.at<Vec3b>(nRows-1-i, j);
}
}
return resultImage;
}
3.3 上下颠倒,左右相反
//图像翻转,图像大小不变
Mat imageTranslation1(Mat& srcImage)
{
int nRows = srcImage.rows;
int nCols = srcImage.cols;
Mat resultImage(srcImage.size(), srcImage.type());
//遍历图像
for (int i = 0; i < nRows; i++)
{
for (int j = 0; j < nCols; j++)
{
resultImage.at<Vec3b>(i, j) = srcImage.at<Vec3b>(nRows-1-i, nCols-1-j);
}
}
return resultImage;
}

4、错切变换
图像的错切变换也称斜切,是指平面景物在投影平面上的非垂直投影,使图像中的图形在水平方向或垂直方向产生扭变。
以水平扭变为例,像素点 (x,y) 在水平方向发生扭变变成斜边,而在垂直方向的边不变,可以由以下公式描述:
4.1 实现错切变换
//图像错切
Mat imageTranslation(Mat& srcImage, float a,float b)
{
int nRows = srcImage.rows;
int nCols = srcImage.cols;
Mat resultImage(srcImage.size(), srcImage.type());
//遍历图像
for (int i = 0; i < nRows; i++)
{
for (int j = 0; j < nCols; j++)
{
if (i + a * j > 0 && i + a * j < nRows && i * b + j >0 && i * b + j< nCols)
{
resultImage.at<Vec3b>(i, j) = srcImage.at<Vec3b>( i + a * j, i * b + j);
}
}
}
return resultImage;
}

5、仿射变换
仿射变换可以理解为矩阵乘法(线性变换)和向量加法(平移)的变换。本质上,一个仿射变换代表了两个图像之间的关系,可以分别表示为:
1.旋转(线性变换)
2.平移(向量加法)
3.缩放操作(线性变换)
仿射变换通常使用2×3矩阵表示
将M乘于一个二维向量[x, y],例如图像像素坐标,最终可表示为:
5.1 求解仿射变换
仿射变换基本上是两个图像之间的关系。这种关系的信息可以通过两种方式获得:
1.已知X和T,那我们的任务就是求M;
2.已知M和X,应用T=M⋅X,得到T。
如下图:点1、2和3(在图1中形成一个三角形)被映射到图2中,仍然形成一个三角形,但现在它们已经发生了变化。如果我们找到了这3个点的仿射变换,那么我们就可以将找到的关系应用到图像中的所有像素上。

5.2 OpenCV实现仿射变换
//全局变量
String src_windowName = "原图像";
String warp_windowName = "仿射变换";
String warp_rotate_windowName = "仿射旋转变换";
String rotate_windowName = "图像旋转";
int main()
{
Point2f srcTri[3];
Point2f dstTri[3];
Mat rot_mat(2, 3, CV_32FC1);
Mat warp_mat(2, 3, CV_32FC1);
Mat srcImage, warp_dstImage, warp_rotate_dstImage, rotate_dstImage;
//加载图像
srcImage = imread("E:\\Lena.jpg");
//判断文件是否加载成功
if (srcImage.empty())
{
cout << "图像加载失败!" << endl;
return -1;
}
else
cout << "图像加载成功!" << endl << endl;
//创建仿射变换目标图像与原图像尺寸类型相同
warp_dstImage = Mat::zeros(srcImage.rows, srcImage.cols, srcImage.type());
//设置三个点来计算仿射变换
srcTri[0] = Point2f(0, 0);
srcTri[1] = Point2f(srcImage.cols - 1, 0);
srcTri[2] = Point2f(0, srcImage.rows - 1);
dstTri[0] = Point2f(srcImage.cols * 0.0, srcImage.rows * 0.33);
dstTri[1] = Point2f(srcImage.cols * 0.85, srcImage.rows * 0.25);
dstTri[2] = Point2f(srcImage.cols * 0.15, srcImage.rows * 0.7);
//计算仿射变换矩阵
warp_mat = getAffineTransform(srcTri, dstTri);
//对加载图形进行仿射变换操作
warpAffine(srcImage, warp_dstImage, warp_mat, warp_dstImage.size());
//计算图像中点顺时针旋转50度,缩放因子为0.6的旋转矩阵
Point center = Point(warp_dstImage.cols / 2, warp_dstImage.rows / 2);
double angle = -50.0;
double scale = 0.6;
//计算旋转矩阵
rot_mat = getRotationMatrix2D(center, angle, scale);
//旋转已扭曲图像
warpAffine(warp_dstImage, warp_rotate_dstImage, rot_mat, warp_dstImage.size());
//将原图像旋转
warpAffine(srcImage, rotate_dstImage, rot_mat, srcImage.size());
//显示变换结果
namedWindow(src_windowName, WINDOW_AUTOSIZE);
imshow(src_windowName, srcImage);
namedWindow(warp_windowName, WINDOW_AUTOSIZE);
imshow(warp_windowName, warp_dstImage);
namedWindow(warp_rotate_windowName, WINDOW_AUTOSIZE);
imshow(warp_rotate_windowName, warp_rotate_dstImage);
namedWindow(rotate_windowName, WINDOW_AUTOSIZE);
imshow(rotate_windowName, rotate_dstImage);
waitKey(0);
return 0;
}

5.3手动
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace std;
using namespace cv;
#define PI 3.1415927
#define MAX(a,b) (((a)>(b))?(a):(b))
// 单点双线性插值
// [输入] ii--dst的行索引
// jj--dst的列索引
// u_src--jj反向映射到src中对应的列索引
// v_src--ii反向映射到src中对应的行索引
int Bilinear_interpolation_img(Mat src, Mat& dst, int ii, int jj, double u_src, double v_src)
{
if (src.rows <= 0 || src.cols <= 0 ||
(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
{
printf("输入图像有误!\n");
return 0;
}
if (u_src >= 0 && u_src <= src.cols - 1 && v_src >= 0 && v_src <= src.rows - 1)
{
int x1 = int(u_src), x2 = (int)(u_src + 0.5), y1 = (int)v_src, y2 = (int)(v_src + 0.5);
double pu = fabs(u_src - x1), pv = fabs(v_src - y2);
if (src.channels() == 1)
{
dst.at<uchar>(ii, jj) = (1 - pv) * (1 - pu) * src.at<uchar>(y2, x1) +
(1 - pv) * pu * src.at<uchar>(y2, x2) +
pv * (1 - pu) * src.at<uchar>(y1, x1) + pv * pu * src.at<uchar>(y1, x2);
}
else
{
dst.at<Vec3b>(ii, jj)[0] = (1 - pv) * (1 - pu) * src.at<Vec3b>(y2, x1)[0] +
(1 - pv) * pu * src.at<Vec3b>(y2, x2)[0] +
pv * (1 - pu) * src.at<Vec3b>(y1, x1)[0] +
pv * pu * src.at<Vec3b>(y1, x2)[0];
dst.at<Vec3b>(ii, jj)[1] = (1 - pv) * (1 - pu) * src.at<Vec3b>(y2, x1)[1] +
(1 - pv) * pu * src.at<Vec3b>(y2, x2)[1] +
pv * (1 - pu) * src.at<Vec3b>(y1, x1)[1] +
pv * pu * src.at<Vec3b>(y1, x2)[1];
dst.at<Vec3b>(ii, jj)[2] = (1 - pv) * (1 - pu) * src.at<Vec3b>(y2, x1)[2] +
(1 - pv) * pu * src.at<Vec3b>(y2, x2)[2] +
pv * (1 - pu) * src.at<Vec3b>(y1, x1)[2] +
pv * pu * src.at<Vec3b>(y1, x2)[2];
}
}
return 1;
}
//水平镜像、垂直镜像变换
// [输入] way_mirror镜像方法:0水平镜像 1垂直镜像
int affine_mirrorImg(Mat src, Mat& dst, int way_mirror)
{
if (src.rows <= 0 || src.cols <= 0 ||
(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U) {
printf("输入图像有误!\n");
return 0;
}
if (way_mirror != 0 && way_mirror != 1) {
printf("输入镜像方法不为1或0,way_mirror: %d!\n", way_mirror);
return 0;
}
int dst_h = src.rows, dst_w = src.cols;//目标图像宽高 初始化为原图宽高
int ii = 0, jj = 0;
double u_src = 0, v_src = 0;
Mat M_mirr = (Mat_<double>(3, 3) << -1, 0, 0, 0, 1, 0, 0, 0, 1);
if (way_mirror) {
M_mirr.at<double>(0, 0) = 1;
M_mirr.at<double>(1, 1) = -1;
}
Mat M_corrToSrc = (Mat_<double>(3, 3) << 1, 0, src.cols, 0, 1, 0, 0, 0, 1);
if (way_mirror) {
M_corrToSrc.at<double>(0, 2) = 0;
M_corrToSrc.at<double>(1, 2) = src.rows;
}
Mat M_trans = M_corrToSrc * M_mirr;
Mat M_trans_inv = M_trans.inv();
Mat dst_uv(3, 1, CV_64F);
dst_uv.at<double>(2, 0) = 1;
Mat src_uv(dst_uv);
if (src.channels() == 3)
dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC3); //RGB图初始
else
dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC1);
//反向映射
for (ii = 0; ii < dst_h; ++ii)
{
for (jj = 0; jj < dst_w; ++jj)
{
dst_uv.at<double>(0, 0) = jj;
dst_uv.at<double>(1, 0) = ii;
src_uv = M_trans_inv * dst_uv;
u_src = src_uv.at<double>(0, 0);
v_src = src_uv.at<double>(1, 0);
// 边界问题
if (u_src < 0) u_src = 0;
if (v_src < 0) v_src = 0;
if (u_src > src.cols - 1) u_src = src.cols - 1;
if (v_src > src.rows - 1) v_src = src.rows - 1;
//双线性插值
Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);
}
}
return 1;
}
// 图像旋转(绕图像中心) 逆时针旋转为正
// 可处理8位单通道或三通道图像
int affine_rotateImg(Mat src, Mat& dst, double Angle)
{
if (src.rows <= 0 || src.cols <= 0 ||
(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
{
printf("输入图像有误!\n");
return 0;
}
double angle = 0, cos_a = 0, sin_a = 0;//旋转角度
int dst_h = src.rows, dst_w = src.cols;//目标图像宽高 初始化为原图宽高
int ii = 0, jj = 0;
double u_src = 0, v_src = 0;
angle = Angle / 180 * CV_PI;
cos_a = cos(angle);
sin_a = sin(angle);
dst_h = (int)(fabs(src.rows * cos_a) + fabs(src.cols * sin_a) + 0.5);
dst_w = (int)(fabs(src.rows * sin_a) + fabs(src.cols * cos_a) + 0.5);
if (src.channels() == 3)
{
dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC3); //RGB图初始
}
else
{
dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC1);
}
Mat M_toPhysics = (Mat_<double>(3, 3) << 1, 0, -0.5 * src.cols, 0, -1, 0.5 * src.rows, 0, 0, 1);
Mat M_rotate = (Mat_<double>(3, 3) << cos_a, -sin_a, 0, sin_a, cos_a, 0, 0, 0, 1);
Mat M_toPixel = (Mat_<double>(3, 3) << 1, 0, 0.5 * dst.cols, 0, -1, 0.5 * dst.rows, 0, 0, 1);
Mat M_trans = M_toPixel * M_rotate * M_toPhysics;
Mat M_trans_inv = M_trans.inv();
Mat dst_uv(3, 1, CV_64F);
dst_uv.at<double>(2, 0) = 1;
Mat src_uv(dst_uv);
//反向映射
for (ii = 0; ii < dst_h; ++ii)
{
for (jj = 0; jj < dst_w; ++jj)
{
dst_uv.at<double>(0, 0) = jj;
dst_uv.at<double>(1, 0) = ii;
src_uv = M_trans_inv * dst_uv;
u_src = src_uv.at<double>(0, 0);
v_src = src_uv.at<double>(1, 0);
//处理边界问题
if (int(Angle) % 90 == 0)
{
if (u_src < 0) u_src = 0;
if (v_src < 0) v_src = 0;
if (u_src > src.cols - 1) u_src = src.cols - 1;
if (v_src > src.rows - 1) v_src = src.rows - 1;
}
//双线性插值
Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);
}
}
return 1;
}
// 图像平移 在像素坐标系下进行 图像左顶点为原点,x轴为图像列,y轴为图像行
// tx: x方向(图像列)平移量,向右平移为正
// ty: y方向(图像行)平移量,向下平移为正
int affine_moveImg(Mat src, Mat& dst, double tx, double ty)
{
if (src.rows <= 0 || src.cols <= 0 ||
(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
{
printf("输入图像有误!\n");
return 0;
}
int dst_h = src.rows, dst_w = src.cols;
int ii = 0, jj = 0;
double u_src = 0, v_src = 0;
if (src.channels() == 3)
{
dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC3); //RGB图初始
}
else
{
dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC1);
}
Mat M_toPhysics = (Mat_<double>(3, 3) << 1, 0, tx, 0, 1, ty, 0, 0, 1);
Mat M_trans_inv = M_toPhysics.inv();
Mat dst_uv(3, 1, CV_64F);
dst_uv.at<double>(2, 0) = 1;
Mat src_uv(dst_uv);
//反向映射
for (ii = 0; ii < dst_h; ++ii)
{
for (jj = 0; jj < dst_w; ++jj)
{
dst_uv.at<double>(0, 0) = jj;
dst_uv.at<double>(1, 0) = ii;
src_uv = M_trans_inv * dst_uv;
u_src = src_uv.at<double>(0, 0);
v_src = src_uv.at<double>(1, 0);
//双线性插值
Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);
}
}
return 1;
}
// 缩放 以图像左顶点为原点
// cx: 水平缩放尺度
// cy: 垂直缩放尺度
int affine_scalingImg(Mat src, Mat& dst, double cx, double cy)
{
if (src.rows <= 0 || src.cols <= 0 ||
(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
{
printf("输入图像有误!\n");
return 0;
}
int dst_h = (int)(cy * src.rows + 0.5), dst_w = (int)(cx * src.cols + 0.5);
int ii = 0, jj = 0;
double u_src = 0, v_src = 0;
if (src.channels() == 3)
{
dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC3); //RGB图初始
}
else
{
dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC1);
}
Mat M_scale = (Mat_<double>(3, 3) << cx, 0, 0, 0, cy, 0, 0, 0, 1);
Mat M_trans_inv = M_scale.inv();
Mat dst_uv(3, 1, CV_64F);
dst_uv.at<double>(2, 0) = 1;
Mat src_uv(dst_uv);
//反向映射
for (ii = 0; ii < dst_h; ++ii)
{
for (jj = 0; jj < dst_w; ++jj)
{
dst_uv.at<double>(0, 0) = jj;
dst_uv.at<double>(1, 0) = ii;
src_uv = M_trans_inv * dst_uv;
u_src = src_uv.at<double>(0, 0);
v_src = src_uv.at<double>(1, 0);
// 边界问题
if (u_src < 0) u_src = 0;
if (v_src < 0) v_src = 0;
if (u_src > src.cols - 1) u_src = src.cols - 1;
if (v_src > src.rows - 1) v_src = src.rows - 1;
//双线性插值
Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);
}
}
return 1;
}
// 错切变换 以图像中心为偏移中心
// [输入] sx--水平错切系数
// sy--垂直错切系数
int affine_miscut(Mat src, Mat& dst, double sx, double sy)
{
if (src.rows <= 0 || src.cols <= 0 ||
(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
{
printf("输入图像有误!\n");
return 0;
}
int dst_h = fabs(sy) * src.cols + src.rows, dst_w = fabs(sx) * src.rows + src.cols;
int ii = 0, jj = 0;
double u_src = 0, v_src = 0;
if (src.channels() == 3)
{
dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC3); //RGB图初始
}
else
{
dst = cv::Mat::zeros(dst_h, dst_w, CV_8UC1);
}
Mat M_toPhysics = (Mat_<double>(3, 3) << 1, 0, -0.5 * src.cols, 0, -1, 0.5 * src.rows, 0, 0, 1);
Mat M_rotate = (Mat_<double>(3, 3) << 1, sx, 0, sy, 1, 0, 0, 0, 1);
Mat M_toPixel = (Mat_<double>(3, 3) << 1, 0, 0.5 * dst.cols, 0, -1, 0.5 * dst.rows, 0, 0, 1);
Mat M_trans = M_toPixel * M_rotate * M_toPhysics;
Mat M_trans_inv = M_trans.inv();
Mat dst_uv(3, 1, CV_64F);
dst_uv.at<double>(2, 0) = 1;
Mat src_uv(dst_uv);
//反向映射
for (ii = 0; ii < dst_h; ++ii)
{
for (jj = 0; jj < dst_w; ++jj)
{
dst_uv.at<double>(0, 0) = jj;
dst_uv.at<double>(1, 0) = ii;
src_uv = M_trans_inv * dst_uv;
u_src = src_uv.at<double>(0, 0);
v_src = src_uv.at<double>(1, 0);
//双线性插值
Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);
}
}
return 1;
}
// 组合变换示例
// 缩放->旋转->错切(即偏移)
// [输入]
int affine_srm_combImg(Mat src, Mat& dst, double cx, double cy, double Angle, double sx, double sy)
{
if (src.rows <= 0 || src.cols <= 0 ||
(src.channels() != 1 && src.channels() != 3) || src.depth() != CV_8U)
{
printf("输入图像有误!\n");
return 0;
}
double angle, cos_a, sin_a;
int dst_s_h, dst_s_w, dst_sr_h, dst_sr_w, dst_srm_h, dst_srm_w;
angle = Angle / 180 * CV_PI;
cos_a = cos(angle);
sin_a = sin(angle);
dst_s_h = (int)(cy * src.rows + 0.5);
dst_s_w = (int)(cx * src.cols + 0.5);
dst_sr_h = (int)(fabs(dst_s_h * cos_a) + fabs(dst_s_w * sin_a) + 0.5);
dst_sr_w = (int)(fabs(dst_s_h * sin_a) + fabs(dst_s_w * cos_a) + 0.5);
dst_srm_h = fabs(sy) * dst_sr_w + dst_sr_h;
dst_srm_w = fabs(sx) * dst_sr_h + dst_sr_w;
int ii = 0, jj = 0;
double u_src = 0, v_src = 0;
if (src.channels() == 3)
{
dst = cv::Mat::zeros(dst_srm_h, dst_srm_w, CV_8UC3); //RGB图初始
}
else
{
dst = cv::Mat::zeros(dst_srm_h, dst_srm_w, CV_8UC1);
}
Mat M_scale = (Mat_<double>(3, 3) << cx, 0, 0, 0, cy, 0, 0, 0, 1);
Mat M_toPhysics = (Mat_<double>(3, 3) << 1, 0, -0.5 * dst_s_w, 0, -1, 0.5 * dst_s_h, 0, 0, 1);
Mat M_rotate = (Mat_<double>(3, 3) << cos_a, -sin_a, 0, sin_a, cos_a, 0, 0, 0, 1);
Mat M2 = M_rotate * M_toPhysics;
Mat M_mis = (Mat_<double>(3, 3) << 1, sx, 0, sy, 1, 0, 0, 0, 1);
Mat M_toPixel = (Mat_<double>(3, 3) << 1, 0, 0.5 * dst.cols, 0, -1, 0.5 * dst.rows, 0, 0, 1);
Mat M3 = M_toPixel * M_mis;
Mat M_trans = M3 * M2 * M_scale;
Mat M_trans_inv = M_trans.inv();
Mat dst_uv(3, 1, CV_64F);
dst_uv.at<double>(2, 0) = 1;
Mat src_uv(dst_uv);
//反向映射
for (ii = 0; ii < dst_srm_h; ++ii)
{
for (jj = 0; jj < dst_srm_w; ++jj)
{
dst_uv.at<double>(0, 0) = jj;
dst_uv.at<double>(1, 0) = ii;
src_uv = M_trans_inv * dst_uv;
u_src = src_uv.at<double>(0, 0);
v_src = src_uv.at<double>(1, 0);
//处理边界问题
if (int(Angle) % 90 == 0)
{
if (u_src < 0) u_src = 0;
if (v_src < 0) v_src = 0;
if (u_src > src.cols - 1) u_src = src.cols - 1;
if (v_src > src.rows - 1) v_src = src.rows - 1;
}
//双线性插值
Bilinear_interpolation_img(src, dst, ii, jj, u_src, v_src);
}
}
return 1;
}
int main()
{
Mat src = imread("E:\\Lena.jpg", 1), dst;
//水平、垂直镜像
int way_mirror = 1;
//affine_mirrorImg(src, dst, way_mirror);
//旋转
double angle_r = 250;
//int flag = affine_rotateImg(src, dst, angle_r);
//if (flag == 0)
//{
// return;
//}
//平移
double tx = 50, ty = -50;
// affine_moveImg(src, dst, tx, ty);
//尺度变换(缩放)
double cx = 1.5, cy = 1.5;
affine_scalingImg(src, dst, cx, cy);
//错切(偏移)
double sx = 0.2, sy = 0.2;
//affine_trans_deviation(src, dst, sx, sy);
affine_miscut(src, dst, sx, sy);
//组合变换 缩放->旋转->错切(即偏移)
//affine_srm_combImg(src, dst, cx, cy, angle_r, sx, sy);
// 显示
Mat src_resize, dst_resize;
//affine_scalingImg(src, src_resize, 0.4, 0.3);
//affine_scalingImg(dst, dst_resize, 0.4, 0.3);
namedWindow("src", 0);
namedWindow("dst", 0);
imshow("src", src);
imshow("dst", dst);
waitKey(0);
system("pause");
return 0;
}
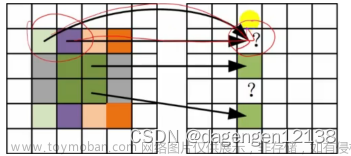
6、图像缩放
图像可以通过两种方式调整大小:
假设图像的初始尺寸为 W×H,其中 W 和 H 分别代表宽度和高度。如果想要加倍的大小(尺寸)的图像,可以调整或缩放图像到 2W×2H。类似地,如果想将图像的大小(尺寸)减少一半,那么可以调整或缩放图像到W/2×H/2。因为只是想缩放图像,可以在调整大小时传递缩放因子(长度和宽度),图像输出尺寸可以根据这些比例因子计算出来。
同时,也可能想要将图像的大小调整为一个固定的尺寸,比如 420×360像素。在这种情况下,缩放将不起作用,因为不能确定初始维度是固定维度的倍数(或因数)。这要求在调整大小时直接传递图像的新尺寸。

上图显示了想要调整大小的图像和像素值。目前,它的尺寸是 5×5。假设我们想要翻倍。这将导致以下输出。但是,我们想要填充像素值。
让我们看看我们有哪些不同的选择。可以复制像素。这将给我们如下图所示的结果:
如果去掉前面图像中的像素值(方格里面的数字),将得到如下图所示的图像。将其与原始图像进行比较。注意它看起来和原始图像是多么的相似
类似地,如果想要将图像缩小一半,可以减少一些像素。你会注意到,在调整大小时,复制了像素。还可以使用其他一些技巧。譬如:可以使用插值,即根据相邻像素的像素值找出新的像素值,而不是直接复制它们。这给了颜色一个很好的平滑过渡。下图显示了如果我们使用不同的插值,结果是如何变化的。从下图中,可以看到,当从左到右执行时,新创建的像素值的计算方式是不同的。在前三幅图像中,像素是直接从相邻像素复制的,而在后一幅图像中,像素值依赖于所有相邻像素(左、右、上、下),也依赖于对角线相邻的像素:
6.1 实现图像缩放
//图像缩小
Mat imageTranslation(Mat& srcImage,int n)
{
int nRows = srcImage.rows;
int nCols = srcImage.cols;
Mat resultImage(srcImage.size() / n, srcImage.type());
//遍历图像
for (int i = 0; i < nRows; i++)
{
for (int j = 0; j < nCols; j++)
{
if (n * i < nRows && n * j < nCols)
{
resultImage.at<Vec3b>(i, j) = srcImage.at<Vec3b>(n * i, n * j);
}
}
}
return resultImage;
}
//图像放大
Mat imageTranslation1(Mat& srcImage, int n)
{
int nRows = srcImage.rows;
int nCols = srcImage.cols;
Mat resultImage(srcImage.size() * n, srcImage.type());
//遍历图像
for (int i = 0; i < nRows * n; i++)
{
for (int j = 0; j < nCols * n ; j++)
{
resultImage.at<Vec3b>(i, j) = srcImage.at<Vec3b>( i / n , j / n);
}
}
return resultImage;
}
int main()
{
//读取图像
Mat srcImage = imread("E:\\Lena.jpg");
if (srcImage.empty())
{
return -1;
}
//显示原图像
imshow("原图像", srcImage);
int x0ffset = 50;
int y0ffset = 80;
int n = 2;
Mat resultImage1 = imageTranslation(srcImage,n);
imshow("缩小图片", resultImage1);
Mat resultImage2 = imageTranslation1(srcImage, n);
imshow("放大图片", resultImage2);
cv::waitKey(0);
return 0;
}

Mat imgDown_1(Mat& srcimg, float kx, float ky)
{
//提取图像的分辨率
int nrows = cvRound(srcimg.rows * kx);
int ncols = cvRound(srcimg.cols * ky);
Mat resimg(nrows, ncols, srcimg.type());
for (int i = 0; i < nrows; i++)
{
for (int j = 0; j < ncols; j++)
{
//根据水平因子计算坐标
int x = static_cast<int>((i + 1) / kx + 0.5) - 1;
//根据垂直因子计算坐标
int y = static_cast<int>((j + 1) / ky + 0.5) - 1;
resimg.at<Vec3b>(i, j) = srcimg.at<Vec3b>(x, y);
}
}
return resimg;
}
//对图像进行放大
Mat imgUp_1(Mat& srcimg, float kx, float ky)
{
int nrows = srcimg.rows * kx;
int ncols = srcimg.cols * ky;
Mat resimg(nrows, ncols, srcimg.type());
for (int i = 0; i < nrows; i++)
{
//int x = i / kx;
int x = static_cast<int>((i + 1) / kx + 0.7) - 1;
for (int j = 0; j < ncols; j++)
{
//int y = j / ky;
int y = static_cast<int>((j + 1) / ky + 0.7) - 1;
resimg.at<Vec3b>(i, j) = srcimg.at<Vec3b>(x, y);
}
}
return resimg;
}
Vec3b areaAverage(const Mat& srcimg, Point_<int> leftPoint, Point_<int> rightPoint)
{
int tmp1 = 0, tmp2 = 0, tmp3 = 0;
//计算区域字块像素点个数
int nPix = (rightPoint.x - leftPoint.x + 1) * (rightPoint.y - leftPoint.y + 1);
//对区域字块各个通道对像素值求和
for (int i = leftPoint.x; i <= rightPoint.x; i++)
{
for (int j = leftPoint.y; j <= rightPoint.y; j++)
{
tmp1 += srcimg.at<Vec3b>(i, j)[0];
tmp2 += srcimg.at<Vec3b>(i, j)[1];
tmp3 += srcimg.at<Vec3b>(i, j)[2];
}
}
//对每个通道求均值
Vec3b vecTmp;
vecTmp[0] = tmp1 / nPix;
vecTmp[1] = tmp2 / nPix;
vecTmp[2] = tmp3 / nPix;
return vecTmp;
}
Mat imgDown_2(const Mat& srcimg, double kx, double ky)
{
int nrows = srcimg.rows * kx;
int ncols = srcimg.cols * ky;
/*
int nrows = cvRound(srcimg.rows * kx);
int ncols = cvRound(srcimg.cols * ky);
*/
Mat resimg(nrows, ncols, srcimg.type());
//区域子块的左上角行列坐标
int leftRowCoordinate = 0;
int leftColCoordinate = 0;
for (int i = 0; i < nrows; i++)
{
//根据水平因子计算坐标
int x = static_cast<int>((i + 1) / kx + 0.5) - 1;
for (int j = 0; j < ncols; j++)
{
//根据垂直因子计算坐标
int y = static_cast<int>((j + 1) / ky + 0.5) - 1;
//求解区域子块的均值
resimg.at<Vec3b>(i, j) = areaAverage(srcimg, Point_<int>(leftRowCoordinate, leftColCoordinate), Point_<int>(x, y));
//resimg.at<Vec3b>(i, j) = srcimg.at<Vec3b>(x, y);
//更新下子块左上角的列坐标,行坐标不变
leftColCoordinate = y + 1;
}
leftColCoordinate = 0;
//更新下子块左上角的行坐标
leftRowCoordinate = x + 1;
}
return resimg;
}
//对图像进行放大
Mat imgUp_2(const Mat& srcimg, double kx, double ky)
{
int nrows = srcimg.rows * kx;
int ncols = srcimg.cols * ky;
Mat resimg(nrows, ncols, srcimg.type());
int leftRowCoordinate = 0;
int leftColCoordinate = 0;
for (int i = 0; i < nrows; i++)
{
int x = i / kx;
for (int j = 0; j < ncols; j++)
{
int y = j / ky;
//resimg.at<Vec3b>(i, j) = areaAverage(srcimg, Point_<int>(leftRowCoordinate, leftColCoordinate), Point_<int>(x, y));
resimg.at<Vec3b>(i, j) = srcimg.at<Vec3b>(x, y);
leftColCoordinate = y + 1;
}
leftColCoordinate = 0;
leftRowCoordinate = x + 1;
}
return resimg;
}
int main()
{
//Mat srcimg = imread("C:\\Users\\H\\Desktop\\1.png");
Mat srcimg = imread("E:\\Lena.jpg");
if (srcimg.empty())
{
return -1;
}
imshow("srcimg", srcimg);
//自定义图像缩放模式
Mat upimg1 = imgUp_1(srcimg, 2, 2);
imshow("upimg1", upimg1);
Mat resimg1 = imgDown_1(srcimg, 0.5, 0.5);
imshow("resimg1", resimg1);
Mat resimg2 = imgDown_2(srcimg, 0.5, 0.5);
imshow("resimg2", resimg2);
Mat upimg2 = imgUp_2(srcimg, 2, 2);
imshow("upimg2", upimg2);
//图像金子塔实现图像的缩放
Mat pyrDownimg;
pyrDown(srcimg, pyrDownimg);
imshow("pyrDownimg", pyrDownimg);
Mat pyrUpimg;
pyrUp(srcimg, pyrUpimg);
imshow("pyrUpimg", pyrUpimg);
//resize方式实现图像的缩放
Mat dstimg;
const double scaleVal = 2;
//resize(srcimg, dstimg, Size(srcimg.cols*0.5, srcimg.rows*0.5));
resize(srcimg, dstimg, Size(srcimg.cols * 2, srcimg.rows * 2));
imshow("dstimg", dstimg);
waitKey(0);
return 0;
}

7.透视变换
仿射变换后依然是平行四边形,并不能做到任意的变换。
#7.1 透视变换原理
透视变换(Perspective Transformation)是将二维的图片投影到一个三维视平面上,然后再转换到二维坐标下,所以也称为投影映射(Projective Mapping)。简单来说就是二维→三维→二维的一个过程。
透视变换公式:

透视变换矩阵表示:
仿射变换是透视变换的子集。接下来再通过除以Z轴转换成二维坐标:
透视变换中的三维->二维
透视变换相比仿射变换更加灵活,变换后会产生一个新的四边形,但不一定是平行四边形,所以需要非共线的四个点才能唯一确定,原图中的直线变换后依然是直线。因为四边形包括了所有的平行四边形,所以透视变换包括了所有的仿射变换。文章来源:https://www.toymoban.com/news/detail-626861.html
7.2 实现透视变换
int main() {
string path = "E:\\Lena.jpg";
Mat img = imread(path);
float w = 150, h = 250;
Mat matrix, imgWarp;
Point2f src[4] = { {96,94},{212,94},{96,209},{212,209} };
Point2f dst[4] = { {0.0f,0.0f},{w,0.0f},{0.0f,h},{w,h} };
matrix = getPerspectiveTransform(src, dst);
warpPerspective(img, imgWarp, matrix, Point(w, h));
for (int i = 0; i < 4; i++)
{
circle(img, src[i], 10, Scalar(0, 0, 255), FILLED);
}
imshow("Image", img);
imshow("Image Warp", imgWarp);
waitKey(0);
return 0;
}
 文章来源地址https://www.toymoban.com/news/detail-626861.html
文章来源地址https://www.toymoban.com/news/detail-626861.html
(1)Mat getPerspectiveTransform(const Point2f* src, const Point2f* dst)
//参数const Point2f* src:原图的四个固定顶点
//参数const Point2f* dst:目标图像的四个固定顶点
//返回值:Mat型变换矩阵,可直接用于warpAffine()函数
//注意,顶点数组长度超4个,则会自动以前4个为变换顶点;数组可用Point2f[]或Point2f*表示
//注意:透视变换的点选取变为4个
(2)C++ void warpPerspective(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())
//参数InputArray src:输入变换前图像
//参数OutputArray dst:输出变换后图像,需要初始化一个空矩阵用来保存结果,不用设定矩阵尺寸
//参数InputArray M:变换矩阵,用另一个函数getAffineTransform()计算
//参数Size dsize:设置输出图像大小
//参数int flags = INTER_LINEAR:设置插值方式,默认方式为线性插值(另一种WARP_FILL_OUTLIERS)
到了这里,关于Opencv-C++笔记 (16) : 几何变换 (图像的翻转(镜像),平移,旋转,仿射,透视变换)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!