基于Verilog HDL的FFT算法硬件实现（8点，三级流水线，DIT-FFT）-Toy模板网

这篇具有很好参考价值的文章主要介绍了基于Verilog HDL的FFT算法硬件实现（8点，三级流水线，DIT-FFT）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

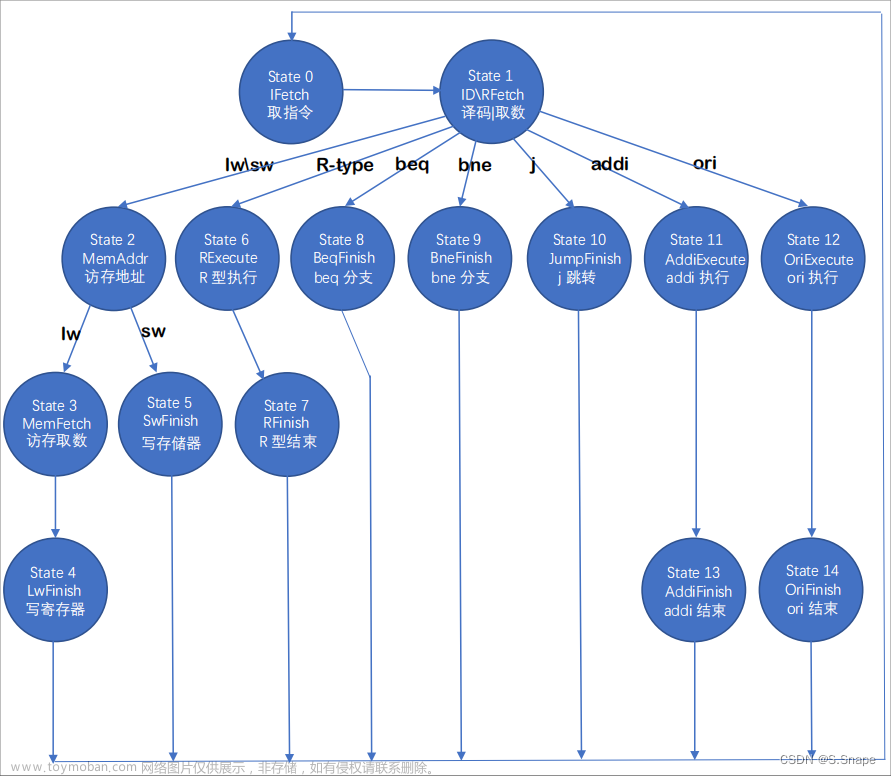
1.原理

关于fft的相关知识，在之前的文章中，有过介绍，这里不再具体介绍，可以参考学习。

从傅里叶级数（FS）到傅里叶变换(FT)最后到离散傅里叶变换（DFT）_小张爱学习哦的博客-CSDN博客_fs傅里叶级数

FFT原理（基2DIT-FFT）及C语言编程思路及实现_小张爱学习哦的博客-CSDN博客_c语言实现fft原理

verilog实现fft,数字信号处理,算法,硬件工程,学习,傅立叶分析

总结下来：就是要硬件实现上图这个蝶形流图。

2.硬件需要考虑的问题及处理思路

关于旋转因子问题：旋转因子是一个复数运算，可以通过欧拉公式转换成实部虚部分别为两个三角函数的值。对于已知点数的蝶形图，旋转因子具体值是已知的，因此，可以通过前期使用matlab计算出来，这样就可以减少硬件的运算量和电路复杂度。
关于旋转因子存储问题：可以知道旋转因子的实部和虚部是两个三角函数的值，因此是一个大于-1，小于的的数，说明这个数如果直接存储则需要使用小数存储。而小数如果用硬件存储，我们知道需要使用浮点存储（一般使用IEEE 754这个存储方案）。问题是，如果这样存储，则所有的运算都变成浮点运算，进一步加大电路复杂度。

处理思路：如果将旋转因子扩大很多倍，我们在后续只要保证整个式子的正确性，最终结果相当于也是扩大相同倍数，最后我们只需要把最终结果缩小相同倍数就是正确答案了。（一般扩大的倍数选择2的整数次方，因为咱硬件中处理简单，相当于移位操作）。我这里将旋转因子扩大8192倍，也就是2的13次方倍，电路处理时只需要将结果左移13位。（同时需要注意，这里的移位都是对有符号的数进行移位，因此要注意符号位处理）。
关于流水线的问题：对于8点的fft我们知道需要三级蝶形运算，每一级蝶形运算从运算量上来说是相同的。如果不使用流水线，我们只需要一套计算蝶形运算的电路就可以，这样电路规模会减少很多，但带来的问题是计算一次结果所需要的时间增多。那如果是16点fft则需要4级蝶形运算，如果是1024点那？计算结果可能就会太长了。

处理思路：采用流水线技术，以8点fft为例，我们使用三套蝶形运算电路，像流水线工场一样，每一级计算结果给到下一级在计算，这样最终达到的效果是原本计算一级的时间可以完成原来三级的运算。但同样也有一些缺点：如电路规模成倍数增加。

自己的一些思考：随着点数的增加，完全的流水线和完全不适用都是不好的，可以采用一些折中的方法。以1024点fft为例子：10级蝶形运算，我们可以使用5级流水，每一级流水完成两级蝶形运算，这样电路规模可以减小一些，且速度降低的不是很多。在具体的设计中，要根据实际设计要求选择合适的方法。
关于计算结果的思考：如果大家看来最终的仿真结果，会发现结果都是整数，这是因为使用的是整形存储方式，计算结果自然而然是整数。实际上在我认为在硬件电路中已经足够。硬件处理的信号大部分是由ADC采集的，以分辨率位12位的ADC为例，采集结果位0-4095之间任意数，也就是说一般ADC采集结果也是整形。
上述的问题和处理思路是自己在设计过程中思考，在某些方面可能说的很不到位。

2.电路结构

需要的模块：

复数加法，减法，乘法电路（都是单独设计的独立模块）。
乘法模块注意：因为是有符号数乘法，要注意符号，存储类型，以及是否会超出存储范围等问题。
两点蝶形运算模块：使用复数加法，减法，乘法等。（具体计算可以看之间文章公式）
使用两点的蝶形运算模块构成一级8点蝶形运算。
顶层模块：三级8点蝶形运算。

电路结构图：

两点蝶形运算模块

输入信号：两个输入值，以及旋转因子
输出信号：两个结果（一个蝶形运算两个值）
注意：都是复数
八点蝶形运算模块

输入信号：时钟信号，复位信号，8个输入信号，4个旋转因子
输出信号：8个蝶形运算结果
输出采用寄存器输出（时钟控制），构成流水线。
顶层模块

输入信号：时钟，复位，8个输入信号
输出信号：8个输出结果
旋转因子：在顶层模块提前设置好
上述使用的所以信号都是32位信号

3.仿真测试

`timescale 1 ps/ 1 ps
module fft_test_tb;

reg [31:0]i;

reg clk,rst;

reg			[31:0]		x0_real;
reg			[31:0]		x0_imag;
reg			[31:0]		x1_real;
reg			[31:0]		x1_imag;
reg			[31:0]		x2_real;
reg			[31:0]		x2_imag;
reg			[31:0]		x3_real;
reg			[31:0]		x3_imag;
reg			[31:0]		x4_real;
reg			[31:0]		x4_imag;
reg			[31:0]		x5_real;
reg			[31:0]		x5_imag;
reg			[31:0]		x6_real;
reg			[31:0]		x6_imag;
reg			[31:0]		x7_real;
reg			[31:0]		x7_imag;

wire 		[31:0]		fft_out0_real;
wire 		[31:0]		fft_out0_imag;
wire 		[31:0]		fft_out1_real;
wire 		[31:0]		fft_out1_imag;
wire 		[31:0]		fft_out2_real;
wire 		[31:0]		fft_out2_imag;
wire 		[31:0]		fft_out3_real;
wire 		[31:0]		fft_out3_imag;
wire 		[31:0]		fft_out4_real;
wire 		[31:0]		fft_out4_imag;
wire 		[31:0]		fft_out5_real;
wire 		[31:0]		fft_out5_imag;
wire 		[31:0]		fft_out6_real;
wire 		[31:0]		fft_out6_imag;
wire 		[31:0]		fft_out7_real;
wire 		[31:0]		fft_out7_imag;



fft_top fft_top_test(

	.clk				(clk),
	.rst				(rst),

	.x0_real			(x0_real),
	.x0_imag			(x0_imag),
	.x1_real			(x1_real),
	.x1_imag			(x1_imag),
	.x2_real			(x2_real),
	.x2_imag			(x2_imag),
	.x3_real			(x3_real),
	.x3_imag			(x3_imag),
	.x4_real			(x4_real),
	.x4_imag			(x4_imag),
	.x5_real			(x5_real),
	.x5_imag			(x5_imag),
	.x6_real			(x6_real),
	.x6_imag			(x6_imag),
	.x7_real			(x7_real),
	.x7_imag			(x7_imag),

	.fft_out0_real		(fft_out0_real),
	.fft_out0_imag		(fft_out0_imag),
	.fft_out1_real		(fft_out1_real),
	.fft_out1_imag		(fft_out1_imag),
	.fft_out2_real		(fft_out2_real),
	.fft_out2_imag		(fft_out2_imag),
	.fft_out3_real		(fft_out3_real),
	.fft_out3_imag		(fft_out3_imag),
	.fft_out4_real		(fft_out4_real),
	.fft_out4_imag		(fft_out4_imag),
	.fft_out5_real		(fft_out5_real),
	.fft_out5_imag		(fft_out5_imag),
	.fft_out6_real		(fft_out6_real),
	.fft_out6_imag		(fft_out6_imag),
	.fft_out7_real		(fft_out7_real),
	.fft_out7_imag		(fft_out7_imag)

);
	
initial clk=1;
always#10 clk=~clk;
	
initial begin
    rst=0;
	x0_real =  32'd0;
	x0_imag =  32'd0;
	x1_real =  32'd0;
	x1_imag =  32'd0;
	x2_real =  32'd0;
	x2_imag =  32'd0;
	x3_real =  32'd0;
	x3_imag =  32'd0;
	x4_real =  32'd0;
	x4_imag =  32'd0;
	x5_real =  32'd0;
	x5_imag =  32'd0;
	x6_real =  32'd0;
	x6_imag =  32'd0;
	x7_real =  32'd0;
	x7_imag =  32'd0;
	
    #201;
	rst=1;
	
	for(i=0;i<32'd400;i=i+1) begin
		@(posedge clk);
		x0_real =  x0_real +32'd1    ;
		x0_imag =  x0_imag +32'd2    ;
		x1_real =  x1_real +32'd1    ;
		x1_imag =  x1_imag +32'd5    ;
		x2_real =  x2_real +32'd31   ;
		x2_imag =  x2_imag +32'd3    ;
		x3_real =  x3_real +32'd1    ;
		x3_imag =  x3_imag +32'd6    ;
		x4_real =  x4_real +32'd23   ;
		x4_imag =  x4_imag +32'd41   ;
		x5_real =  x5_real +32'd8    ;
		x5_imag =  x5_imag +32'd6    ;
		x6_real =  x6_real +32'd11   ;
		x6_imag =  x6_imag +32'd1    ;
		x7_real =  x7_real +32'd1    ;
		x7_imag =  x7_imag +32'd7    ;


	end
	
	$stop;
end


endmodule

verilog实现fft,数字信号处理,算法,硬件工程,学习,傅立叶分析