Matlab的信号频谱分析——FFT变换
Matlab的信号频谱分析
FFT是离散傅立叶变换的快速算法,可以将一个时域信号变换到频域。
有些信号在时域上是很难看出什么特征的。但是如果变换到频域之后,就很容易看出特征了。
这就是很多信号分析采用FFT变换的原因。
另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
通俗点说FFT就是将一个信号解析成是由不同频率、幅值,相位的正弦波叠加而成的。
fft 函数出来的是个复数,每一个点分实部虚部两部分。假设采用1024点 fft,采样频率是 fs,那么第一个点对应 0 频率点,第512点对应的就是 fs/2 的频率点。然后从头开始找模值最大的那个点,其所对应的频率值应该就是你要的基波频率了。
【一个模拟信号,经过ADC采样之后,就变成了数字信号。根据采样定理,采样频率要大于信号频率的两倍。采样得到的数字信号,就可以做FFT变换了。N个采样点,经过FFT之后,就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方。】
fft 快速傅里叶变换
语法
Y = fft(X);
Y = fft(X,n);
Y = fft(X,n,dim);描述
Y = fft(X)用快速傅里叶转换FFT算法计算离散傅里叶变换DFT。
如果X是向量,那么fft(X)返回向量的傅里叶变换。
如果X是矩阵,那么fft(X)返回X中每一列向量的傅里叶变换。
Y = fft(X,n)指定进行n点DFT,如果X长度小于n则补零,如果X长度大于n则截断为n。
Y = fft(X,n,dim)根据维度进行傅里叶变换。FFT变换的步骤:
1、对模拟信号离散化
一个模拟信号,经过ADC采样之后,就变成了离散的数字信号。
2、采样频率(Fs)的选取
根据采样定理,采样频率需大于信号频率的两倍(一般取2.5~3)。
3、采样点数( N )的选取
在FFT变换中,输入N个采样点,就有N个变换结果,每个结果都是一个复数。
每个结果都和上面所说的一个正弦信号的频率、幅值,相位对应。
复数的幅值和正弦信号的幅值对应,相位和相位对应。
而其频率的对应关系为:假设第n个结果,则其对应的频率为 Fn = (n-1)*Fs/N 。
Fs/N为分辨率,例如采样频率Fs 为 1024Hz,采样点数为 1024点,
则每个结果以 1HZ 的频率步长递增。如果采样频率Fs 为 1024Hz,采样点数为 2048点,
则每个结果以 0.5HZ 的频率步长递增。我们讲其分辨率为 0.5HZ。
如果要提高频率分辨力,则必须增加采样点数,也即采样时间。
频率分辨率和采样时间是倒数关系。
注意:为了方便进行FFT运算,通常N取2的整数次方。
频率分辨率和采样时间是倒数关系。假设FFT之后某点 n 用复数 a+bi 表示,那么这个复数的模就是,相位就是。根据以上的结果,就可以计算出 n点(n≠1,且n<=N/2)对应的信号的表达式为:
,即
。对于 n=1 点的信号,是直流分量,幅度即为 A1/N。由于FFT结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
例:假设我们有一个信号,它含有一个2V的直流分量,一个频率为50Hz、相位为-30度、幅度为3V的交流信号,以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。
用数学表达式就是如下:
式中,cos 参数为弧度,所以-30度和90度要分别换算成弧度。
我们以256Hz的采样率对这个信号进行采样,总共采样256点。
按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第 n个点的频率就是 n-1。我们的信号有 3个频率:0Hz、50Hz、75Hz,应该分别在第 1个点、第 51个点、第 76个点上出现峰值,其它各点应该接近0。
实际情况如何呢?
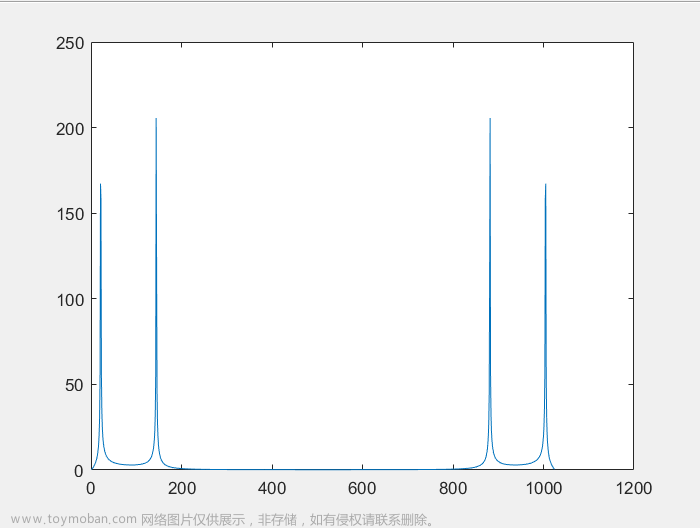
我们来看看FFT的结果的模值如下图所示:

很明显,1点、51点、76点的值都比较大,它附近的点值都很小,可以认为是 0,即在那些频率点上的信号幅度为 0。接着,我们来计算各点的幅度值。分别计算这三个点的模值,结果如下:
- 1点: 512
- 51点:384
- 76点:192
按照公式,可以计算出直流分量为:512/N = 512/256 = 2;50Hz信号的幅度为:384/(N/2) = 384/(256/2) = 3;75Hz信号的幅度为192/(N/2) = 192/(256/2) = 1.5。可见,从频谱分析出来的幅度是正确的。
Matlab 程序如下:
% 假设我们有一个信号,它含有一个2V的直流分量,一个频率为50Hz、相位为-30度、幅度为3V的交流信号,
% 以及一个频率为75Hz、相位为90度、幅度为1.5V的交流信号。
% 用数学表达式就是如下:S=2+3cos(2pi50t-pi30/180)+1.5cos(2pi75t+pi90/180)。
% 我们以256Hz的采样率对这个信号进行采样,总共采样256点。
% 按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,
% 第n个点的频率就是n-1。
% 我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第51个点、第76个点上出现峰值,
% 其它各点应该接近0。
% 实际情况如何呢?我们来看看FFT的结果:
clc; clear; close all;
% s1 = 2; % 一个2V的直流
% s2 = 3*cos(2*pi*50*t-pi*30/180); % 一个频率为50Hz、相位为-30度、幅度为3V的交流信号
% s3 = 1.5*cos(2*pi*75*t+pi*90/180); % 一个频率为75Hz、相位为90度、幅度为1.5V的交流信号
% y = 2 + 3*cos(2*pi*50*t-pi*30/180) + 1.5*cos(2*pi*75*t+pi*90/180); % 信号叠加
Adc = 2; %直流分量幅度
A1 = 3; %频率F1信号的幅度
A2 = 1.5; %频率F2信号的幅度
F1 = 50; %信号1频率(Hz)
F2 = 75; %信号2频率(Hz)
Fs = 256; %采样频率(Hz)
P1 = -30; %信号1相位(度)
P2 = 90; %信号相位(度)
N = 256; %采样点数
t = (0:N-1)/Fs; %采样时刻
%信号
S = Adc + A1*cos(2*pi*F1*t+pi*P1/180) + A2*cos(2*pi*F2*t+pi*P2/180);
%显示原始信号
figure('Name','原始时域信号');
plot(t, S);
xlabel('时间/s'); ylabel('幅值/v');
title('时域信号time domain signal');
figure('Name','FFT 模值');
Y = fft(S, N); %做FFT变换
Ayy = (abs(Y)); %取模
plot(Ayy(1:N)); %显示原始的FFT模值结果
ylabel('幅度/v');
title('FFT 模值');
figure('Name','幅度-频率曲线图');
Ayy = Ayy/(N/2); %换算成实际的幅度
Ayy(1) = Ayy(1)/2;
df = Fs/N; %频率分辨率
F = (0:(N-1))*Fs/N; %换算成实际的频率值 %即每点的频率,第一个点对应的频率为0.
plot(F(1:N/2), Ayy(1:N/2)); %显示换算后的FFT模值结果
%由于傅里叶算法转换得到的是对称图,而常用的只需要一半就可以了.
xlabel('频率/Hz'); ylabel('幅度/v');
title('幅度-频率曲线图');
figure('Name','相位-频率曲线图');
Pyy = 1:N/2;
for i = 1:N/2
Pyy(i) = phase(Y(i)); %计算相位
Pyy(i) = Pyy(i)*180/pi; %换算为角度°
end
plot(F(1:N/2), Pyy(1:N/2)); %显示相位图
xlabel('频率/Hz'); ylabel('相位/°');
title('相位-频率曲线图');
%
%
% FFT结果的幅值和信号真实幅值对应的关系:除第一个点外,
% FFT结果的其他点的幅值是真实信号幅值N/2倍,而第一个点是真实值的N倍。
%
% FFT结果的相位和真实信号相位对比:由于是第51个点对应的是50Hz,有个错位关系,
% 还有就是FFT的幅值和真实值也有个转换关系,下面我们通过算法让其完全对应起来。
%
%




总结
总结:假设采样频率为Fs,采样点数为N,做N点FFT之后,某一点n(n从1开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以 N/2 就是对应该频率下的信号的幅度(对于直流信号是除以N);该点的相位即是对应该频率下的信号的相位。相位的计算可用函数 atan2(b,a) 计算。atan2(b,a) 是求坐标为(a,b)点的角度值,范围从 -pi 到 pi 。要精确到 xHz,则需要采样长度为1/x秒的信号,并做FFT。要提高频率分辨率,就需要增加采样点数,这在一些实际的应用中是不现实的,需要在较短的时间内完成分析。解决这个问题的方法有频率细分法,比较简单的方法是采样比较短时间的信号,然后在后面补充一定数量的0,使其长度达到需要的点数,再做FFT,这在一定程度上能够提高频率分辨力。
实例:
例:某信号由3个正弦信号组成,频率分辨率分别为1Hz、2.5Hz、3Hz,采样频率为10Hz。分别以N=20、40、128来分析该信号。
clc; clear; close all;
M = 256; %数据长度
fs = 10; %采样频率
f1 = 1; f2 = 2.5; f3 = 3; % 3个正弦信号的频率
t = (0:M-1)/fs; %设置时间序列
x = sin(2*pi*f1*t) + sin(2*pi*f2*t) + sin(2*pi*f3*t); %信号波形
N1 = 20; % N点FFT
N2 = 40;
N3 = 128;
X1 = fft(x,N1); %进行FFT 变换
X2 = fft(x,N2);
X3 = fft(x,N3);
freq1 = (0:N1/2)*fs/N1; %计算3个信号的频率刻度
freq2 = (0:N2/2)*fs/N2;
freq3 = (0:N3/2)*fs/N3;
plot(freq1, abs(X1(1:N1/2+1)), 'k:','color',[.8 0 0],'LineWidth',1); %作图
hold on;
plot(freq2, abs(X2(1:N2/2+1)), 'k-','color',[0 0.7 0],'LineWidth',1);
plot(freq3, abs(X3(1:N3/2+1)), 'k-','color',[.6 .6 0],'LineWidth',1);
legend('N=20','N=40','N=128');
title('不同N值得 DFT变换');
xlabel('频率/Hz'); ylabel('幅值');
set(gcf,'color','w');
set(gca,'Fontname','Monospaced');

从图中可以看出,
当N=20点时,虽然2.5Hz和3Hz这两个峰值大致能分开,但还是不太明显,可以认为是两个峰值,也可能被误认为有一个峰值在这两点之间。
当N=40时这两个峰值十分明显了,因为N增加一倍后在这两点之间增加了一个谷值,从而突出了峰值。文章来源:https://www.toymoban.com/news/detail-628623.html
而当N=128时峰值更明显了,但是由于栅栏现象和矩形窗泄露存在,3个正弦信号虽然输入幅值相同,但从频域上反映出的幅值各不相同。文章来源地址https://www.toymoban.com/news/detail-628623.html
到了这里,关于Matlab的信号频谱分析——FFT变换的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!