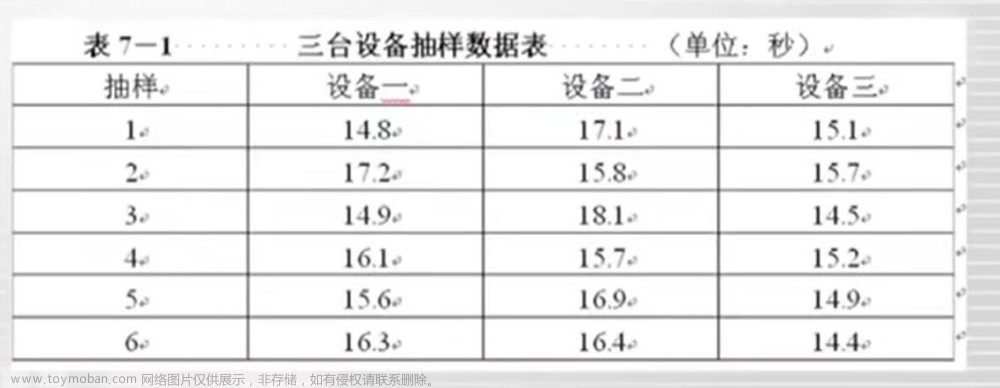
一、似然
在统计学中,似然性(likelihood)”和“概率”有明确的区分:
概率,用于在已知一些参数的情况下,预测接下来在观测上所得到的结果;
似然性,则是用于在已知某些观测所得到的结果时,对有关事物之性质的参数进行估值。
以高斯分布为例,其可以用参数μ和σ来描述。采样和参数估计是互逆的过程,从分布中采样是已知一些参数,得到观测结果,结果出现的可能性就用“概率”来表示。而在已知猜测结果时,对分布的参数进行估计和猜测,参数估计的可能性就用“似然"来表示。

文章来源地址https://www.toymoban.com/news/detail-628914.html
二、极大似然估计(Maximum Likelihood Estimation, MLE)
在统计学中,最大似然估计(maximum likelihood estimation,MLE),也称极大似然估计,是用来估计一个概率模型的参数的一种方法。最大似然估计在统计学和机器学习中具有重要的价值,常用于根据观测数据推断最可能的模型参数值。
还是以高斯分布为例。我们现在有一组采样数据,我么想要知道它是来自哪一个高斯分布(即估计高斯分布的参数μ和σ),这就可以用MLE来算。

每一个数据被采样的概率都可以写成一个条件概率的形式,表示从参数μ和σ的高斯分布中被采样的可能性大小。由于他们是独立同分布的,所以同时出现的概率(联合概率)体现为概率的连乘。这个连乘最大时所取的μ和σ,就是我们要找的那个高斯分布。


连乘容易引起下溢出,可以用ln来处理。

补充:
1. 最小二乘估计只是极大似然估计在高斯分布下的一种特殊形式(可以数学推导得到)。
参考:
https://www.bilibili.com/video/BV1QM4y167oZ/?spm_id_from=333.337.search-card.all.click&vd_source=2758ef806213f133641bb5da6406140b
周志华《西瓜书》7.2 节文章来源:https://www.toymoban.com/news/detail-628914.html
到了这里,关于似然与极大似然估计的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!