P1833 樱花（多重背包）（内附封面）-Toy模板网

这篇具有很好参考价值的文章主要介绍了P1833 樱花（多重背包）（内附封面）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

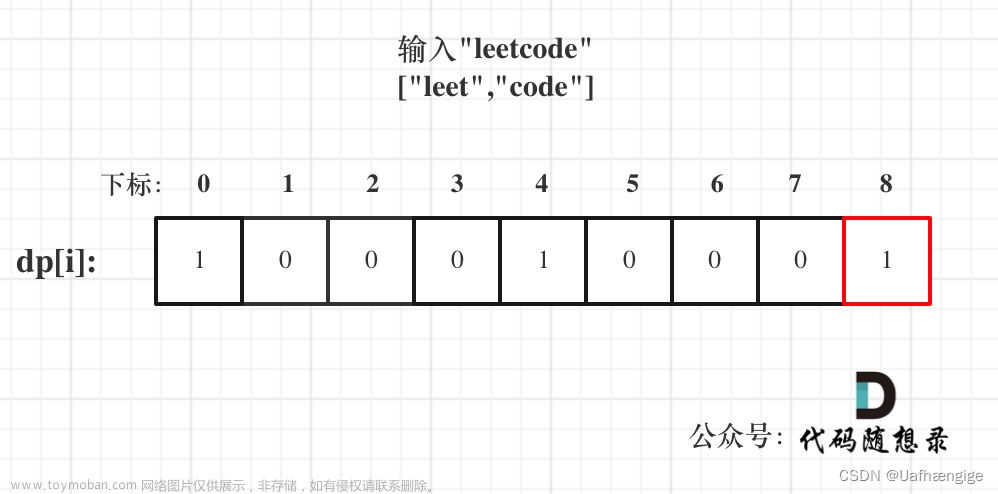
樱花

题目背景

《爱与愁的故事第四弹·plant》第一章。

题目描述

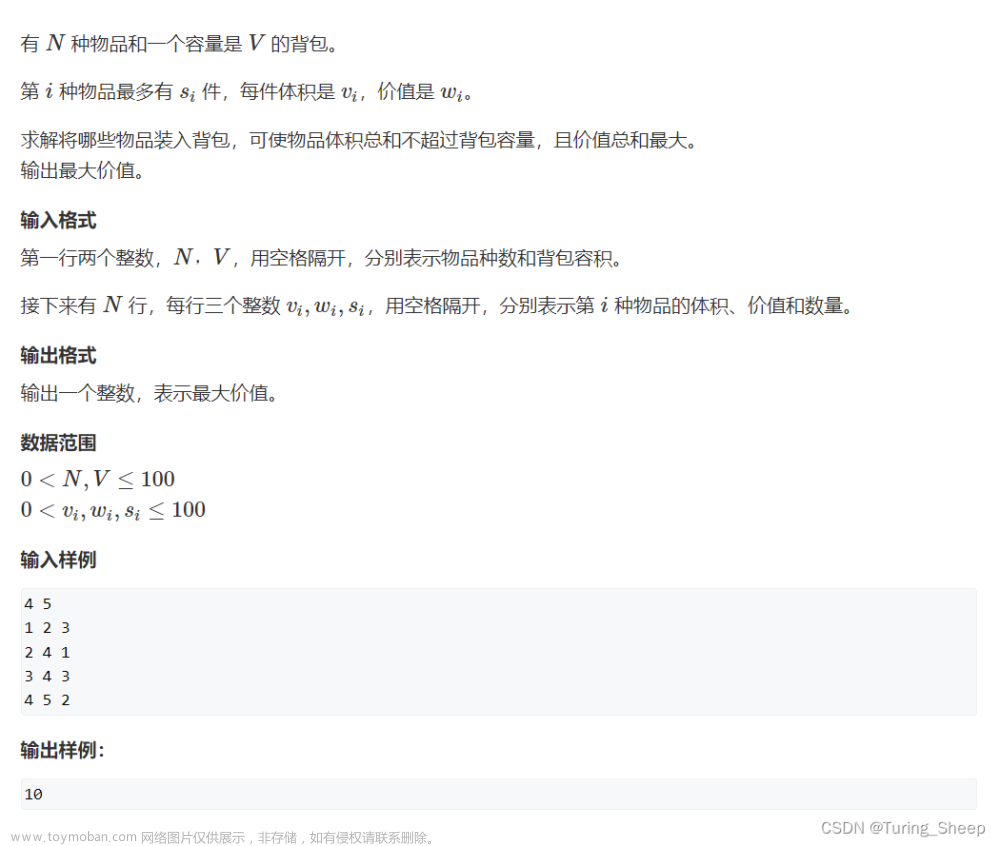
爱与愁大神后院里种了 $n$ 棵樱花树，每棵都有美学值 $C_i(0 \le C_i \le 200)$ 。爱与愁大神在每天上学前都会来赏花。爱与愁大神可是生物学霸，他懂得如何欣赏樱花：一种樱花树看一遍过，一种樱花树最多看 $P_i(0 \le P_i \le 100)$ 遍，一种樱花树可以看无数遍。但是看每棵樱花树都有一定的时间 $T_i(0 \le T_i \le 100)$ 。爱与愁大神离去上学的时间只剩下一小会儿了。求解看哪几棵樱花树能使美学值最高且爱与愁大神能准时（或提早）去上学。

输入格式

共 $n + 1$ 行：

第 $1$ 行：现在时间 $T_s$ （几时：几分），去上学的时间 $T_e$ （几时：几分），爱与愁大神院子里有几棵樱花树 $n$ 。这里的 $T_s$ ， $T_e$ 格式为：hh:mm，其中 $\leq hh \leq 23$ ， $\leq mm \leq 59$ ，且 $hh, mm, n$ 均为正整数。

第 $2$ 行到第 $n + 1$ 行，每行三个正整数：看完第 $i$ 棵树的耗费时间 $T_i$ ，第 $i$ 棵树的美学值 $C_i$ ，看第 $i$ 棵树的次数 $P_i$ （ $P_i=0$ 表示无数次， $P_i$ 是其他数字表示最多可看的次数 $P_i$ ）。

输出格式

只有一个整数，表示最大美学值。

样例 #1

样例输入 #1

6:50 7:00 3
2 1 0
3 3 1
4 5 4

样例输出 #1

提示

$100\%$ 数据： $T_e-T_s \leq 1000$ （即开始时间距离结束时间不超过 $1000$ 分钟）， $\leq 10000$ 。保证 $T_e,T_s$ 为同一天内的时间。

样例解释：赏第一棵樱花树一次，赏第三棵樱花树 $2$ 次。

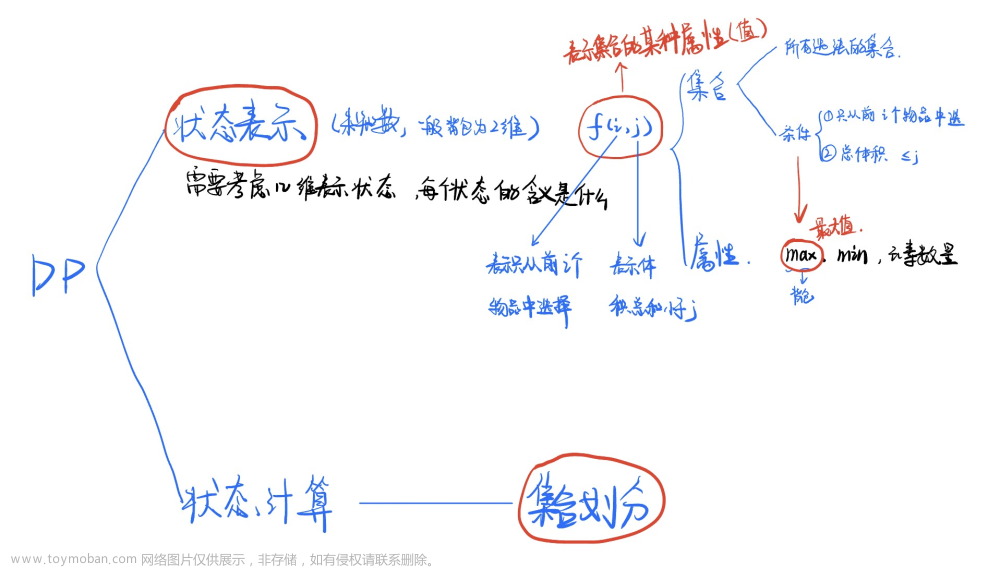
大致思路

二进制拆分
做法：把每一个物品根据2的多少次方拆分，因为任何数都可以转化为二进制数

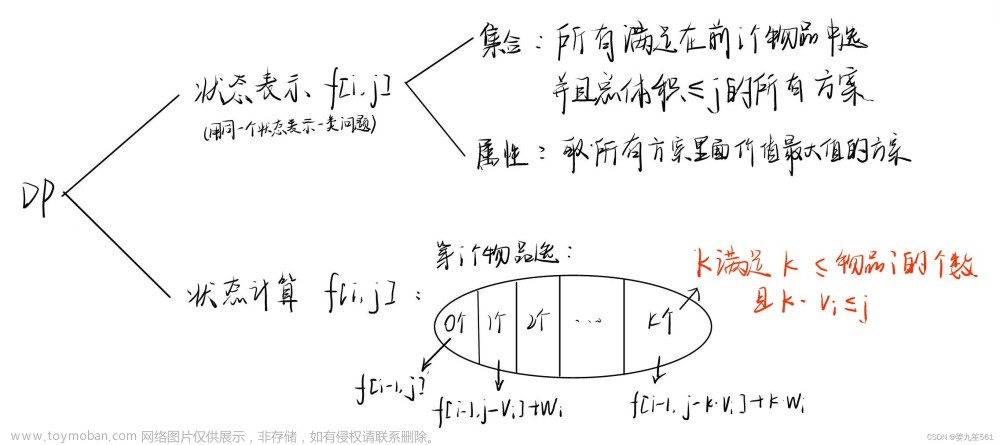
核心思想 ：把每一个物品拆成很多个，分别计算价值和所需时间，再转化为01背包求解

最后一点 ：完全背包可以把他的空间记为999999，不要太大，一般百万就足够了，当然也可以分开做背包

$f [j] = ma x (f [j], f [j - w [i]] + v [i])$

#include<bits/stdc++.h>
using namespace std;
#define int long long int 
#define intt int
const int N=1e5;
int n,zw,M;
int a[N*11],w[N*11],v[N*11],f[110050];
signed main(){
	char l;
	int h1,m1,h2,m2;
	cin>>h1>>l>>m1;
	cin>>h2>>l>>m2;
	zw=h2*60+m2-h1*60-m1;
	cin>>n;
	M=1;
	for(int i=1;i<=n;i++){
		int ww,vv,pp;
		cin>>ww>>vv>>pp;
		if(pp==1){
			w[M]=ww;
			v[M]=vv;
			M++;
		}
		else {
			if(pp==0)pp=zw;
			int tmp=1;
			while(pp){
				w[M]=tmp*ww;
				v[M]=tmp*vv;
				M++;
				pp-=tmp;
				tmp*=2;
				if(pp<tmp){
					w[M]=pp*ww;
					v[M]=pp*vv;
					M++;
					break;
				}
			}
		}
	}
	for(int i=1;i<=M;i++){
		for(int j=zw;j>=w[i];j--){
			f[j]=max(f[j],f[j-w[i]]+v[i]);
		} 
	}
	cout<<f[zw];
	return 0;
}