目录
1、递归
2、二分查找
3、排序算法
分类
3.1、冒泡排序
3.2、选择排序
3.3、插入排序
3.4、希尔排序(高级插入排序)
3.5、归并排序
3.6、快速排序
核心思想
具体步骤
代码实现
3.7、堆排序
3.8、计数排序
3.9、桶排序
3.10、基数排序
4、字符串匹配算法
4.1、BF算法
4.2、RK算法
4.3、BM算法
4.3.1、一个例子理解一下
4.3.2、原理
4.3.2.1、坏字符规则
4.3.2.2、好后缀规则
4.4、Trie树
4.4.1、插入
4.4.2、查找
4.4.3、实现
5、算法思维
5.1、贪心算法
5.1.1、概念
5.1.2、部分背包问题
5.2、分治算法
5.3、回溯算法
5.4、动态规划
5.4.1、斐波那契数列:
1)递归分治+记忆搜索(备忘录)
2)递推(dp方程)
1、递归
- 概念:在函数的定义中调用函数自身的方法。或者说,递归算法是一种直接或者间接调用自身函数/方法的算法。
- 本质:是一种循环,在循环中调用自己。需要设置结束条件,避免函数无限递归导致OOM。
- 优缺点:递归可以使代码变得更简洁,但如果递归太深,可能造成栈溢出。如果退出条件设置不合理,也很有可能造成OOM。
- 应用:二分查找、快速排序、归并排序、树的遍历、回溯算法、分治算法、动态规划等。
- 经典案例:斐波那契数列,普通递归时间复杂度为O(2^n)。以下方式会有大量重复计算,可利用动态规划进行优化。
<!--斐波那契数列:0、1、1、2、3、5、8、13、21、34、55.....
规律:从第3个数开始,每个数等于前面两个数的和
递归分析:
函数的功能:返回n的前两个数的和
递归结束条件:从第三个数开始,n<=2
函数的等价关系式:fun(n)=fun(n-1)+fun(n-2)
-->
//递归实现
public static int fun2(int n) {
if (n <= 1) return n;
return fun2(n - 1) + fun2(n - 2);
}
public static void main(String[] args) {
fun1(9);
System.out.println("==================================");
System.out.println(fun2(9));
}2、二分查找
- 概念:也叫做折半查找法。是针对有序数据集合的查找算法,不适用于无序数据集合。
- 本质:查找时,每次与数据集合中间的数mid进行匹配。匹配成功则直接返回,如果大于mid,则舍弃小于mid那一半;如果小于mid,则舍弃大于mid那一半。这样,每一次比较都能排除掉一半的元素,收缩快。
- 时间复杂度:O(logn)。
- 优缺点:速度快,不占额外空间,但二分查找只能针对有序数据。数据量太小意义不大,但数据量太大会占用连续的空间,也不太合适。
- 应用:所有有序数据集合的查找。
- while循环实现
/**
* 在有序数组中找到某个数的位置
*/
public static int binarySearch(int[] nums, int t) {
int low = 0; //低位索引
int high = nums.length - 1; //高位索引
int mid = 0; //中间索引
while (low <= high) {
mid = (low + high) / 2;
if (t == nums[mid]){ //等于半数
return mid;
} else if(t < nums[mid]){ //半数以里
high=mid-1;
} else {
low=mid+1; //半数以外
}
}
return -1;
}- 递归实现
/**
* 二分查找
*title:recursionBinarySearch
*@param arr 有序数组
*@param key 待查找关键字
*@return 找到的位置
*/
public static int recursionBinarySearch(int[] arr,int key,int low,int high){
if(key < arr[low] || key > arr[high] || low > high){
return -1;
}
int middle = (low + high) / 2; //初始中间位置
if(arr[middle] > key){
//比关键字大则关键字在左区域
return recursionBinarySearch(arr, key, low, middle - 1);
}else if(arr[middle] < key){
//比关键字小则关键字在右区域
return recursionBinarySearch(arr, key, middle + 1, high);
}else {
return middle;
}
}3、排序算法
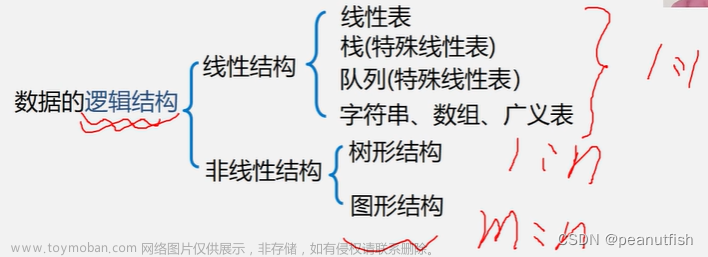
分类
时间复杂度为O(n²):冒泡排序、选择排序、插入排序、希尔排序
时间复杂度为O(nlogn):快速排序、归并排序、堆排序
时间复杂度为线性:计数排序(O(m+n))、桶排序(O(n))、基数排序
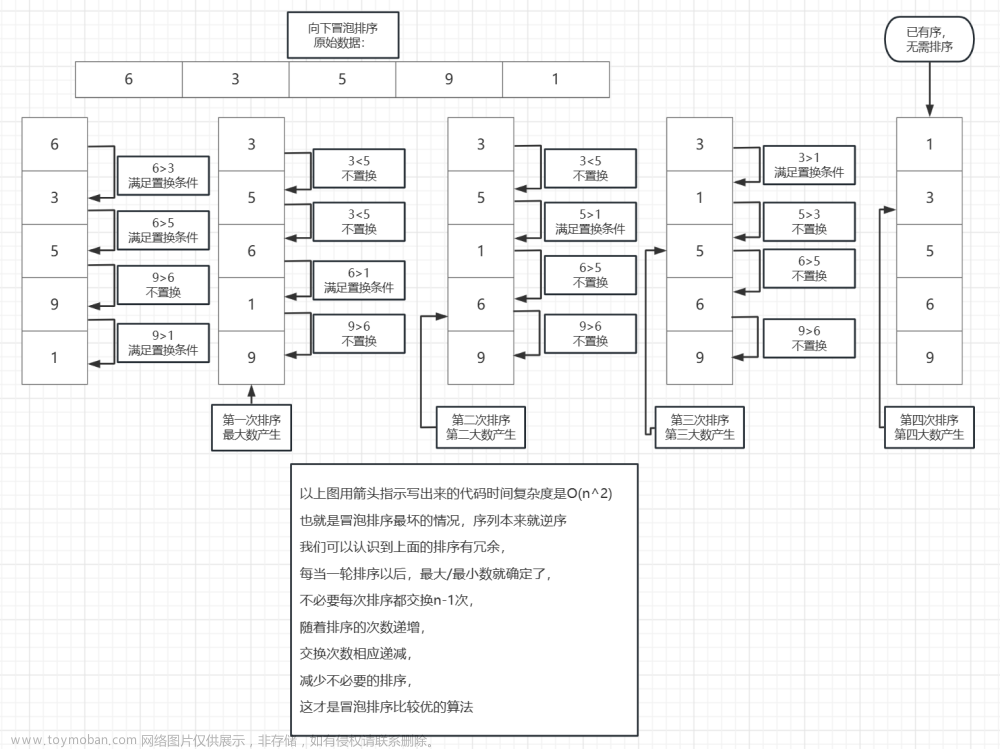
3.1、冒泡排序
依次比较相邻的元素,如果不符合排序条件则交换两个元素。这样每一轮比较后,最大(小)的值都会移动到数组尾部。N-1轮过后,排序完成。
public static int[] bubbleSort(int[] arr) {
int length = arr.length;
for (int i=0;i<length-1;i++) {
for (int j=0;j<length-1-i;j++) {
if (arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
}3.2、选择排序
每一轮都从未排序序列中找到最大(小)元素,存放到已排序序列的末尾。经过n-1轮过后,排序完成。

public static int[] selectionSort(int[] arr) {
int length = arr.length;
int min;
for (int i=0;i<length-1;i++) {
min = i;
for (int j=i+1;j<length;j++) {
if (arr[min] > arr[j]) {
min = j;
}
}
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
return arr;
}3.3、插入排序
构建一个有序序列,将未排序的数据,一个一个地插入到有序序列中。

public static int[] insertSort(int[] arr) {
for (int i=0;i<arr.length;i++) {
int temp = arr[i]; //要插入的数据
int j=i;
// 从已经排序的序列最右边的开始比较,找到比其小的数
while (j>0 && arr[j-1] > temp) {
arr[j] = arr[j-1];
j--;
}
if (j != i) { // 存在比其小的数,插入
arr[j] = temp;
}
}
return arr;
}3.4、希尔排序(高级插入排序)
核心:插入排序 + 分组。
首次增量 = length/2,之后每一次循环,分组step = step/2。
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
举例说明:
现有数组[12, 23, 25, 5, 32, 10, 13, 23, 27, 38],长度为10。
1、首次排序增量step = 5,将数组分为[12, 10],[23, 13],[25, 23], [5, 27], [32, 38]。
分别对三个数组进行插入排序,得到[10, 12], [13, 23], [23, 25], [5, 27], [32, 38]五个有序小数组,即[10, 13, 23, 5, 32, 12, 23, 25, 27, 38]。
2、第二次排序增量为step = 5/2 = 2, 将数组分为[10, 23, 32, 23, 27]和[13, 5, 12, 25, 38]。
分别对两个数组进行插入排序,得到[10, 23, 23 ,27, 32]和[5, 12, 13, 25, 38]两个有序小数组,即[10, 5, 23, 12, 23, 13, 27, 25, 32, 38],达到宏观有序。
3、第三次排序增量为step = 2/2 =1,直接对上一步数组进行插入排序。
得到[5, 10, 12, 13, 23, 23, 25, 27, 32, 38]。完成排序。
public static int[] shellSort(int[] arr) {
int length = arr.length;
// step: 增量, 每次都/2
for (int step = length / 2; step >= 1; step /= 2) {
// 从增量那组开始进行插入排序,直至完毕
for (int i = step; i < length; i++) {
int j = i;
int temp = arr[j];
// j - step 就是代表与它同组隔壁的元素
while (j - step >= 0 && arr[j - step] > temp) {
arr[j] = arr[j - step];
j = j - step;
}
arr[j] = temp;
}
}
return arr;
}3.5、归并排序
分治思想,将大问题拆解为小问题,递归将大数组拆分成小数组(只有一个元素的数组),分别对小数组进行排序,然后再合并小数组。

public int[] sort(int[] a, int low, int high) {
int mid = (low + high) / 2;
if (low < high) {
sort(a, low, mid);
sort(a, mid+1, high);
merge(a, low, mid, high);
}
return a;
}
public void merge(int[] a, int low, int mid, int high) {
int[] temp = new int[high - low + 1];
int i = low;
int j = mid + 1;
int k = 0;
while (i <= mid && j <= high) {
if (a[i] < a[j]) {
temp[k++] = a[i++];
} else {
temp[k++] = a[j++];
}
}
while (i <= mid) {
temp[k++] = a[i++];
}
while (j <= high) {
temp[k++] = a[j++];
}
for (int x = 0; x < temp.length; x++) {
a[x + low] = temp[x];
}
}3.6、快速排序
核心思想
设置两个变量low和high,排序开始时,low = 0, high = size-1;
从数组中找一个基准值,所有元素比基准值小的摆放在基准值前,所有元素比基准值大的摆放在基准值后。
具体步骤
1、从数列中挑出一个元素,称为 “基准元素”;
2、重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区操作;
3、递归地把小于基准值元素的子数列和大于基准值元素的子数列分别进行快速排序。
代码实现
private void swap(int[] arr, int x, int y) {
int temp = arr[x];
arr[x] = arr[y];
arr[y] = temp;
}
private void quick_sort_recursive(int[] arr, int start, int end) {
if (start >= end)
return;
int mid = arr[end];
int left = start, right = end - 1;
while (left < right) {
while (arr[left] <= mid && left < right)
left++;
while (arr[right] >= mid && left < right)
right--;
swap(arr, left, right);
}
if (arr[left] >= arr[end])
swap(arr, left, end);
else
left++;
quick_sort_recursive(arr, start, left - 1);
quick_sort_recursive(arr, left + 1, end);
}3.7、堆排序


将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。 将其与末尾元素进行交换,此时末尾就为最大值。
然后将剩余n-1个元素重新构造成一个堆,这样会得 到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
public static void sort(int[] array) {
// 1. 把无序数组构建成最大堆
// array.lentgh /2 - 1 : 第一个非叶子节点的左孩子
for (int i = array.length / 2 - 1; i >= 0; i--) {
adjustHeap(array, i, array.length);
}
// 2. 调整堆结构+交换堆顶元素与末尾元素,调整堆产生新的堆顶
for (int i = array.length - 1; i > 0; i--) {
// 最后1个元素和第1个元素进行交换
int temp = array[i];
array[i] = array[0];
array[0] = temp;
// “下沉”调整最大堆
adjustHeap(array, 0, i);
}
}
public static void adjustHeap(int []array,int parentIndex,int length){
// temp 保存父节点值,用于最后的赋值
int temp = array[parentIndex];
int childIndex = 2 * parentIndex + 1;
while (childIndex < length){
// 如果有右孩子,且右孩子大于左孩子的值,则定位到右孩子
if (childIndex + 1 < length && array[childIndex + 1] >
array[childIndex]){
childIndex++;
}
// 如果父节点大于任何一个孩子的值,则直接跳出
if (temp >= array[childIndex])
break;
//无须真正交换,单向赋值即可
array[parentIndex] = array[childIndex];
parentIndex = childIndex;
//下一个左孩子
childIndex = 2 * childIndex + 1;
}
array[parentIndex] = temp;
}3.8、计数排序
使用一个额外的数组进行排序记录,其中第i个元素就是待排序数组A中值等于i的元素的个数。
适合于连续的取值范围不大的数组。
不连续和取值范围过大会造成数组过大。
比如:待排序元素集合为:9,1,2,7,8,1,3,6,5,3。排序如下所示:

public static int[] countSort(int[] array, int offset) {
int[] nums = new int[array.length];
for (int i = 0; i < array.length; i++) {
int n = (array[i] - offset);
//数字自增
nums[n]++;
}
int[] nums2 = new int[array.length];
// i是计数数组下标,k是新数组下标
for (int i = 0, k = 0; i < nums.length; i++) {
for (int j = 0; j < nums[i]; j++) {
nums2[k++] = i + offset;
}
}
return nums2;
}3.9、桶排序
分治思想,将待排序数组元素,分到有限数量的桶里。每个桶再进行单独排序,最后按顺序将各个桶中的元素输出。
每一个桶(bucket)代表一个区间范围,里面可以承载一个或多个元素。
每个桶的区间跨度 = (最大值-最小值)/ (桶的数量 - 1)。
比如,有数组[4.5、0.84、3.25、2.18、0.5],设置桶的数量为5,则可分为以下几个桶

public static double[] bucketSort(double[] array) {
double max = 0;
double min = 0;
//获得最大值和最小值之间的差
for (int i = 0; i < array.length; i++) {
if (array[i] > max) {
max = array[i];
}
if (array[i] < min) {
min = array[i];
}
}
double d = max - min;
//桶初始化
int bucketNum = array.length;
ArrayList<LinkedList<Double>> bucketList =
new ArrayList<LinkedList<Double>>(bucketNum);
for (int i = 0; i < bucketNum; i++) {
bucketList.add(new LinkedList<Double>());
}
//将每个元素放入桶中
for (int i = 0; i < array.length; i++) {
int num = (int) ((array[i] - min) * (bucketNum - 1) / d);
bucketList.get(num).add(array[i]);
}
//对每个桶内部进行排序
for (int i = 0; i < bucketList.size(); i++) {
Collections.sort(bucketList.get(i));
}
//输出全部元素
double[] sortedArray = new double[array.length];
int index = 0;
for (LinkedList<Double> list : bucketList) {
for (double element : list) {
sortedArray[index] = element;
index++;
}
}
return sortedArray;
}3.10、基数排序
假设有待排序数组[53, 3, 542, 748, 14, 214, 154, 63, 616],排序图解如下:
 将整数按位数切割,然后对每个位数分别比较(依次比较个位、十位、百位、千位......)。比较方式有两种,为LSD和MSD。
将整数按位数切割,然后对每个位数分别比较(依次比较个位、十位、百位、千位......)。比较方式有两种,为LSD和MSD。
- MSD:先从高位开始进行排序,在每个关键字上,可采用计数排序。
- LSD:先从低位开始进行排序,在每个关键字上,可采用桶排序。
public static void lsd_RadixSort(int[] arr,int max) {
//bucket用来当桶,放数据,取数据
int[] bucket = new int[arr.length];
//k表示第几位,1代表个位,2代表十位,3代表百位...
for(int k=1;k<=max;k++) {
int[] count = new int[arr.length];
//分别统计第k位是0,1,2,3,4,5,6,7,8,9的数量
//即此循环用来统计每个桶中的数据的数量
for(int i=0;i<arr.length;i++) {
count[getFigure(arr[i],k)]++;
}
//利用count[i]来确定放置数据的位置
for(int i=1;i<arr.length;i++) {
count[i] = count[i] + count[i-1];
}
//执行完此循环之后的count[i]就是第i个桶右边界的位置
//利用循环把数据装入各个桶中,注意是从后往前装
for(int i=arr.length-1;i>=0;i--) {
int j = getFigure(arr[i],k);
bucket[count[j]-1] = arr[i];
count[j]--;
}
//将桶中的数据取出来,赋值给arr
for(int i=0,j=0;i<arr.length;i++,j++) {
arr[i] = bucket[j];
}
}
}
//此函数返回整型数i的第k位是什么
public static int getFigure(int i,int k) {
int[] a = {1,10,100};
return (i/a[k-1])%10;
}4、字符串匹配算法
从一个字符串中,判断是否包含一个子串。(indexOf()函数)。
4.1、BF算法
Brute Force,暴力匹配算法。在字符串 A 中查找字符串 B,那字符串 A 就是主串,字符串 B 就是子串。在主串中,检查起始位置分别是 0、1、2…n-m 且长度为 m 的 n-m+1 个子串,看有没有跟子串匹配的字符串。
时间复杂度为O(m*n),m为子串长度,n为主串长度。
public boolean isMatch(String str, String sub) {
for (int i = 0; i <= str.length() - sub.length(); i++) {
for (int j = 0; j < sub.length(); j++) {
if (str.charAt(i+j) != sub.charAt(j)) {
break;
}
if (j == sub.length() - 1) {
return true;
}
}
}
return false;
}4.2、RK算法
Rabin-Karp算法,通过哈希算法对主串中的 n-m+1 个子串分别求哈希值,然后逐个与子
串的哈希值比较大小。如果有任意一个哈希值与子串的哈希值相等,则说明匹配成功。
public static boolean isMatch(String main, String sub) {
//算出子串的hash值
int hash_sub = strToHash(sub);
for (int i = 0; i <= (main.length() - sub.length()); i++) {
// 主串截串后与子串的hash值比较
if (hash_sub == strToHash(main.substring(i, i + sub.length()))) {
return true;
}
}
return false;
}
/**
* 支持 a-z 二十六进制
* 获得字符串的hash值
* 比如:字符串abc,a的ascii=97,b的ascii=98,c的ascii=99。
* 那么,字符串abc的hash值 = 97 * 26² + 98 * 26¹ + 99 * 26º = 68219
* @param src
* @return
*/
public static int strToHash(String src) {
int hash = 0;
for (int i = 0; i < src.length(); i++) {
hash += src.charAt(i) * Math.pow(26, src.length() - i -1);
}
return hash;
}4.3、BM算法
Boyer-Moore算法,滑动算法。减少比较次数,避免一些肯定不会匹配字符串的比较。
时间复杂度为O(n/m)。
4.3.1、一个例子理解一下

4.3.2、原理
当不匹配的时候 一次性可以跳过不止一个字符 。即它不需要对被搜索的字符串中的字符进行逐一比较,而会跳过其中某些部分。
4.3.2.1、坏字符规则
字符串匹配失败时,移动的位数 = 坏字符在子串中的位置si - 坏字符在子串中最右出现的位置xi。
如果坏字符没有在子串中出现,那么xi = -1。



private static final int SIZE = 256; // 全局变量或成员变量
/**
*
* @param b
* @param m
* @param dc
*/
private static void generateBC(char[] b, int m, int[] dc) {
for (int i = 0; i < SIZE; ++i) {
dc[i] = -1; // 初始化 bc 模式串中没有的字符值都是-1
}
//将模式串中的字符希写入到字典中
for (int i = 0; i < m; ++i) {
int ascii = (int)b[i]; // 计算 b[i] 的 ASCII 值
dc[ascii] = i;
}
}
/**
* 坏字符
* @param a 主串
* @param b 模式串
* @return
*/
public static int bad(char[] a, char[] b) {
//主串长度
int n=a.length;
//模式串长度
int m=b.length;
//创建字典
int[] bc = new int[SIZE];
// 构建坏字符哈希表,记录模式串中每个字符最后出现的位置
generateBC(b, m, bc);
// i表示主串与模式串对齐的第一个字符
int i = 0;
while (i <= n - m) {
int j;
for (j = m - 1; j >= 0; --j) { // 模式串从后往前匹配
//i+j : 不匹配的位置
if (a[i+j] != b[j]) break; // 坏字符对应模式串中的下标是j
}
if (j < 0) {
return i; // 匹配成功,返回主串与模式串第一个匹配的字符的位置
}
// 这里等同于将模式串往后滑动j-bc[(int)a[i+j]]位
// j:si bc[(int)a[i+j]]:xi
i = i + (j - bc[(int)a[i+j]]);
}
return -1;
}4.3.2.2、好后缀规则
字符串匹配失败时,后移位数 = 好后缀在子串中的位置 - 好后缀在子串上一次出现的位置,且如果好后缀在子串中没有再次出现,则为 -1。

4.4、Trie树
也叫字典树,树形结构,专门处理字符串匹配的数据结构,用来解决在一组字符串中快速查找某个字符串的问题。
本质就是利用字符串的公共前缀,将重复的前缀合并在一起。
根节点不包含任何信息,从根节点到叶子结点的一条路径,构成一个字符串。

4.4.1、插入


4.4.2、查找
4.4.3、实现

public class TrieNode {
public char data;
public TrieNode[] children = new TrieNode[26];
public boolean isEndingChar = false;
public TrieNode(char data) {
this.data = data;
}
}
public class Trie {
private TrieNode root = new TrieNode('/'); // 存储无意义字符
// 往Trie树中插入一个字符串
public void insert(char[] text) {
TrieNode p = root;
for (int i = 0; i < text.length; ++i) {
int index = text[i] - 97;
if (p.children[index] == null) {
TrieNode newNode = new TrieNode(text[i]);
p.children[index] = newNode;
}
p = p.children[index];
}
p.isEndingChar = true;
}
// 在Trie树中查找一个字符串
public boolean find(char[] pattern) {
TrieNode p = root;
for (int i = 0; i < pattern.length; ++i) {
int index = pattern[i] - 97;
if (p.children[index] == null) {
return false; // 不存在pattern
}
p = p.children[index];
}
if (p.isEndingChar == false) return false; // 不能完全匹配,只是前缀
else return true; // 找到pattern
}
}5、算法思维
5.1、贪心算法
5.1.1、概念
一种在每一个步骤中都采取在当前状态下最好或最后的选择,从而希望导致结果是全局最好或最优的算法。(在当前选择做最优选择,不能回退)。
在不考虑排序的前提下,贪心算法只需要依次循环,所以时间复杂度为O(n)。
性能高,能用贪心算法解决的往往是最优解;但实际场景下应用不多。


5.1.2、部分背包问题
- 背包问题:背包有最大承重,物品有重量和价值。给定不同价值的物品,如何保证背包里的物品价值最大。
- 部门背包(物品可分割):某件物品是一堆,可以带走这件物品的一部分。
- 0-1背包(物品不可分割):对于某件物品,要么选中,要么不选中。
其中,部分背包问题可以使用贪心算法解决,并且能得到最优解。下面用一个例子举例说明:

- 因为物品可分割,按物品单位重量价值排序;
- 可得单位重量的物品价值A > B > C;
- 所以取A = 10kg,B = 20kg,C = 20kg,可保证背包中价值最高。
/**
* 贪心算法:部分背包
*/
public class BagDemo {
public void take(List<Goods> goodslist, double bag) {
// 对物品按照价值排序从高到低
List<Goods> goodslist2 = sort(goodslist);
double sum_w = 0;
// 取出价值最高的
for (int i = 0; i < goodslist2.size(); i++) {
sum_w += goodslist2.get(i).weight;
if (sum_w <= bag) {
System.out.println(goodslist2.get(i).name + "取" +
goodslist2.get(i).weight + "kg");
} else {
System.out.println(goodslist2.get(i).name + "取" + (bag - (sum_w - goodslist2.get(i).weight)) + "kg");
return;
}
}
}
// 按物品的每kg 价值排序 由高到低 price/weight
private List<Goods> sort(List<Goods> goodslist) {
goodslist.sort((o1, o2) -> (int) (o2.val - o1.val));
return goodslist;
}
public static void main(String[] args) {
BagDemo bd = new BagDemo();
Goods goods1 = new Goods("A", 10, 60);
Goods goods2 = new Goods("B", 20, 100);
Goods goods3 = new Goods("C", 30, 120);
List<Goods> goodslist = new ArrayList<>(){{add(goods2);add(goods3);add(goods1);}};
bd.take(goodslist, 50);
}
}
class Goods {
String name;
double weight;
double price;
double val;
public Goods(String name,double weight, double price) {
this.name=name;
this.weight = weight;
this.price = price;
val=price/weight;
}
}5.2、分治算法
分而治之,将原问题划分为n个规模较小,结构与原问题相似的子问题,递归解决这些子问题,然后再合并结果。(快速排序就用到了分治算法)。
当问题足够小时,可直接求解(递归结束条件)。
举例说明:将小写abcde转换成大写ABCDE。

public static char[] toUpCase(char[] chs,int i){
if (i >= chs.length) {
return chs;
}
chs[i] = toUpCaseUnit(chs[i]);
return toUpCase(chs,i+1);
}
public static char toUpCaseUnit(char c) {
int n=c;
if (n<97 || n>122){
return ' ';
}
return (char)Integer.parseInt(String.valueOf(n-32));
}
public static void main(String[] args) {
String ss="abcde";
System.out.println(Test.toUpCase(ss.toCharArray(),0));
}5.3、回溯算法
类似枚举的深度优先搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就"回溯"返回(递归返回),尝试别的路径。
万金油算法,穷举所有的情况,找到满足期望的解。时间复杂度为O(n!),指数级别,性能非常低。
经典的八皇后问题:

把这个问题划分成 8 个阶段,依次将 8 个棋子放到第一行、第二行、第三行……第八行。在放置的 过程中,我们不停地检查当前放法,是否满足要求。如果满足,则跳到下一行继续放置棋子;如果不满 足,那就再换一种放法,继续尝试。
/**
* 回溯算法:N皇后问题
*/
public class NQueens {
//皇后数
static int QUEENS = 8;
//下标表示行,值表示queen存储在哪一列
int[] result = new int[QUEENS];
/**
* 在每行放置Queen
*
* @param row
*/
public void setQueens(int row) {
//递归中断
if (row == QUEENS) {
printQueens();
return;
}
//在每行依次放置列 没有合适的则回到上一层
for (int col = 0; col < QUEENS; col++) {
if (isOk(row, col)) {
//设置列
result[row] = col;
//开始下一行
setQueens(row + 1);
}
}
}
/**
* 打印输出
*/
private void printQueens() {
for (int i = 0; i < QUEENS; i++) {
for (int j = 0; j < QUEENS; j++) {
if (result[i] == j) {
System.out.print("Q| ");
} else {
System.out.print("*| ");
}
}
System.out.println();
}
System.out.println("-----------------------");
}
/**
* 判断是否可以放置
*
* @param row 行
* @param col 列
* @return
*/
private boolean isOk(int row, int col) {
int leftup = col - 1;
int rightup = col + 1;
// 逐行往上考察每一行
for (int i = row - 1; i >= 0; i--) {
//列上存在queen
if (result[i] == col) return false;
//左上对角线存在queen
if (leftup >= 0) {
if (result[i] == leftup) return false;
}
//右下对角线存在queen
if (rightup < QUEENS) {
if (result[i] == rightup) return false;
}
leftup--;
rightup++;
}
return true;
}
public static void main(String[] args) {
NQueens queens=new NQueens();
queens.setQueens(0);
}
}5.4、动态规划
分阶段求解,通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推/分治的方式去解决。
三个概念:最优子结构、边界(初始值)、dp方程。
动态规划常用于算法实现中存在大量的重复子问题正好相反,动态规划之所以高效,就是因为回溯算法实现中存在大量的重复子问题。
5.4.1、斐波那契数列:

1)递归分治+记忆搜索(备忘录)
利用一个数组,来保存已经计算过的函数,减少递归过程中的重复计算。
//用于存储每次的计算结果
static int[] sub=new int[10];
public static int fib(int n){
if(n<=1) return n;
//没有计算过则计算
if(sub[n]==0){
sub[n]=fib(n-1)+fib(n-2);
}
//计算过直接返回
return sub[n];
}
public static void main(String[] args) {
System.out.println(fib(9));
}2)递推(dp方程)
dp方程:

if (i < 2):dp[0] = 0; dp[1] = 1;
if (i >= 2):dp[i] = dp[i-1] + dp[i-2]
- 最优子结构:fib[9]=finb[8]+fib[7]
- 边界:a[0]=0; a[1]=1;
- dp方程:fib[n]=fib[n-1]+fib[n-2]
public static int fib(int n){
int a[]=new int[n+1];
a[0]=0;
a[1]=1;
int i;
// a[n]= a[n-1]+a[n-2]
for(i=2;i<=n;i++){
a[i]=a[i-1]+a[i-2];
}
// i已经加1了,所以要减掉1
return a[i-1];
}
public static void main(String[] args) {
System.out.println(fib(9));
}以上内容为个人学习理解,如有问题,欢迎在评论区指出。文章来源:https://www.toymoban.com/news/detail-630447.html
部分内容截取自网络,如有侵权,联系作者删除。文章来源地址https://www.toymoban.com/news/detail-630447.html
到了这里,关于算法基础简介的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!