数据结构 | 树的定义及实现

这篇具有很好参考价值的文章主要介绍了数据结构 | 树的定义及实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、树的术语及定义

二、树的实现

2.1 列表之列表

2.2 节点与引用

一、树的术语及定义

节点：

节点是树的基础部分。它可以有自己的名字，我们称作“键”。节点也可以带有附加信息，我们称作“有效载荷”。有效载荷信息对于很多树算法来说不是重点，但它常常在使用树的应用中很重要。

边：
边是树的另一个基础部分。两个节点通过一条边相连，表示他们之间存在关系。除了根节点以外，其他每个节点都仅有一条入边，出边则可能有多条。

根节点：

根节点是树中唯一没有入边的节点。

路径：

路径是由边连接的有序节点列表。比如，哺乳纲食肉目猫科猫属家猫就是一条路径。

子节点：

一个节点通过出边和子节点相连。

父节点：

一个节点是其所有子节点的父节点。

兄弟节点：

具有同一父节点的节点互称为兄弟节点。

子树：

一个父节点及其所有后代的节点和边构成一颗子树。

叶子节点：

叶子节点没有子节点。

层数：

节点n的层数是从根节点到n的唯一路径长度。根节点的层数是0。

高度：

树的高度是其中节点层数的最大值。

定义基本术语后，就可以进一步给出树的正式定义。实际上，下面提供了两种定义，其中一种涉及节点和边，另一种涉及递归。递归定义很有用。

定义一：树由节点及连接节点的边构成。树有以下属性：

有一个根节点；
除根节点外，其他每个节点都与其唯一的父节点相连；
从根节点到其他每个节点都有且仅有一条路径；
如果每个节点最多有两个子节点，我们就称这样的树为二叉树。

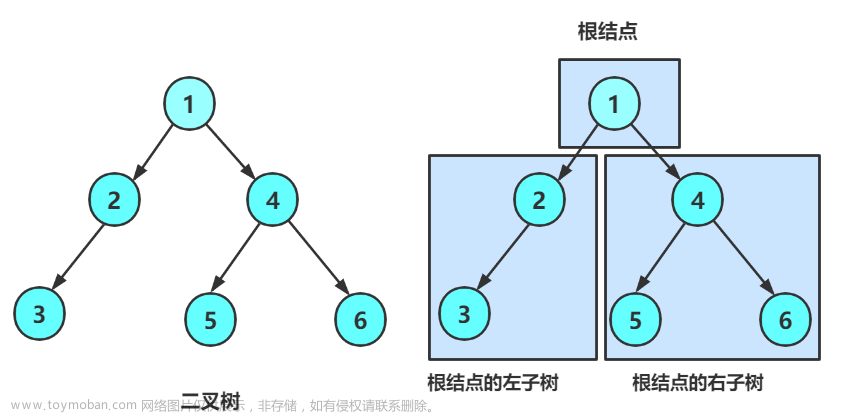
定义二：一棵树要么为空，要么由一个根节点和零颗或多颗子树构成，子树本身也是一棵树。每颗子树的根节点通过一条边连到父树的根节点。

二、树的实现

根据上面的定义，可以使用以下函数创建并操作二叉树。

BinaryTree()创建一个二叉树实例。
getLeftChild()返回当前节点的左子节点所对应的二叉树。
getRightChild()返回当前节点的右子节点所对应的二叉树。
setRootVal(val)在当前节点中存储参数val中的对象。
getRootVal()返回当前节点存储的对象。
insertLeft(val)新建一颗二叉树，并将其作为当前节点的左子节点。
insertRight(val)新建一颗二叉树，并将其作为当前节点的右子节点。

实现树的关键在于选择一个好的内部存储技巧。Python提供两种有意思的方式，我们在选择前会仔细了解这两种方式。第一种称作“列表之列表”，第二种称作“节点与引用”。

2.1 列表之列表

在“列表之列表”的树中，我们将根节点的值作为列表的第一个元素；第二个元素是代表左子树的列表；第三个元素是代表右子树的列表。

myTree=['a', #根节点
        ['b', #左子树
         ['d',[],[]],
         ['e',[],[]] ],
        ['c', #右子树
         ['f',[],[]],
         [] ]
       ]

注意，可以通过标准的列表切片操作访问子树。树的根节点是myTree[0]，左子树是myTree[1]，右子树是myTree[2]。“列表之列表”表示法有个很好的性质，那就是表示子树的列表结构很符合树的定义，这样的结构是递归的！由一个根节点和两个空列表构成的子树是一个叶子节点。还有一个很好的性质，那就是这种表示法可以推广到有很多子树的情况。如果树不是二叉树，则多一个子树只是多一个列表。

数据结构 | 树的定义及实现,数据结构,数据结构,树,二叉树,python

接下来提供一些便于将列表作为树使用的函数，以正式定义树数据结构。注意，我们不是要定义二叉树类，而是要创建可用于标准列表的函数。

列表的函数BinaryTree：

def BinaryTree(r):
    return [r,[],[]]

BinaryTree函数构造一个简单的列表，它仅有一个根节点和两个作为子节点的空列表。要给树添加左子树，需要在列表的第二个位置加入一个新的列表。请务必当心：如果列表的第二个位置已经有内容了，我们要保留已有内容，并将它作为新列表的左子树。

插入左子树的Python代码：

def insertLeft(root,newBranch):
    t=root.pop(1)
    if len(t)>1:
        root.insert(1,[newBranch,t,[]])
    else:
        root.insert(1,[newBranch,[],[]])
    return root

插入右子树的Python代码：

def insertRight(root,newBranch):
    t=root.pop(2)
    if len(t)>1:
        root.insert(2,[newBranch,[],t])
    else:
        root.insert(2,[newBranch,[],[]])
    return root

为了完整地创建树的函数集，我们编写一些访问函数，用于读写根节点与左右子树。

树的访问函数代码：

def getRootVal(root):
    return root[0]

def setRootVal(root,newVal):
    root[0]=newVal

def getLeftChild(root):
    return root[1]

def getRightChild(root):
    return root[2]

数据结构 | 树的定义及实现,数据结构,数据结构,树,二叉树,python

2.2 节点与引用

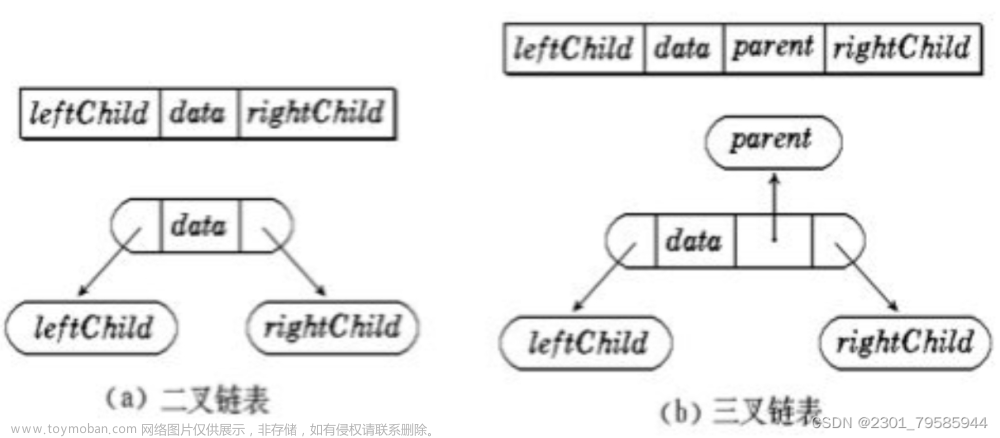
树的第二种表示法是利用节点与引用。我们将定义一个类，其中有根节点和左右子树的属性。这种表示法遵循对象编程范式。

#BinaryTree类
class BinaryTree:
    def __init__(self,rootObj):
        self.key=rootObj
        self.leftChild=None
        self.rightChild=None
    
    #插入左子节点
    def insertLeft(self,newNode):
        if self.leftChild==None:
            self.leftChild=BinaryTree(newNode)
        else:
            t=BinaryTree(newNode)
            t.left=self.leftChild
            self.leftChild=t
    
    #插入右子节点
    def insertRight(self,newNode):
        if self.rightChild==None:
            self.rightChild=BinaryTree(newNode)
        else:
            t=BinaryTree(newNode)
            t.right=self.rightChild
            self.rightChild=t
    
    #二叉树的访问函数
    def getRightChild(self):
        return self.rightChild
    
    def getLeftChild(self):
        return self.leftChild
    
    def setRootVal(self,obj):
        self.key=obj
        
    def getRootVal(self):
        return self.key

数据结构 | 树的定义及实现,数据结构,数据结构,树,二叉树,python 文章来源地址https://www.toymoban.com/news/detail-630759.html