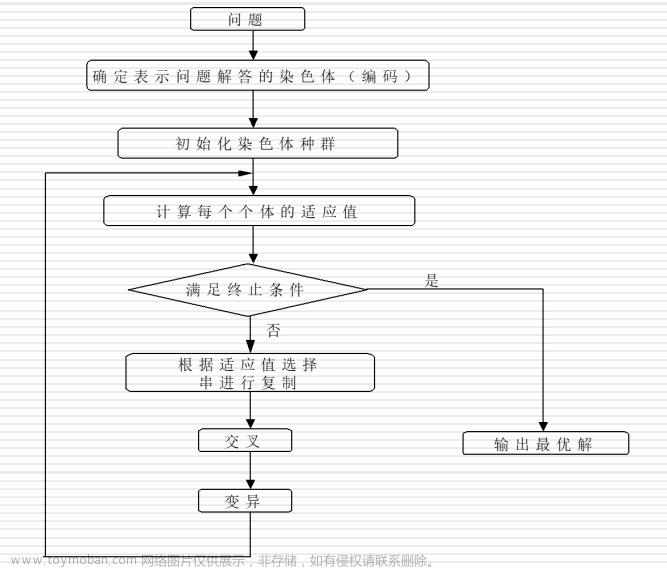
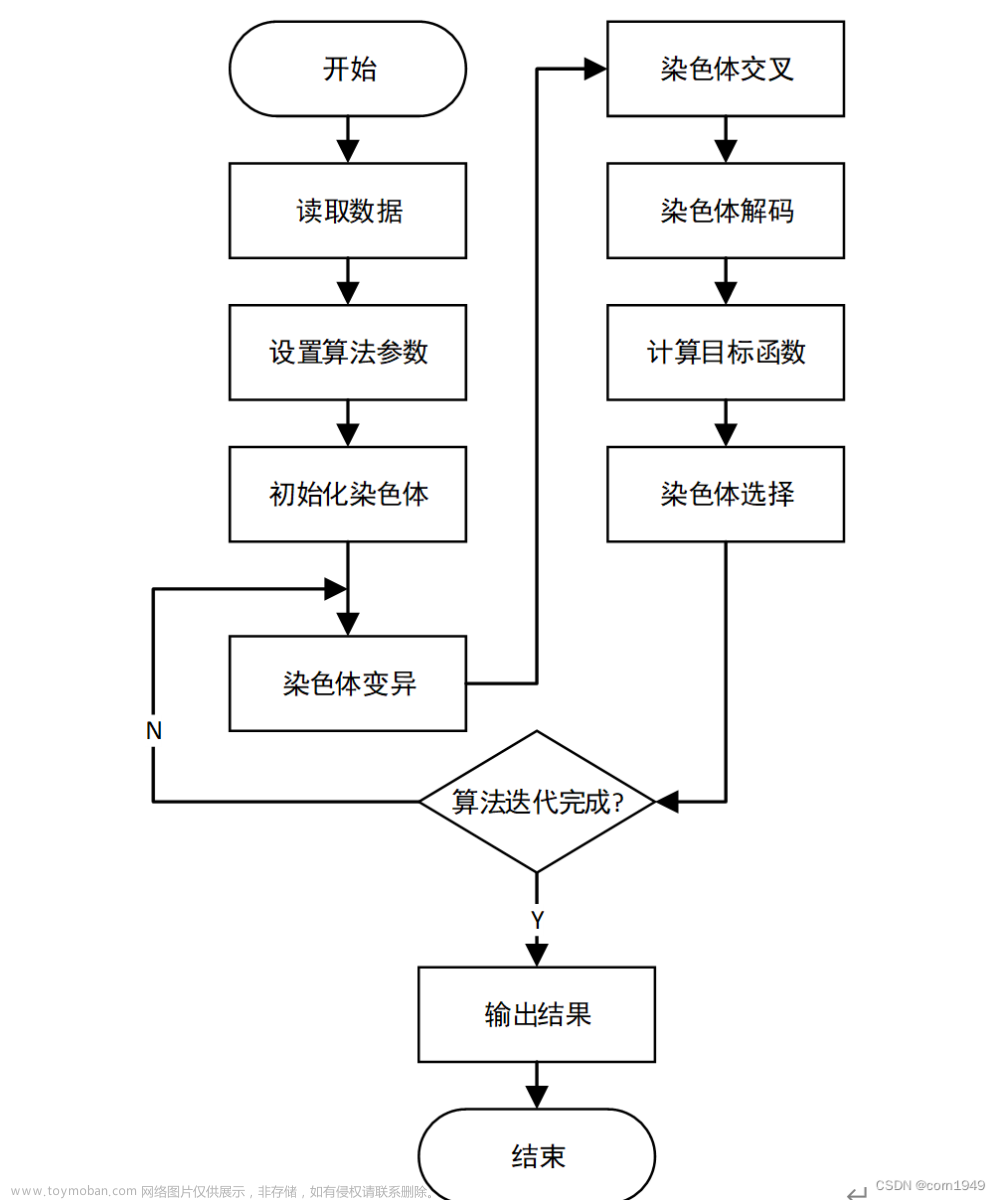
上次懂了遗传算法最基本的原理,就写了这样一点总结与理解,那么最开始学都是最简单的,小白易懂的遗传算法(Python代码实现)那么现在要加上约束条件了,约束条件我一直不知道套在遗传算法的哪个模块,然后我又发现了一篇很好的文章,遗传算法求解带约束优化问题(源码实现)带我走进了有约束的遗传算法的大门,相信大家也可以看懂的,顺便安利一个软件,Pycharm的debug功能超好用,尤其是学习别人的代码,哪里不懂就在哪里设置断点,看一下每一个变量此时的取值,帮助你快速理解这个代码实现的功能。
回归正题,回到有约束的求解问题,
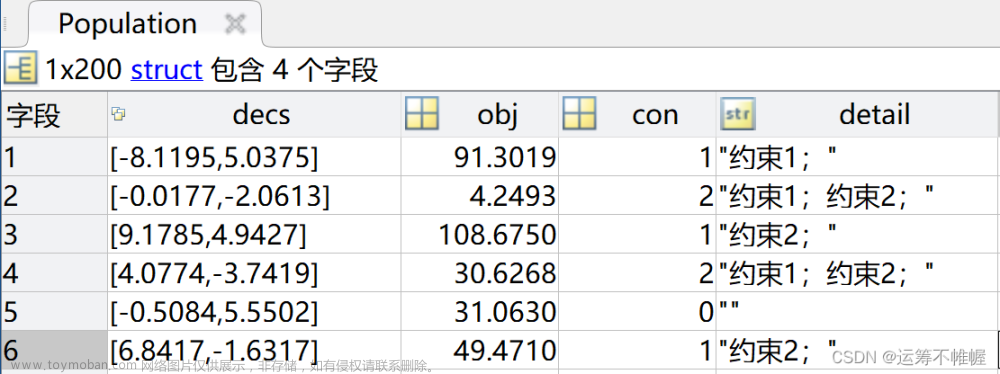
如上,有两个变量,如果采用二进制编码的话,可能染色体比较长,然后就采用了实数编码的方式,一共就两个基因位,一个是x,一个是y。
约束条件的解决办法就是变成惩罚项,加到适应度函数里面,如果某个个体不满足约束条件,那就要对目标函数做一些惩罚。
对于这里采用的惩罚函数,因为约束条件都是小于0的,而且目标函数是求最小值,那么如果不满足约束条件的话,那这个惩罚项就是个正数,把他加到目标函数上面,也就是不利于目标函数取得最小值,那么如果满足约束条件的话,那这个惩罚项就是个负数,但他只是满足了约束条件的基本要求,也不能真的减小目标函数,所以就让目标函数+0,也就是保持不变。
def calc_f(pop): ##这是生成一个种群的目标函数值
"""计算群体粒子的目标函数值,X 的维度是 size * 2 """
a = 10
pi = np.pi
x = pop[:, 0]
y = pop[:, 1]
return 2 * a + x ** 2 - a * np.cos(2 * pi * x) + y ** 2 - a * np.cos(2 * 3.14 * y)
def calc_e(pop): ##生成一个种群的惩罚函数值总和
"""计算群体粒子的目惩罚项,X 的维度是 size * 2 """
sumcost = []
for i in range(pop.shape[0]):
ee = 0
"""计算第一个约束的惩罚项"""
e1 = pop[i, 0] + pop[i, 1] - 6
ee += max(0, e1)
"""计算第二个约束的惩罚项"""
e2 = 3 * pop[i, 0] - 2 * pop[i, 1] - 5
ee += max(0, e2)
sumcost.append(ee)
return sumcost
选择、交叉和变异操作,以及子代和父代的选择,对于这里需要注意的就是,他并没有在每一次交叉(或者变异)之后都有对自变量是否满足上下限的一个判断,但是并没有根据适应度值比较产生的子代和原本父代的优劣,这样显得有点冗余,所以就只是在交叉变异完得到的新种群,与上一代种群进行了比较,并且是针对每一个个体进行比较,所以说最终产生的这个种群是父代与子代的结合。文章来源:https://www.toymoban.com/news/detail-630821.html
def select(pop, fitness):
"""根据轮盘赌法选择优秀个体"""
fitness = 1 / fitness # fitness越小表示越优秀,被选中的概率越大,做 1/fitness 处理
fitness = fitness / fitness.sum() # 归一化
idx = np.arange(NP)
pop2_idx = np.random.choice(idx, size=NP, p=fitness) # 根据概率选择
pop2 = pop[pop2_idx, :] ##把适应度高的个体给选择出来组成pop2
return pop2
def crossover(pop, Pc):
"""按顺序选择2个个体以概率c进行交叉操作"""
for i in range(0, pop.shape[0], 2):
parent1 = pop[i].copy() # 父亲
parent2 = pop[i + 1].copy() # 母亲
# 产生0-1区间的均匀分布随机数,判断是否需要进行交叉替换
if np.random.rand() <= Pc:
child1 = (1 - Pc) * parent1 + Pc * parent2 # 这是实数编码 的交叉形式 shape(2,)
# child1=child1.reshape(-1,2)
child2 = Pc * parent1 + (1 - Pc) * parent2 # shape(2,)
# child2=child2.reshape(1,2)
# 判断个体是否越限
if child1[0] > Xmax or child1[0] < Xmin:
child1[0] = np.random.uniform(Xmin, Xmax)
if child1[1] > Ymax or child1[1] < Ymin:
child1[1] = np.random.uniform(Ymin, Ymax)
if child2[0] > Xmax or child2[0] < Xmin:
child2[0] = np.random.uniform(Xmin, Xmax)
if child2[1] > Ymax or child2[1] < Ymin:
child2[1] = np.random.uniform(Ymin, Ymax)
######通过比较父辈和子代的适应度值和惩罚项 来决定要不要孩子
pop[i, :] = child1
pop[i + 1, :] = child2
return pop
def mutation(pop, Pm):
"""变异操作"""
for i in range(NP): # 遍历每一个个体
# 产生0-1区间的均匀分布随机数,判断是否需要进行变异
parent = pop[i].copy() # 父辈
if np.random.rand() <= Pm:
child = np.random.uniform(-1, 2, (1, 2)) # 用随机赋值的方式进行变异 得到子代 就跟初始化的赋值规则是一样的
# 判断个体是否越限
if child[:, 0] > Xmax or child[:, 0] < Xmin:
child[:, 0] = np.random.uniform(Xmin, Xmax)
if child[:, 1] > Ymax or child[:, 1] < Ymin:
child[:, 1] = np.random.uniform(Ymin, Ymax)
######通过比较父辈和子代的适应度值和惩罚项 来决定要不要孩子
pop[i] = child
return pop
# 子代和父辈之间的选择操作
def update_best(parent, parent_fitness, parent_e, child, child_fitness, child_e):
"""
判
:param parent: 父辈个体
:param parent_fitness:父辈适应度值
:param parent_e :父辈惩罚项
:param child: 子代个体
:param child_fitness 子代适应度值
:param child_e :子代惩罚项
:return: 父辈 和子代中较优者、适应度、惩罚项
"""
# 规则1,如果 parent 和 child 都没有违反约束,则取适应度小的
if parent_e <= 0.0000001 and child_e <= 0.0000001:
if parent_fitness <= child_fitness:
return parent, parent_fitness, parent_e
else:
return child, child_fitness, child_e
# 规则2,如果child违反约束而parent没有违反约束,则取parent
if parent_e < 0.0000001 and child_e >= 0.0000001:
return parent, parent_fitness, parent_e
# 规则3,如果parent违反约束而child没有违反约束,则取child
if parent_e >= 0.0000001 and child_e < 0.0000001:
return child, child_fitness, child_e
# 规则4,如果两个都违反约束,则取适应度值小的
if parent_fitness <= child_fitness:
return parent, parent_fitness, parent_e
else:
return child, child_fitness, child_e
遗传算法主体文章来源地址https://www.toymoban.com/news/detail-630821.html
import numpy as np
import matplotlib.pyplot as plt
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
####################初始化参数#####################
NP = 50 # 种群数量
L = 2 # 对应x,y
Pc = 0.5 # 交叉率
Pm = 0.1 # 变异率
G = 100 # 最大遗传代数
Xmax = 2 # x上限
Xmin = 1 # x下限
Ymax = 0 # y上限
Ymin = -1 # y 下限
best_fitness = [] # 记录每次迭代的效果
best_xy = [] # 存放最优xy
pop = np.random.uniform(-1, 2, (NP, 2)) # 初始化种群 (生成-1,2之间的随机数)shape (NP,2)
for i in range(G): # 遍历每一次迭代
fitness = np.zeros((NP, 1))# 存放适应度值 实现同样效果的方法还可以写成 fitness = np.array([0]*NP)
ee = np.zeros((NP, 1)) # 存放惩罚项值 ee = np.array([0]*NP)
parentfit = calc_f(pop) # 计算父辈目标函数值
parentee = calc_e(pop) # 计算父辈惩罚项
# parentfitness = get_fitness(pop) # 计算父辈适应度值 适应度值=目标函数值+惩罚项
parentfitness = parentfit + parentee
print(parentfitness )
pop1 = select(pop, parentfitness) # 选择
pop2= crossover(pop1, Pc) # 交叉
pop3 = mutation(pop2, Pm) # 变异 这是选择、交叉、变异完最终的子代,
childfit = calc_f(pop3) # 子代目标函数值
childee = calc_e(pop3) # 子代惩罚项
# childfitness = get_fitness(pop) # 子代适应度值
childfitness = childfit + childee
# 更新群体,看看保留子代还是父代
for j in range(NP): # 遍历每一个个体,使每一个个体产生的子代和父代比较,哪个好就保留哪个,最后组成一个新的种群参与后面的迭代
pop[j], fitness[j], ee[j] = update_best(pop[j], parentfitness[j], parentee[j], pop3[j], childfitness[j],childee[j])
best_fitness.append(fitness.min()) ###在保留下来的这个种群里面再挑一个适应度最小的作为最优解
x, y = pop[fitness.argmin()]
best_xy.append((x, y))
# 多次迭代后的最终效果
print("最优值是:%.5f" % best_fitness[-1])
print("最优解是:x=%.5f, y=%.5f" % best_xy[-1])
# 打印效果
plt.plot(best_fitness, color='r')
plt.show()
到了这里,关于有约束的遗传算法(Python代码实现)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!