王道408---数据结构--用数组实现二叉树--并查集及其优化代码-Toy模板网

这篇具有很好参考价值的文章主要介绍了王道408---数据结构--用数组实现二叉树--并查集及其优化代码。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

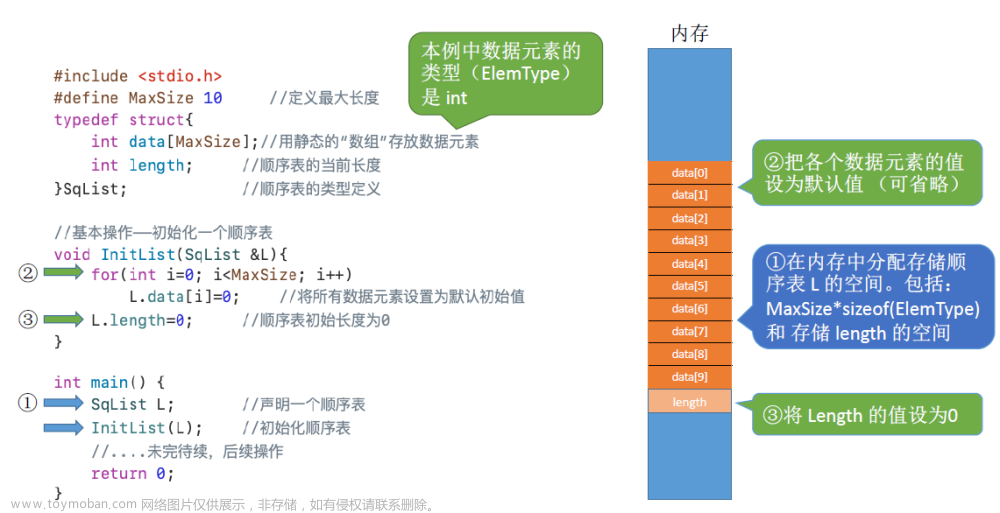
一、数组实现二叉树(下标从0开始)

#include <stdio.h>
typedef struct _TreeNode{
    int data;
    bool IsEmpty;       //结点是否为空  // 因为我们的二叉树不一定是满二叉树，中间可能有一些节点不存在 // 值为1代表空
}TreeNode;


// 初始化
void InitTreeNode(TreeNode t[],int len){
    for(int i=0;i<len;i++)
        t[i].IsEmpty = 1;
}


bool IsEmpty(TreeNode t[],int len,int idx){
    if(idx >= len || idx < 0) return 1;         // 修改为0
    
    return t[idx].IsEmpty;
}

// father = (child-1)/2   or  father = child/2 - 1
int findFather(TreeNode t[],int len,int idx){
    if(idx == 0) return -1;         //特判根节点没有父节点      // 特判也修改为0
    int fatheridx = (idx-1) / 2;
    if(IsEmpty(t,len,fatheridx)) return -1;
    return fatheridx;
}

// lchild = father*2 + 1
int findLchild(TreeNode t[],int len,int idx){
    int lchild = idx*2 + 1;
    if(IsEmpty(t,len,lchild)) return -1;
    return lchild;
}

// rchild = father*2+2
int findRchild(TreeNode t[],int len,int idx){
    int rchild = idx*2 + 2;
    if(IsEmpty(t,len,rchild)) return -1;
    return rchild; 
}

//实现前序遍历, 从下表为idx的节点开始前序遍历
int PreorderTree(TreeNode t[],int len,int idx){
    if(IsEmpty(t,len,idx)) return 0;
    printf("%d\n",t[idx].data);
    PreorderTree(t,len,findLchild(t,len,idx));
    PreorderTree(t,len,findRchild(t,len,idx));
    return 0;
}

int InorderTree(TreeNode t[],int len,int idx){
    if(IsEmpty(t,len,idx)) return 0;
    InorderTree(t,len,findLchild(t,len,idx));
    printf("%d\n",t[idx].data);
    InorderTree(t,len,findRchild(t,len,idx));
    return 0;
}
int PostorderTree(TreeNode t[],int len,int idx){
    if(IsEmpty(t,len,idx)) return 0;
    PostorderTree(t,len,findLchild(t,len,idx));
    PostorderTree(t,len,findRchild(t,len,idx));
    printf("%d\n",t[idx].data);
    return 0;
}


int main(){
    TreeNode Td[100];            // 这里的二叉树节点要从0开始
    int fatheridx;
    int testLen = 7;          // IsEmpty 的判断是 >=Len 所以这里加一个1
    for(int i=0;i<=testLen;i++){
        Td[i].data = i+1;
        Td[i].IsEmpty = 0;
    }
    PreorderTree(Td,testLen,0);
    // InorderTree(Td,testLen,0);
    // PostorderTree(Td,testLen,0);
    return 0;
}

二、数组实现二叉树(下标从1开始)

#include <stdio.h>
typedef struct _TreeNode{
    int data;
    bool IsEmpty;       //结点是否为空  // 因为我们的二叉树不一定是满二叉树，中间可能有一些节点不存在 // 值为1代表空
}TreeNode;


// 初始化
void InitTreeNode(TreeNode t[],int len){
    for(int i=0;i<len;i++)
        t[i].IsEmpty = 1;
}


bool IsEmpty(TreeNode t[],int len,int idx){
    if(idx >= len || idx < 1) return 1;
    
    return t[idx].IsEmpty;
}

// father = child / 2
int findFather(TreeNode t[],int len,int idx){
    // if(idx == 1) return -1;         //特判根节点没有父节点 ，不加也没事，但下表从0开始的时候必须加
    int fatheridx = idx / 2;
    if(IsEmpty(t,len,fatheridx)) return -1;
    return fatheridx;
}

// lchild = father*2
int findLchild(TreeNode t[],int len,int idx){
    int lchild = idx*2;
    if(IsEmpty(t,len,lchild)) return -1;
    return lchild;
}

// rchild = father*2+1
int findRchild(TreeNode t[],int len,int idx){
    int rchild = idx*2+1;
    if(IsEmpty(t,len,rchild)) return -1;
    return rchild; 
}

//实现前序遍历, 从下表为idx的节点开始前序遍历
int PreorderTree(TreeNode t[],int len,int idx){
    if(IsEmpty(t,len,idx)) return 0;
    printf("%d\n",t[idx].data);
    PreorderTree(t,len,findLchild(t,len,idx));
    PreorderTree(t,len,findRchild(t,len,idx));
    return 0;
}

int InorderTree(TreeNode t[],int len,int idx){
    if(IsEmpty(t,len,idx)) return 0;
    InorderTree(t,len,findLchild(t,len,idx));
    printf("%d\n",t[idx].data);
    InorderTree(t,len,findRchild(t,len,idx));
    return 0;
}
int PostorderTree(TreeNode t[],int len,int idx){
    if(IsEmpty(t,len,idx)) return 0;
    PostorderTree(t,len,findLchild(t,len,idx));
    PostorderTree(t,len,findRchild(t,len,idx));
    printf("%d\n",t[idx].data);
    return 0;
}


int main(){
    TreeNode Td[100];            // 这里的二叉树节点要从一开始
    int fatheridx;
    int testLen = 7+1;          // IsEmpty 的判断是 >=Len 所以这里加一个1
    for(int i=1;i<=testLen;i++){
        Td[i].data = i;
        Td[i].IsEmpty = 0;
    }
    PreorderTree(Td,testLen,1);
    // InorderTree(Td,testLen,1);
    // PostorderTree(Td,testLen,1);
    return 0;
}

三、并查集及其优化思路

#include <stdio.h>
#define MAXSIZE 50
int UFSets[MAXSIZE];

void InitUFSets(int S[]){
    for(int i=0;i<MAXSIZE;i++){
        S[i] = -1;
    }
}

int find(int S[],int x){
    if(S[x] == -1) return x;           // -1说明到底了
    return find(S,S[x]);
}

int pathCompFind(int S[],int x){         // 路径压缩策略优化Find 操作
    if(S[x] >= 0){
        S[x] = find(S,S[x]); 
        return S[x];
    }
    return x;
}


bool UnionElem(int S[],int elem1,int elem2){    //王道书上是直接合并的root，而不是元素成员
    int first = find(S,elem1);
    int second = find(S,elem2);
    if(first != second){
        printf("%d -- %d\n",first,second);
        S[second] = first;
        return 1;
    }
    return 0;
}

bool UnionRoot(int S[],int Root1,int Root2){
    if(Root1 == Root2) return 0;    //比较两个根是否来自同一集合
    S[Root2] = Root1;               // 将根Root2连接到Root1上
    return 1;
}

bool optUnionRoot(int S[],int Root1,int Root2){
    if(Root1 == Root2) return 0;
    if(S[Root2] > S[Root1]){   // Root2 结点数更少         // 因为初始化的时候S的值全为 -1  所以 若S[Root1]与S[Root2]相加后为更小的负数
                                                            //较小的树，树较大，这也是为什么 S[Root1] >= S[Root2]时 却把Root2合并到Root1中的原因
        S[Root1] += S[Root2];       // 累加节点个数
        S[Root2] = Root1;
    }else{
        S[Root2] += S[Root1];
        S[Root1] = Root2;
    }
    return 1;
}

void debug(){
    for(int i=0;i<MAXSIZE;i++){
        printf("%d ",UFSets[i]);
    }
    puts("");
}

int main(){
    InitUFSets(UFSets);
    int arr[100] = {0,1,2,3,4,5,6,7,8,9};
    for(int i=0;i<=10;i++){
        UnionElem(UFSets,arr[i*2],arr[i*2+1]);
        // 0 -- 1
        // 2 -- 3
        // 4 -- 5
        // 6 -- 7
        // 8 -- 9
    }
    UnionElem(UFSets,1,3);
    UnionElem(UFSets,5,7);
    // 0 -- 1
    // 2 -- 3
    // 4 -- 5
    // 6 -- 7
    // 8 -- 9
    // 0 -- 2
    // 4 -- 6

    UnionElem(UFSets,1,6);
    UnionElem(UFSets,2,7);
    // debug();



    return 0;
}