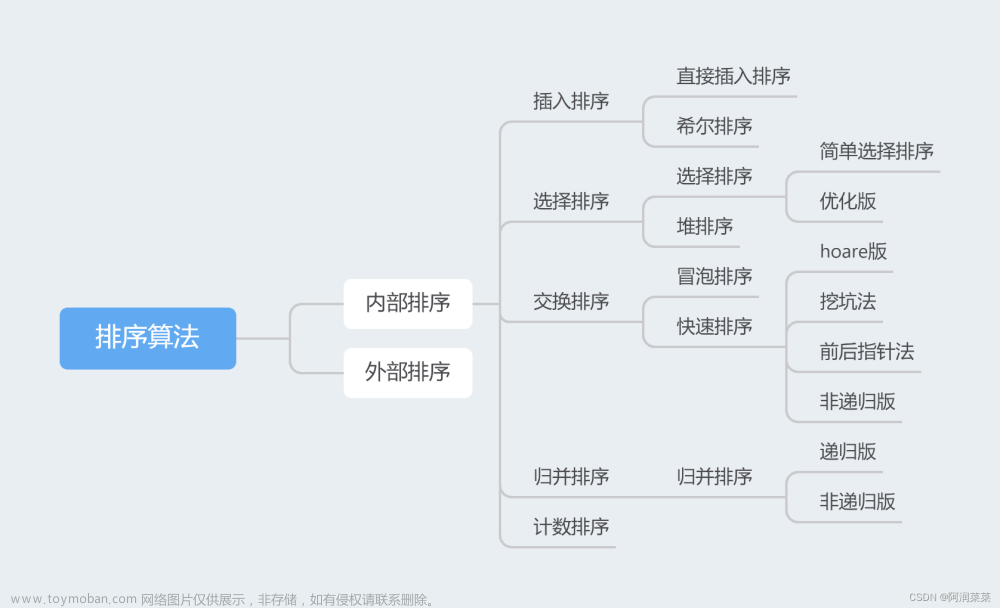
一. 字符串
1. 字符串变形
描述: 对于一个长度为 n 字符串,我们需要对它做一些变形。
首先这个字符串中包含着一些空格,就像"Hello World"一样,然后我们要做的是把这个字符串中由空格隔开的单词反序,同时反转每个字符的大小写。
示例1
输入:
“This is a sample”,16
返回值:
“SAMPLE A IS tHIS”
// 思路:
// 1. 将字符串用split(' ')按照空格符分割成数组
// 2. 将数组翻转,判断每一个项中每一个字母的大小写,如果是大写改为小写,如果是小写改为大写,生成一个新数组
// 3. 将新数组用join拼接成一个字符串
// 4. 注意:
// split():默认按照空格分隔,会把多个空格当成一个分隔符。
// split(' '):按照空格分隔,会把每一个空格都当成一个分隔符。
// split(''):将每一个字符串都分隔。
const str = 'Hello World This Is a Student'
function trans(str, num){
if(str.length != num)return '数组的长度有误!'
const arrReverse = str.split(' ').reverse()
return arrReverse.map(item => {
// 进行大小写的转换
return [...item].map(ele => ele == ele.toLowerCase() ? ele.toUpperCase() : ele.toLowerCase()).join('')
}).join(' ')
}
console.log(trans(str,29)) // sTUDENT A iS tHIS wORLD hELLO
2. 字符串最长公共前缀
描述:给你一个大小为 n 的字符串数组 strs ,其中包含n个字符串 , 编写一个函数来查找字符串数组中的最长公共前缀,返回这个公共前缀。
示例1
输入:[“abc”]
返回值:“abc”
示例2
输入:[“abca”,“abc”,“abca”,“abc”,“abcc”]
返回值:“abc”
// 思路:
// 1. 如果数组长度为0,则返回空字符串
// 2. 如果数组长度为1,则返回数组中的字符串
// 3. 将数组排序,用第一个元素的第一个字符和最后一个元素的第一个字符进行比较
// 4. 如果相同将这个字符保存下来,以此类推将每次的字符串拼接起来,直到比较的两个字符串不相同,终止循环,最后返回拼接后的字符串
const strArr = ["abca","abc","abca","abc","abcc"]
function longestCommonPrefix(strArr){
if(!strArr.length) return ''
if(strArr.length === 1) return strArr[0]
strArr.sort()
const firstStr = strArr[0]
const lastStr = strArr.pop()
let res = ''
for(let i=0;i<firstStr.length;i++){
if(firstStr[i] == lastStr[i]){
res += firstStr[i]
}else{
break
}
}
return res
}
3. 验证ip地址
描述:给定一个ip地址,判断是ip4地址还是ip6地址
IPv4 地址由四组十进制数和点来表示,每个地址包含4个十进制数,其范围为 0 - 255, 用(“.”)分割。比如,172.16.254.1;
同时,IPv4 地址内的数不会以 0 开头。比如,地址 172.16.254.01 是不合法的。
IPv6 地址由8组16进制的数字来表示,每组表示 16 比特。这些组数字通过 (“:”)分割。只支持大小写和0-9的数字,不能出现特殊字符和空格
示例1
输入:“172.16.254.1”
返回值:“IPv4”
说明:这是一个有效的 IPv4 地址, 所以返回 “IPv4”
示例2
输入:“2001:0db8:85a3:0:0:8A2E:0370:7334”
返回值:“IPv6”
说明:这是一个有效的 IPv6 地址, 所以返回 “IPv6”
示例3
输入:“256.256.256.256”
返回值:“Neither”
说明:这个地址既不是 IPv4 也不是 IPv6 地址
// 思路:
// 1. 对输入的字符串先判断是属于ipv4范畴的还是ipv6范畴的
// 2. 如果属于ipv4范畴进行ipv4的判定,如果属于ipv6范畴进行ipv6判定。否则直接返回 Neither
// 3. 对于ipv4的判定:
// (1)先使用split('.')分割成数组,对数组长度判断,如果长度不为4,则返回 Neither。否则对数组里面的每一项是一个字符串进行判断
// (2)如果字符串长度为0或者大于3则返回false,否则对字符串每一项判断
// (3)如果字符串的第一项是'0'则返回false,否则如果不在'0'和'9'之间也返回false
// (4) 将这个字符串转成数字,如果不在0-255之间返回false,否则返回true
// 4. 对于ipv6的判定:
// (1) 先试用split(':')分割成数组,对数组长度判断,如果长度不为8,则返回 Neither,否则对数组里面的每一项是一个字符串进行判断
// (2) 如果字符串长度为0或者大于4则返回false,否则对字符串每一项判断
// (3)如果每一项的字符不在'0'--'9'、 'a'--'z' 、 'A'--'Z'之间则返回false,否则返回true
// 定义判断ipv4的方法:
function checkIPv4(s){
if(s.length === 0 || s.length > 3) return false
if(s[0] === '0') return false
for(let i of s){
if(i > '9' || i < '0') return false
}
return Number(s) <= 255 && Number(s) > 0
}
// 定义判断ipv6的方法:
function checkIPv6(s){
if(s.length === 0 || s.length > 4) return false
for(let j of s){
if(!(j>='0' && j<='9' || j>='a' && j<='f' || j>='A' && j<='F')) return false
}
return true
}
function solve(IP){
if(IP.indexOf('.') != -1){
const arrIpv4 = IP.split('.')
if(arrIpv4.length != 4) return 'Neither'
for(let ip of arrIpv4){
if(!checkIPv4(ip)){
return 'Neither'
}
}
return 'IPv4'
}else if(IP.indexOf(':') != -1){
const arrIpv6 = IP.split(':')
if(arrIpv6.length != 8) return 'Neither'
for(let ip of arrIpv6){
if(!checkIPv6(ip)){
return 'Neither'
}
}
return 'IPv6'
}else{
return 'Neither'
}
}
4. 大数相加
描述:以字符串的形式读入两个数字,编写一个函数计算它们的和,以字符串形式返回。
数据范围:长度小于等于100000,字符串仅由’0’-'9’构成
要求:时间复杂度O(n)
示例1
输入:“1”,“99”
返回值:“100”
说明:1+99=100
示例2
输入:“114514”,“”
返回值:“114514”
// 思路:
// 1. 对于一个很大的数来说不可以直接采用 Number()转成数字再相加,再用String(),因为这时候会丢失精度
// 2. 当两个数位数不一样的时候,分割成数组,在小的那个数前面补位'0',直到对齐
// 3. 从后往前加,做进位处理。如果大于9,则取余数,将余数用unshift()放进一个空数组的前面。同时记录一个变量为1。下次相加的时候加上这个变量
// 如果不大于9,则将这个数放进数组的前面
// 4. 最后将得到的数组用join()方法拼接成一个字符串
function solve(s,t){
const arr1 = s.split('')
const arr2 = t.split('')
let resArr = [], go = 0
while(arr1.length || arr2.length){
let num1 = +arr1.pop() || 0
let num2 = +arr2.pop() || 0
let temp = num1 + num2 + go
if(temp > 9){
temp %= 10
go = 1
}else{
go = 0
}
resArr.unshift(temp)
}
if (go) resArr.unshift(1);
return resArr.join('')
}
二. 堆、栈、队列
1. 用两个栈实现队列
描述:用两个栈来实现一个队列,使用n个元素来完成 n 次在队列尾部插入整数(push)和n次在队列头部删除整数(pop)的功能。 队列中的元素为int类型。保证操作合法,即保证pop操作时队列内已有元素。
数据范围:n<=1000
要求:存储n个元素的空间复杂度为 O(n) ,插入与删除的时间复杂度都是 O(1)
示例1
输入:[“PSH1”,“PSH2”,“POP”,“POP”]
返回值:1,2
说明:BinarySearchTree
“PSH1”:代表将1插入队列尾部
“PSH2”:代表将2插入队列尾部
"POP“:代表删除一个元素,先进先出=>返回1
"POP“:代表删除一个元素,先进先出=>返回2
// 方法一:
// 思路:
// 1. 定义两个空栈
// 2. 将数字push进第一个栈,然后再将pop出来的值push进第二个栈。最后在pop出来
// let arr2 = [],
// arr1 = [];
// function push(node)
// {
// // write code here
// arr1.push(node);
// }
// function pop()
// {
// // write code here
// if(!arr2.length){
// while(arr1.length){
// arr2.push(arr1.pop())
// }
// }
// return arr2.pop();
// }
// 方法二:
// 思路:
// 1. 定义一个空栈
// 2. 先将值push进去,然后再shift从头部删除值
let queue = [];
function push(node)
{
return queue.push(node);
}
function pop()
{
return queue.shift();
}
2. 包含Min函数的栈
描述:定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的 min 函数,输入操作时保证 pop、top 和 min 函数操作时,栈中一定有元素。
此栈包含的方法有:
push(value):将value压入栈中
pop():弹出栈顶元素
top():获取栈顶元素
min():获取栈中最小元素
示例:
输入: [“PSH-1”,“PSH2”,“MIN”,“TOP”,“POP”,“PSH1”,“TOP”,“MIN”]
输出: -1,2,1,-1
解析:
"PSH-1"表示将-1压入栈中,栈中元素为-1
"PSH2"表示将2压入栈中,栈中元素为2,-1
“MIN”表示获取此时栈中最小元素==>返回-1
"TOP"表示获取栈顶元素==>返回2
"POP"表示弹出栈顶元素,弹出2,栈中元素为-1
"PSH1"表示将1压入栈中,栈中元素为1,-1
"TOP"表示获取栈顶元素==>返回1
“MIN”表示获取此时栈中最小元素==>返回-1
// 思路:
// 1. 定义一个空栈
// 2. top函数获取的就是栈中最后一个元素
// 3. min函数获取就是栈中元素的最小值,可以使用Math.min()方法
let stack = []
function push(node)
{
return stack.push(node)
}
function pop()
{
if(stack.length){
return stack.pop()
}
}
function top()
{
return stack[stack.length - 1]
}
function min()
{
return Math.min(...stack)
}
3. 有效括号序列
描述:给出一个仅包含字符’(‘,’)‘,’{‘,’}‘,’[‘和’]',的字符串,判断给出的字符串是否是合法的括号序列,括号必须以正确的顺序关闭,"()“和”()[]{}“都是合法的括号序列,但”(]“和”([)]"不合法。
数据范围:字符串长度 0 <= n <= 10000
要求:空间复杂度O(n),时间复杂度O(n)
示例1
输入:“[”
返回值:false
示例2
输入:“[]”
返回值:true
// 思路:
// 1. 先判断字符串的长度是不是偶数,如果是奇数则一定匹配不成功直接返回false
// 2. 如果长度是偶数,定义一个空栈,从左往右遍历字符串,遇到左字符串则放进栈中
// 3. 继续遍历如果遇到右字符串立刻从栈中弹出一个字符串,如果二者不能匹配则返回false
// 4. 遍历结束后如果栈的长度为零则说明匹配成功,是有效括号序列,返回true
function isValid( s ) {
const len = s.length % 2
let stack = []
if(len) return false
for(let i of s){
if(i=='(' || i=='[' || i=='{'){
stack.push(i)
}else{
if(stack.length){
if(i==')'){
if(stack.pop() != '(') return false
}else if(i==']'){
if(stack.pop() != '[') return false
}else{
if(stack.pop() !='{') return false
}
}else{
// 说明没有左括号,肯定匹配不成功
return false
}
}
}
return !stack.length
}
4. 滑动窗口的最大值
描述:给定一个长度为 n 的数组 num 和滑动窗口的大小 size ,找出所有滑动窗口里数值的最大值。
例如给定数组[1,2,3],窗口大小为2。则所有滑动的结果可能为[1,2],[2,3]所以对应的最大值分别为[2,3]
示例1
输入:[2,3,4,2,6,2,5,1],3
返回值:[4,4,6,6,6,5]
示例2
输入:[9,10,9,-7,-3,8,2,-6],5
返回值:[10,10,9,8]
示例3
输入:[1,2,3,4],5
返回值:[]
// 方法一思路:
// 1. 判断窗口长度和数组长度的大小,窗口长度为0,或者数组长度为0,或者窗口长度大于数组长度,返回空数组
// 2. 确定可能出现的滑动结果即有几组值,n = len - size + 1(n:滑动窗口值,len:数组长度,size:窗口大小)
// 3. 遍历数组,记录所有的滑动窗口,并计算出每一个窗口中的最大值
// 4. 将记录的最大值push进入一个新的栈中,最后返回这个栈
function maxInWindows( num , size ) {
if(!size || size > num.length) return []
const endValue = num.length - size
let maxNum = []
let stack = []
for(let i=0;i<endValue+1;i++){
for(let j=i;j<i+size;j++){
stack.push(num[j])
}
const max = Math.max(...stack)
maxNum.push(max)
stack = []
}
return maxNum
}
// 方法二思路:
// 1. 判断窗口长度和数组长度的大小,窗口长度为0,或者数组长度为0,或者窗口长度大于数组长度,返回空数组
// 2. 新建两个空栈 stack 和 maxNum 遍历数组将每一项放进 stack 中,判断 stack 的长度
// 如果 stack 的长度等于 size,此时求取 stack 中的最大值,放进 maxNum 中
// 如果 stack 的长度大于 size,此时从 stack 中删除第一个元素,此时 stack 的长度会等于 size,在求取 stack 中的最大值放进 maxNum 中
// 3. 遍历结束后返回 maxNum
function maxInWindows( num , size ){
if(!num.length || !size || size > num.length) return []
let stack = [],maxNum = []
for(let i of num){
stack.push(i)
if(stack.length > size){
stack.shift()
}
if(stack.length == size){
maxNum.push(Math.max(...stack))
}
}
return maxNum
}
5. 最小的k个数
描述:给定一个长度为 n 的可能有重复值的数组,找出其中不去重的最小的 k 个数。例如数组元素是4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4(任意顺序皆可)。
示例1
输入:[4,5,1,6,2,7,3,8],4
返回值:[1,2,3,4]
说明:返回最小的4个数即可,返回[1,3,2,4]也可以
示例2
输入:[1],0
返回值:[]
示例3
输入:[0,1,2,1,2],3
返回值:[0,1,1]
// 思路:
// 1. 将数组从小到大排序
// 2. 新建一个空栈,从排序后的数组中 shift 出前 k 个数
function GetLeastNumbers_Solution(input, k){
if(!input.length || !k) return []
let stack = []
input.sort((a,b) => a-b) // 从小到大排个序,会改变原数组
for(let i=0;i<k;i++){
stack.push(input.shift())
}
return stack
}
6. 寻找第K大的数
描述: 有一个整数数组,请你根据快速排序的思路,找出数组中第 k 大的数。给定一个整数数组 a ,同时给定它的大小n和要找的 k ,请返回第 k 大的数(包括重复的元素,不用去重),保证答案存在
示例1
输入:[1,3,5,2,2],5,3
返回值:2
示例2
输入:[10,10,9,9,8,7,5,6,4,3,4,2],12,3
返回值:9
说明:去重后的第3大是8,但本题要求包含重复的元素,不用去重,所以输出9
// 思路:
// 1. 先判断数组长度是否为零,数组长度和n,k的大小关系。如果数组长度为零,或者数组长度不等于n,或者小于k。都返回false
// 2. 将数组从大到小排列,从中取出第k个数
function findKth( a , n , K ) {
if(!a.length || a.length != n || a.length < K ) return false
a.sort((a,b) => b-a) // 从大到小排列
return a[K-1]
}
7. 寻找中位数
描述:/如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
示例1
输入:[5,2,3,4,1,6,7,0,8]
返回值:"5.00 3.50 3.00 3.50 3.00 3.50 4.00 3.50 4.00 "
说明:数据流里面不断吐出的是5,2,3…,则得到的平均数分别为5,(5+2)/2,3…
示例2
输入:[1,1,1]
返回值:"1.00 1.00 1.00 "
// 思路:
// 1. 如果是一个空数组,直接返回'',
// 2. 新建一个数组,把原数组中的头部元素逐一取出放进这个数组中。在放进之后对数组进行从小到大的排序,排序完对数组长度判断
// 如果长度是奇数,则取中间值。如果长度是偶数则取中间两个值的平均值,就是中位数
// 3. 将上面得到中位数再放进一个新的栈中
// 4. 用join(' ')的方法拼成一个字符串
// 读取数据流
function Insert(num)
{
if(!num.length) return ''
let stack1 = [],stack2 = []
for(let i=0;i<num.length;i++){
stack1.push(num[i]) // 取出num中的头部元素放进stack1中
stack1.sort((a,b)=>a-b) // 对stack1进行从小到大排序
const median = GetMedian(stack1)
stack2.push(median)
}
return stack2.join(' ')
}
// 获取当前数据流中的中位数
function GetMedian(arr){
if(arr.length % 2){
// 此时数组长度为奇数,中位数是中间的值
const index = Math.floor(arr.length / 2)
const value = arr[index]
return value.toFixed(2)
}else{
// 此时数组长度是偶数,中位数是中间两个值的平均值
const index = arr.length / 2
const value = (arr[index] + arr[index - 1]) / 2
return value.toFixed(2)
}
}
8.表达式求值
描述:请写一个整数计算器,支持加减乘三种运算和括号。
要求:空间复杂度:O(n),时间复杂度:O(n)
示例1
输入:“1+2”
返回值:3
示例2
输入:“(2*(3-4))*5”
返回值:-10
示例3
输入:“3+234-1”
返回值:26
function solve( s ) {
// write code here
return eval(s)
}
三. 哈希
1. 两数之和
描述:给出一个整型数组 numbers 和一个目标值 target,请在数组中找出两个加起来等于目标值的数的下标,返回的下标按升序排列。
要求:空间复杂度 O(n),时间复杂度 O(nlogn)
示例1
输入:[3,2,4],6
返回值:[2,3]
说明:因为 2+4=6 ,而 2的下标为2 , 4的下标为3 ,又因为 下标2 < 下标3 ,所以返回[2,3]
示例2
输入:[20,70,110,150],90
返回值:[1,2]
说明:20+70=90
function twoSum(numbers, target) {
if(!numbers.length) return false
const map = new Map()
for(let i=0; i<numbers.length; i++) {
if(map.has(target-numbers[i])) {
return [map.get(target-numbers[i]) + 1, i + 1]
}else {
map.set(numbers[i], i)
}
}
}
2. 数组中出现次数超过一半的数字
描述:给一个长度为 n 的数组,数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
要求:空间复杂度:O(1),时间复杂度 O(n)
示例1
输入:[1,2,3,2,2,2,5,4,2]
返回值:2
示例2
输入:[3,3,3,3,2,2,2]
返回值:3
示例3
输入:[1]
返回值:1
// 方法一思路:
// 1. 建立一个空对象,将数组中的每一项作为对象中的key,出现次数作为值。(利用了对象中key的唯一性)
// 2. 如果这个值第一次出现就将他的值设为1,后面再出现一次,就将这个值加上1。和数组长度的一半向下取值比较
// 3. 如果小于,继续循环;如果大于终止循环,返回当前的key
// 使用一般 for 循环
// const arr = [1,2]
function MoreThanHalfNum_Solution( numbers ) {
const len = Math.floor(numbers.length / 2 )
let obj = {}
if(numbers.length == 1){
return numbers[0]
}else{
for(let i of numbers){
if(obj[i]){
obj[i]++
if(obj[i] > len){
return i
}
}else{
obj[i] = 1
}
}
return '无解'
}
}
// console.log(MoreThanHalfNum_Solution(arr));
// 使用reduce
// const arr = [3,3,3,3,2,2,2]
function MoreThanHalfNum_Solution(numbers){
const len = Math.floor(numbers.length / 2 )
if(numbers.length == 1) return numbers[0]
const obj = numbers.reduce((preValue,curValue)=>{
preValue[curValue] = (preValue[curValue] + 1) || 1
return preValue
},{})
for(let i in obj){
if(obj[i] > len) return i
}
return '无解'
}
// console.log(MoreThanHalfNum_Solution(arr));
// // 方法二:思路
// 将数组从小到大排列,取中那个数
// 如果这个数在数组中出现次数超过了一半,则排序后中间的那个数就是要求的结果
const arr = [3,3,3,3,2,2,2]
function MoreThanHalfNum_Solution(numbers){
const len = Math.floor(numbers.length / 2 )
return numbers.sort((a,b) => a -b)[len]
}
console.log(MoreThanHalfNum_Solution(arr));
3. 数组中只出现一次的两个数字
描述:一个整型数组里除了两个数字只出现一次,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。
要求:空间复杂度 O(1),时间复杂度 O(n),输出的结果按照非降序排列
示例1
输入:[1,4,1,6]
返回值:[4,6]
说明:返回的结果中较小的数排在前面
示例2
输入:[1,2,3,3,2,9]
返回值:[1,9]
// 方法一思路:
// 1. 新建一个对象 obj 和一个数组 arr
// 2. 将数组中的每一项作为对象中的key,出现次数作为值。(利用了对象中key的唯一性)
// 3. 统计每个数字出现的次数,然后对obj里面的每一项进行判断,如果对应的值为1,则将这个键放入arr数组中
// 4. 将最后得到的arr数组按照从小到大的顺序进行排列
function FindNumsAppearOnce(nums){
let obj = {}, arr = []
for(let i of nums){
if(obj[i]){
obj[i]++
}else{
obj[i] = 1
}
}
for(let j in obj){
if(obj[j] == 1){
arr.push(+j)
}
}
return arr.sort((a,b) => a-b)
}
// 方法二思路:
// 1. 新建一个数组 arr 用于存储返回的结果
// 2. 如果这个数字在数组中只出现了一次,那么从头开始找和从尾开始找得到的应该是同一个数组下标
// 3. 所以判断indexOf() 和 lastIndexOf() 返回的下标是否相同,如果相同将这个值 push 进入 arr 中
// 4. 将得到的数组按照从小到大的顺序排列
function FindNumsAppearOnce(nums){
let arr = []
for(let i of nums){
if(nums.indexOf(i) == nums.lastIndexOf(i)){
arr.push(i)
}
}
return arr.sort((a,b) => a-b)
}
4. 缺失的第一个正整数
描述:给定一个无重复元素的整数数组nums,请你找出其中没有出现的最小的正整数
要求: 空间复杂度 O(1),时间复杂度 O(n)
示例1
输入:[1,0,2]
返回值:3
示例2
输入:[-2,3,4,1,5]
返回值:2
示例3
输入:[4,5,6,8,9]
返回值:1
// 思路:
// 1. 将数组用set转换,使用while循环,终止条件是取到数组的长度。
// 2. 使用has()判断当前值是否在set数据结构中,不在则返回这个值,在则将当前值加1
function minNumberDisappeared( nums ) {
// 会超时
// if(!nums.length) return 1
// let i = 1
// while(i <= nums.length){
// if(!nums.includes(i)){
// return i
// }else{
// i++
// }
// }
// return i
let set = new Set(nums);
let i = 1;
if(!nums.length) return 1
while(i <= nums.length){
if(!set.has(i)){
return i
}else{
i++;
}
}
return i;
}
5. 三数之和
描述:给出一个有n个元素的数组S,S中是否有元素a,b,c满足a+b+c=0?找出数组S中所有满足条件的三元组。
要求:空间复杂度:O(n2),时间复杂度 O(n2)
注意:三元组(a、b、c)中的元素必须按非降序排列。(即a≤b≤c)解集中不能包含重复的三元组。
示例1
输入:[0]
返回值:[]
示例2
输入:[-2,0,1,1,2]
返回值:[[-2,0,2],[-2,1,1]]
示例3
输入:[-10,0,10,20,-10,-40]
返回值:[[-10,-10,20],[-10,0,10]]
// 思路:
// 1. 如果数组长度小于3,直接返回空数组 []
// 1. 先将原数组按照从小到大的顺序排序
// 2. 定义一个新数组 array 用来存储满足条件的结果
// 3. 在排序后的数组中遍历,设定两个值,一个是 head = i+1,一个是tail = 数组长度 -1
// 4. 执行一个while循环,循环条件是head < tail
// 5. 对当前值,head 和 tail 指向的值做一个求和操作。对求和结果判断,如果结果为 0,则将这三个值放进一个数组中并push进 array 中同时则将 haed +1 向后移一位,tail - 1向前移动一位。
// 如果大于零则将 tail - 1,如果小于零则将 head + 1
// 6. 对循环结束后得到的 array 数组,进行二维数组的去重操作。
// 7. 二维数组去重
// (1)将里面的每一项用 JSON.stringify 变为字符串
// (2)将上述结果用 new Set() 去重,在将结果里面的每一项用 JSON.parse()反转回去
function threeSum( num ) {
let len = num.length
if(len < 3) return []
let arr = []
num.sort((a,b) => a -b)
for(let i=0;i<len - 2;i++){
let head = i + 1, tail = len - 1
while(head < tail){
let sum = num[i] + num[head] + num[tail]
if(sum > 0){
tail--
}else if(sum < 0){
head++
}else{
arr.push([num[i], num[head], num[tail]])
head++
tail--
}
}
}
// 对 array 数组,进行二维数组的去重操作
let stringArr = arr.map(item => JSON.stringify(item))
let setArr = [...new Set(stringArr)]
let resultArr = setArr.map(ele => JSON.parse(ele))
return resultArr
}
console.log(threeSum([-2,0,1,1,2]));
四. 链表
1. 反转链表
描述:给定一个单链表的头结点pHead(该头节点是有值的,比如它的val是1),长度为n,反转该链表后,返回新链表。
示例1
输入:{1,2,3}
返回值:{3,2,1}
示例2
输入:{}
返回值:{}
说明:空链表则输出空
// 思路:
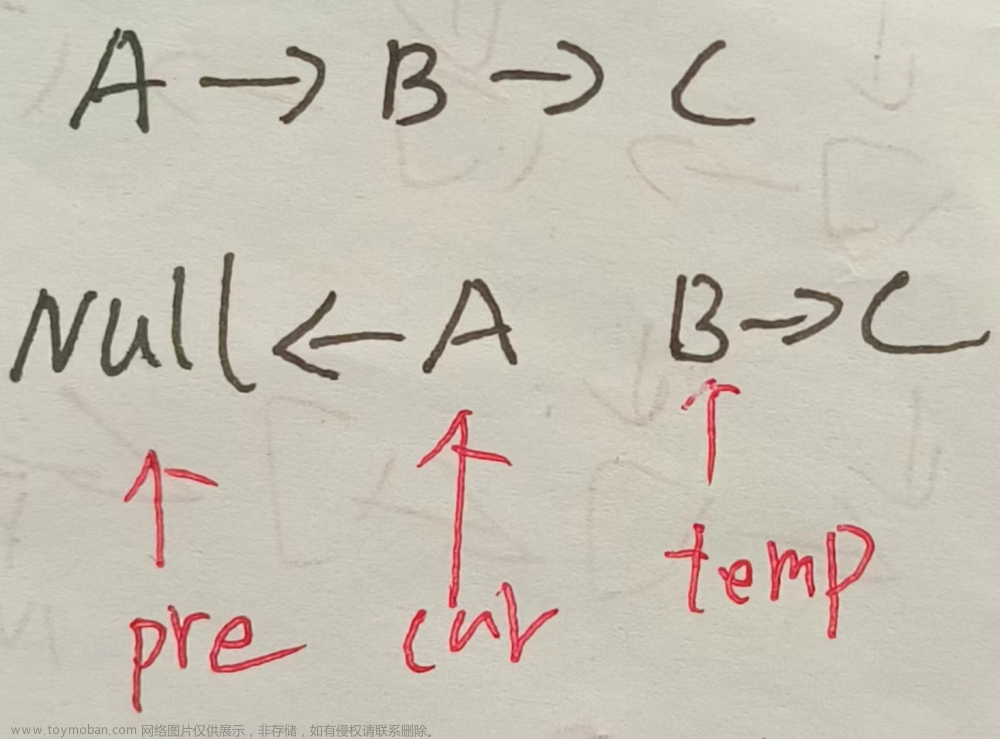
// 1. 定义两个指针,一个 pre 指向 null,一个 cur 指向当前表头
// 2. 将cur.next存起来,因为是单链表,不保存的话,改变方向之后就找不到旧节点的下个节点了
// 3. 直接改变链表方向,将cur.next 指向 pre。
// 4. 将 pre 和 cur 逐渐向后面移动,直到 cur 指向 null,此时返回 pre
function ReverseList( head ) {
// write code here
let pre = null
let cur = head
while(cur){
let temp = cur.next
cur.next = pre
pre = cur
cur = temp
}
return pre
}
2. 指定区域内的反转
五. 二叉树
1. 二叉树的前、中、后遍历
// 一. 前序遍历:根左右
// 描述:给你二叉树的根节点 root ,返回它节点值的 前序 遍历。
// 输入:{1,#,2,3}
// 返回值:[1,2,3]
/*
* function TreeNode(x) {
* this.val = x;
* this.left = null;
* this.right = null;
* }
*/
// 思路:
// 1. 先判断是否为空二叉树
// 2. 递归遍历左右子树
function preorderTraversal( root ) {
let res = []
function preorder(node){
if(!node) return
res.push(node.val)
preorder(node.left)
preorder(node.right)
}
preorder(root)
return res
}
// 二. 中序遍历:左根右
// 描述:给你二叉树的根节点 root ,返回它节点值的 中序 遍历。
// 输入:{1,2,#,#,3}
// 返回值:[2,3,1]
function inorderTraversal( root ) {
let res = []
function inorder(node){
if(!node) return
inorder(node.left)
res.push(node.val)
inorder(node.right)
}
inorder(root)
return res
}
// 三. 后序遍历:左右根
// 描述:给定一个二叉树,返回他的后序遍历的序列。
// 输入:{1,#,2,3}
// 返回值:[3,2,1]
function postorderTraversal( root ) {
let res = []
function postorder(node){
if(!node) return
postorder(node.left)
postorder(node.right)
res.push(node.val)
}
postorder(root)
return res
}
2. 二叉树的层序遍历
描述:给定一个二叉树,返回该二叉树层序遍历的结果,(从左到右,一层一层地遍历)
要求: 0 <= 二叉树的结点数 <= 1500
示例1:
输入:{3,9,20,#,#,15,7}
输出:[[3], [9, 20], [15, 7]]
示例2
输入:{1,2}
返回值:[[1],[2]]
示例3
输入:{1,2,3,4,#,#,5}
返回值:[[1],[2,3],[4,5]]
// 思路:
// 1. 如果是空二叉树返回一个空数组
// 2. 新建两个数组 res = [](用来存储最终的结果),queue = [root](用来存储每一层的结果)
// 3. 当 queue 这个数组的长度不为零时候,通过while循环将每一层的数据放入 queue 中。
// 4. 将 queue 这个数组放入 res 中。对左右子树依然执行步骤三
function levelOrder( root ) {
if(!root) return []
let res = [], queue = [root]
while (queue.length) {
res.push(queue.map(node => node.val));
queue = queue.reduce((q, node) => {
node.left && q.push(node.left);
node.right && q.push(node.right);
return q;
}, []);
}
return res;
}
3. 按之字形顺序打印二叉树
描述:给定一个二叉树,返回该二叉树的之字形层序遍历,(第一层从左向右,下一层从右向左,一直这样交替)
示例1
输入:{1,2,3,#,#,4,5}
返回值:[[1],[3,2],[4,5]]
说明:如题面解释,第一层是根节点,从左到右打印结果,第二层从右到左,第三层从左到右。
示例2
输入:{8,6,10,5,7,9,11}
返回值:[[8],[10,6],[5,7,9,11]]文章来源:https://www.toymoban.com/news/detail-631066.html
示例3
输入:{1,2,3,4,5}
返回值:[[1],[3,2],[4,5]]文章来源地址https://www.toymoban.com/news/detail-631066.html
// 思路:按照层序遍历的方式,将偶数项翻转排列,层序遍历的思路见上
function Print( pRoot ) {
if(!pRoot) return []
let res = [], queue = [pRoot], floor = 1;
while(queue.length){
// 判断是奇数层还是偶数层,如果是奇数层直接放入数组中,如果是偶数层先反转一下再放进数组中
if(floor % 2 == 1){
// 奇数层
res.push(queue.map(node => node.val))
}else{
// 偶数层
res.push(queue.map(node => node.val).reverse())
}
queue = queue.reduce((q, node) => {
node.left && q.push(node.left);
node.right && q.push(node.right);
return q;
}, [])
floor++
}
return res
}
到了这里,关于数据结构与算法常见题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!