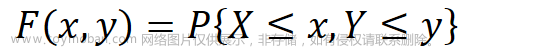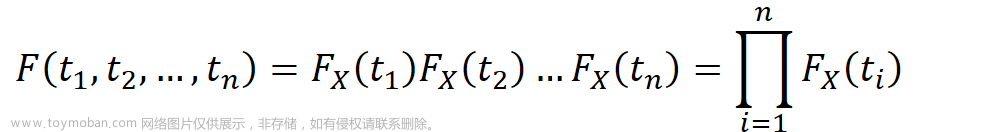本帖更新数字特征，包含期望、方差、相关系数等，要点在于记忆性质中的各种公式，遇到题目时能迅速利用已知条件计算答案。
目录
1.1离散型随机变量的数学期望
1.2连续型随机变量的数学期望
1.3随机变量函数的期望
1.4数学期望的性质
1.5条件期望
2.1方差的定义
2.2方差的性质
2.3常见离散型变量的期望与方差
2.4常见连续型变量的期望与方差
3.分布的公式总结
4.1协方差
4.2相关系数
考研数学一考纲中对这一章的要求如下：
1．理解随机变量数字特征（数学期望、方差、标准差、矩、协方差、相关系数）的概念，会运用数字特征的基本性质，并掌握常用分布的数字特征
2.会求随机变量函数的数学期望.
1.1离散型随机变量的数学期望
- 所谓的数学期望，就是均值
- 期望也可以理解为一种加权平均，而中学和小学接触的平均数是权值相同的加权平均~
1.2连续型随机变量的数学期望
- 本质与离散型的相同，但由于取值连续要通过积分来计算~
- （要求f（x）反常积分绝对收敛）
1.3随机变量函数的期望
- 本质上还是函数的嵌套，原公式的计算方式保持一致~
- 可以先根据函数计算取值，再与对应的权重相乘；亦或先求概率，再用函数的对应关系来求~
1.4数学期望的性质
- 常数的期望就是本身
- E（c+x）=Ex+c
- E（x+/-y）=Ex+/-Ey恒成立
- E(xy)=Ex*Ey，仅在x与y独立时成立
- 随机变量的独立性再判断时需要谨慎~
1.5条件期望
- 还是老套路，1个变量取某值的情况下，另一个变量的期望~
- 条件期望具有期望的一切性质~
2.1方差的定义
- 意义是衡量样本与期望的偏离程度、起伏程度~
- 标准差事方差开根号，引入的意义的是为了避免量纲的影响~
- 高中的顺口溜：样本与均值之差的平方的和的平均值~
- 但是高中学的，本质上是权值相同的样本，大学学的无论是离散型还是连续型都引入了概率的定义~
- 常用公式：Dx=E(x^2)-(Ex)^2
2.2方差的性质
- 常数的方差为0（不存在偏离）
- 若x与y独立，D(x+/-y)=Dx+Dy
- Dx=0的充要条件是：P（x=Ex）=1——x为均值的概率为1，即恒为平均值
- 标准化：(x-Ex)/标准差——期望为0，方差为1（类别标准正态分布）
2.3常见离散型变量的期望与方差
笔记中详细总结，一定要背的滚瓜烂熟~
2.4常见连续型变量的期望与方差
笔记中详细总结，一定要背的滚瓜烂熟~
3.分布的公式总结
本质就是2.3+2.4的总结，说实话，直接被结果就行，证明过程忽略吧，要求别太高~
4.1协方差
- 定义为E(xy)-Ex*Ey，即为乘积的期望减去期望的乘积~
- X与Y独立时，E（XY）=EX*EY，协方差为0，即完全不相关
- 随机变量与任何常数都独立
- 协方差的标准化，不再受量纲影响，本质为相关系数
4.2相关系数
- 协方差除以标准差的积，即为相关系数
- X与Y不相关和XY独立是两个概念
- 期望为一阶原点矩，方差为二阶中心距~
文章来源：https://www.toymoban.com/news/detail-631803.html
文章来源地址https://www.toymoban.com/news/detail-631803.html
到了这里，关于宋浩概率论笔记（四）数字特征的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
