并查集维护额外信息，算法思路类似前缀和，结构类似扑克接龙-Toy模板网

这篇具有很好参考价值的文章主要介绍了并查集维护额外信息，算法思路类似前缀和，结构类似扑克接龙。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、链接

240. 食物链

二、题目

动物王国中有三类动物 A,B,CA,B,C，这三类动物的食物链构成了有趣的环形。

AA 吃 BB，BB 吃 CC，CC 吃 AA。

现有 NN 个动物，以 1∼N1∼N 编号。

每个动物都是 A,B,CA,B,C 中的一种，但是我们并不知道它到底是哪一种。

有人用两种说法对这 NN 个动物所构成的食物链关系进行描述：

第一种说法是 1 X Y，表示 XX 和 YY 是同类。

第二种说法是 2 X Y，表示 XX 吃 YY。

此人对 NN 个动物，用上述两种说法，一句接一句地说出 KK 句话，这 KK 句话有的是真的，有的是假的。

当一句话满足下列三条之一时，这句话就是假话，否则就是真话。

当前的话与前面的某些真的话冲突，就是假话；
当前的话中 XX 或 YY 比 NN 大，就是假话；
当前的话表示 XX 吃 XX，就是假话。

你的任务是根据给定的 NN 和 KK 句话，输出假话的总数。

输入格式

第一行是两个整数 NN 和 KK，以一个空格分隔。

以下 KK 行每行是三个正整数 D，X，YD，X，Y，两数之间用一个空格隔开，其中 DD 表示说法的种类。

若 D=1D=1，则表示 XX 和 YY 是同类。

若 D=2D=2，则表示 XX 吃 YY。

输出格式

只有一个整数，表示假话的数目。

数据范围

1≤N≤500001≤N≤50000,
0≤K≤1000000≤K≤100000

输入样例：

输出样例：

三、题意

总共有三种生物，构成一个吃与被吃的闭环，给出多个描述，判断假话的个数并输出

四、代码

#include<iostream>

using namespace std;

const int N=50000+10;

int p[N],d[N];

int find(int x)
{
    if(p[x]!=x)
    {
        int t=find(p[x]);
        d[x]+=d[p[x]];
        p[x]=t;
    }
    
    return p[x];
}

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    
    for(int i=1;i<=n;i++)
    {
        p[i]=i;
    }
    
    int res=0;
    
    while(m--)
    {
        int t,x,y;
        
        scanf("%d%d%d",&t,&x,&y);
        
        if(x>n||y>n)
        {
            res++;
        }
        else
        {
            int px=find(x),py=find(y);
            if(t==1)
            {
                if(px==py&&(d[x]-d[y])%3)
                {
                    res++;
                }
                else if(px!=py)
                {
                    p[px]=py;
                    d[px]=d[y]-d[x];
                }
            }
            else
            {
                if(px==py&&(d[x]-d[y]-1)%3)
                {
                    res++;
                }
                else if(px!=py)
                {
                    p[px]=py;
                    d[px]=d[y]-d[x]+1;
                }
            }
        }
    }
    
    printf("%d\n",res);
    
    return 0;
}

五、总结

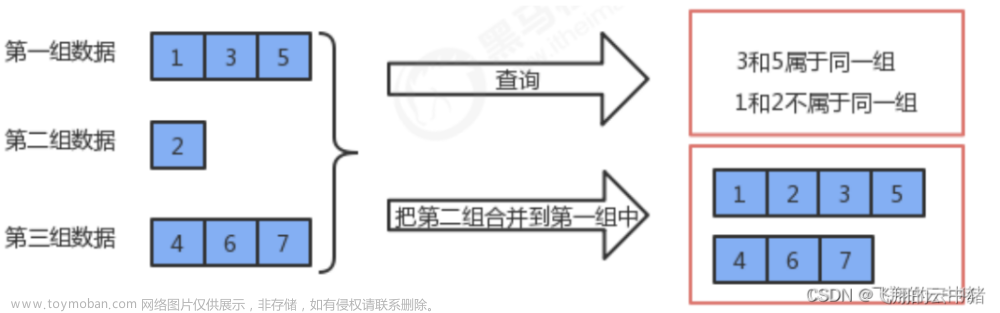
1.首先我为什么说这里使用并查集和前缀和的思路类似呢，因为我们在这里使用一个类似预处理的操作，把每一个结点到根节点的距离计算了出来，然后判断这两个节点的距离即可，前缀和是预处理前面的和，然后对两个点的和进行差运算，感觉是差不多的。

2.我们除了合并属于不同集合的元素，还需要维护一些额外的信息，比如说每一个节点到根节点的距离，怎么表示两个元素之间的关系呢，可以看它与根节点之间的距离。

3.先给出一个并查集的模板：并查集模板-两个操作：合并集合和查询两个元素是否属于同一个集合

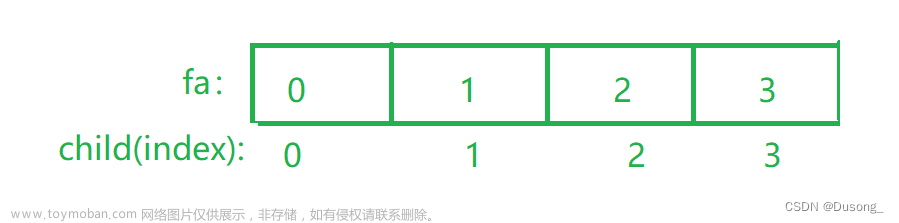
4.还是有一个问题，就是我们改变一个变量的时候要注意，是否之前对他进行了修改，修改之后我们这样写会报错，所以最好是先把需要使用的变量用一个临时变量存下来，就是这里的几行代码需要注意给这个问题

int t=find(p[x]);
d[x]+=d[p[x]];
p[x]=t;

如果先改变根节点，根节点重合，原来元素到根节点的距离就会发生变化，但是我们需要之前元素到修改之前根节点的距离，所以需要先把根节点拿出来保存，先修改结点到根节点的距离，再修改根节点

总结就是遇到类似的问题，最好就是把变量拿出来，防止修改之后发生变化，出现错误

5.这个题目需要进行的条件判断比较多：首先是正常的初始化，就是并查集的简单初始化，需要注意的是最开始每一个元素自己相当于根节点，到根节点的距离是0，定义为全局变量，不需要进行初始化。

6.如果第二个或者第三个输入的元素大于输入的总数n，那么就要把假话数字增加一，除去这种情况，再开始讨论别的情况

7.如果是表示的两个属于同类，需要进行两个判断，第一个判断是这两个动物是不是属于同一个集合（并查集的特性），如果属于同一个集合并且两个动物（或者说结点）不是同一类物种（到根节点之间的距离对3进行取模之后的数值不相等），就说明不是真话，res++;如果不属于同一个集合，说明两个元素的集合不是同一个集合，就需要把两个元素合并到同一个集合里面，还需要更新里面结点到根节点的距离，因为根节点发生了变化。在最开始条件判断之前，先把输入的第二个数，第三个数的根节点拿了出来，存在px,py里面，现在更新的话，其实不用太考虑顺序，直接更新结点和距离就可以。更新节点使用这一行代码

p[px]=py;

更新距离需要思考一下，原来结点到根节点的距离是d[x]，另一个结点到它的根节点的距离是d[y]，我们现在把x的根节点指向了y的根节点，现在y的根节点变成了总的根节点，x和y属于同类，那么他们两个元素到根节点的距离取模之后是相等的，现在x到根节点的距离是d[x]+d[px]，d[px]表示的是x的根节点到现在新的根节点的距离，d[x]+d[px]-d[y]取模之后的结果应该是等于0，所以把距离更新的代码就是这样写

d[px]=d[y]-d[x];

8.另外一种情况是x吃y：并查集里面的树状结构有点像扑克接龙游戏，只能是固定的顺序，一层可以有很多同类的，但是新的不同类的必须在下一层，假设根节点是A，然后B吃A，是第一层，C吃B，是第二层，D和A同类，排在第三层，可以吃C，也可以被B吃，如果再来一个A的同类，这个时候还是排在第三层，如果是x吃y，x假设紧靠着y的话，是排在y的下一层，取模来看的话，是模3之后比y到根节点的距离模3之后大1。分两种情况，第一种情况，x和y在一个并查集里面，并且这两个节点的到根节点的距离的差减去1对3取模(d[x]-d[y]-1)%3不等于0，表示这两个元素不符合x吃y，说明是假话，就把答案增加1。第二种情况是，两个元素不属于同一个并查集，就需要更新根节点和距离，因为在最开始的时候，把两个元素的根节点取出来存在临时变量px,py中，现在操作只需要把根节点更新，把距离更新就行，顺序不需要考虑，更新之后d[x]==d[px]+d[x],应该还是要满足(d[x]-d[y]-1)%3==0,d[px]+d[x]-d[y]-1=0,所以d[px]=d[y]+1-d[x];

9.最后输出答案即可

10.这个题目还是蛮复杂的，抽象的来理解还是比较简单，但是具体构建这个模型，讲述清楚还是比较难，也有可能是我太弱了（肯定是的哈哈）。树状结构真的抽象！简单的来说就是并查集+维护一个到根节点的距离，维护距离的时候注意根节点会发生变化，最好把根节点用临时变量先存起来，再更新根节点和距离