时序预测 | MATLAB实现BO-LSTM贝叶斯优化长短期记忆神经网络时间序列预测-Toy模板网

这篇具有很好参考价值的文章主要介绍了时序预测 | MATLAB实现BO-LSTM贝叶斯优化长短期记忆神经网络时间序列预测。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

时序预测 | MATLAB实现BO-LSTM贝叶斯优化长短期记忆神经网络时间序列预测

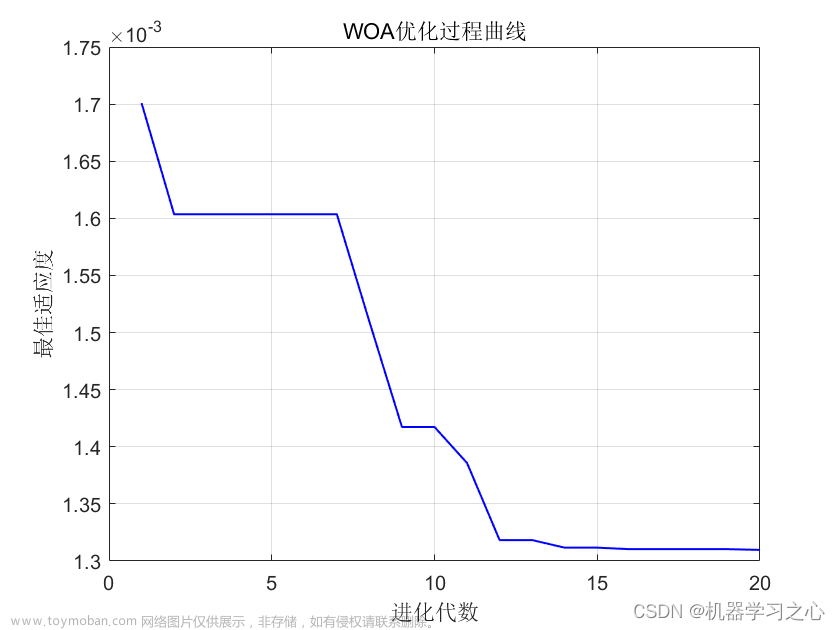
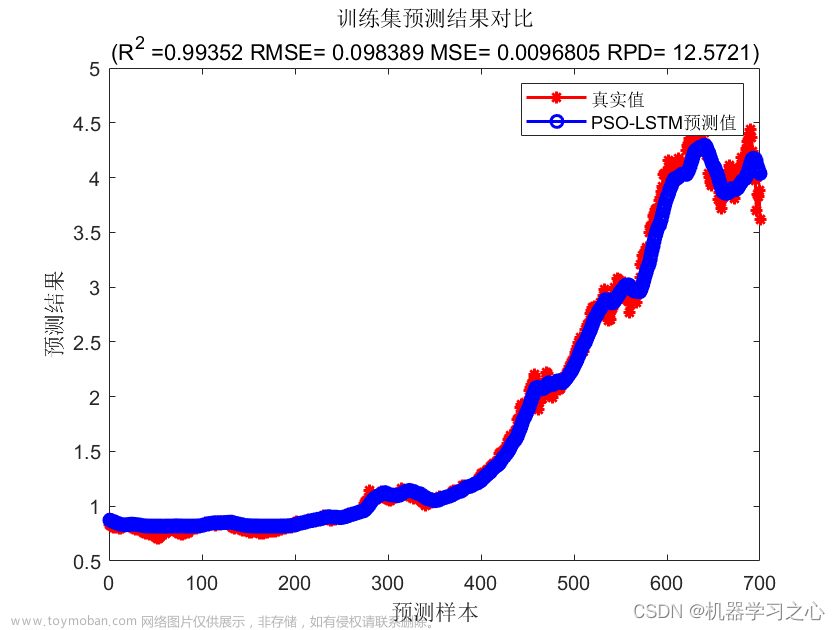
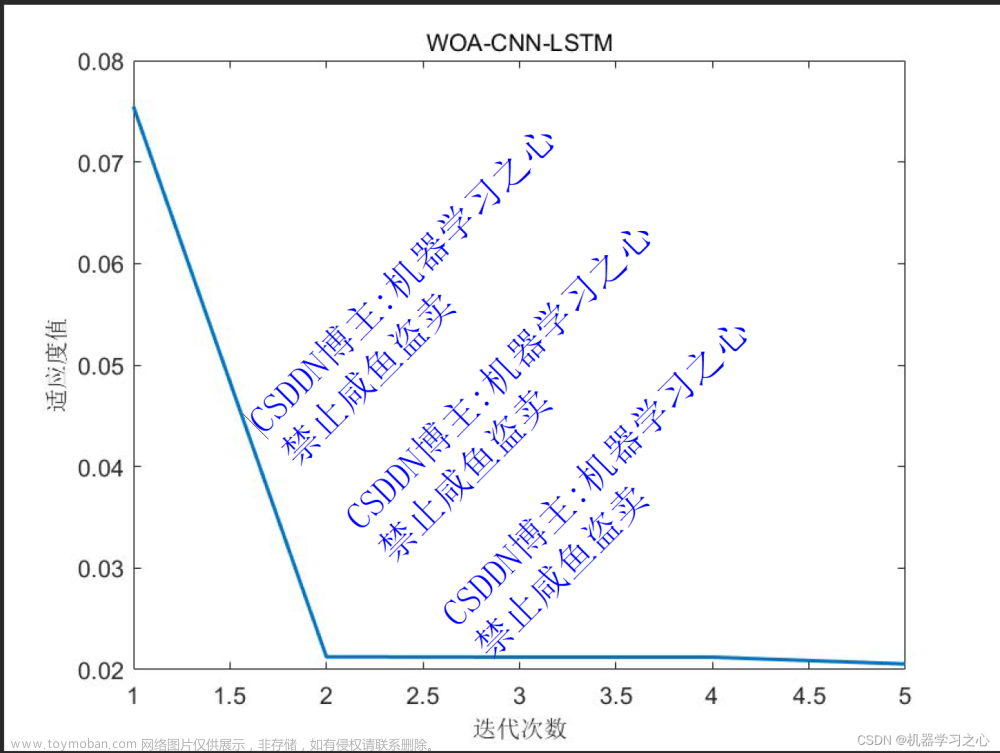
效果一览

时序预测 | MATLAB实现BO-LSTM贝叶斯优化长短期记忆神经网络时间序列预测,时间序列,BO-LSTM,贝叶斯优化长短期记忆神经网络,时间序列预测,LSTM,贝叶斯优化

基本介绍

MATLAB实现BO-LSTM贝叶斯优化长短期记忆神经网络时间序列预测。基于贝叶斯(bayes)优化长短期记忆神经网络的时间序列预测，BO-LSTM/Bayes-LSTM时间序列预测模型。
1.优化参数为：学习率，隐含层节点，正则化参数。
2.评价指标包括:R2、MAE、MSE、RMSE和MAPE等。
3.运行环境matlab2018b及以上。

模型搭建

贝叶斯优化是一种通过迭代优化来提高模型性能的方法，它可以用于优化神经网络的超参数选择。而长短期记忆神经网络（Long Short-Term Memory，LSTM）是一种适用于处理时间序列数据的循环神经网络（Recurrent Neural Network，RNN）架构。
在时间序列预测中，可以将贝叶斯优化用于调整LSTM模型的超参数，以获得更好的预测结果。以下是使用贝叶斯优化调整LSTM模型的步骤：

定义LSTM模型的目标函数：首先，需要定义一个目标函数，它接受LSTM模型的超参数作为输入，并返回一个评估指标，如均方根误差（Root Mean Squared Error，RMSE）或平均绝对误差（Mean Absolute Error，MAE）。
定义超参数空间：确定需要优化的LSTM模型的超参数以及它们的取值范围。例如，超参数可以包括LSTM的学习率，隐含层节点，正则化参数等。
运行贝叶斯优化：使用贝叶斯优化算法（如高斯过程）在定义的超参数空间中进行迭代优化。每次迭代时，根据目标函数的评估结果选择下一个要探索的超参数组合。
训练和评估LSTM模型：使用每个超参数组合训练一个LSTM模型，并在验证集上评估其性能。根据目标函数的评估结果确定最佳的超参数组合。
模型选择和预测：选择具有最佳性能的LSTM模型，并使用该模型进行时间序列的预测。

需要注意的是，贝叶斯优化是一种计算密集型的方法，因为它需要在超参数空间中进行多次模型训练和评估。因此，在实际应用中，可能需要权衡计算资源和模型性能之间的关系。
总结来说，贝叶斯优化可以用于调整LSTM模型的超参数，帮助提高时间序列预测的性能。通过迭代优化超参数，可以找到最佳的超参数组合，从而改善预测结果。

伪代码
通过调整优化算法调整模型参数，学习重复率和贝叶斯优化超参数来调整模型参数。

程序设计

完整程序和数据获取方式1：私信博主回复MATLAB实现BO-LSTM贝叶斯优化长短期记忆神经网络时间序列预测，同等价值程序兑换；
完整程序和数据下载方式2(资源处直接下载)：MATLAB实现BO-LSTM贝叶斯优化长短期记忆神经网络时间序列预测；
完整程序和数据下载方式3(订阅《LSTM长短期记忆神经网络》专栏，同时可阅读《LSTM长短期记忆神经网络》专栏内容，数据订阅后私信我获取)：MATLAB实现BO-LSTM贝叶斯优化长短期记忆神经网络时间序列预测，专栏外只能获取该程序。

%%  优化算法参数设置
%参数取值上界(学习率，隐藏层节点，正则化系数)
%%  贝叶斯优化参数范围
optimVars = [
    optimizableVariable('NumOfUnits', [10, 50], 'Type', 'integer')
    optimizableVariable('InitialLearnRate', [1e-3, 1], 'Transform', 'log')
    optimizableVariable('L2Regularization', [1e-10, 1e-2], 'Transform', 'log')];

%% 创建混合LSTM网络架构
% 输入特征维度
numFeatures  = f_;
% 输出特征维度
numResponses = 1;
FiltZise = 10;
%  创建"LSTM"模型
    layers = [...
        % 输入特征
        sequenceInputLayer([numFeatures 1 1],'Name','input')
        sequenceFoldingLayer('Name','fold')
        % LSTM特征学习
        lstmLayer(50,'Name','lstm1','RecurrentWeightsInitializer','He','InputWeightsInitializer','He')
        % LSTM输出
        lstmLayer(optVars.NumOfUnits,'OutputMode',"last",'Name','bil4','RecurrentWeightsInitializer','He','InputWeightsInitializer','He')
        dropoutLayer(0.25,'Name','drop3')
        % 全连接层
        fullyConnectedLayer(numResponses,'Name','fc')
        regressionLayer('Name','output')    ];

    layers = layerGraph(layers);
    layers = connectLayers(layers,'fold/miniBatchSize','unfold/miniBatchSize');

%% LSTM训练选项
% 批处理样本
MiniBatchSize =128;
% 最大迭代次数
MaxEpochs = 500;
    options = trainingOptions( 'adam', ...
        'MaxEpochs',500, ...
        'GradientThreshold',1, ...
        'InitialLearnRate',optVars.InitialLearnRate, ...
        'LearnRateSchedule','piecewise', ...
        'LearnRateDropPeriod',400, ...
        'LearnRateDropFactor',0.2, ...
        'L2Regularization',optVars.L2Regularization,...
        'Verbose',false, ...
        'Plots','none');

%% 训练混合网络
net = trainNetwork(XrTrain,YrTrain,layers,options);

参考资料

[1] https://blog.csdn.net/kjm13182345320/article/details/129036772?spm=1001.2014.3001.5502
[2] https://blog.csdn.net/kjm13182345320/article/details/128690229文章来源地址https://www.toymoban.com/news/detail-632761.html

到了这里，关于时序预测 | MATLAB实现BO-LSTM贝叶斯优化长短期记忆神经网络时间序列预测的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！