图论＜最短路问题＞模板-Toy模板网

这篇具有很好参考价值的文章主要介绍了图论＜最短路问题＞模板。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

图论 <最短路问题>

有向图

1.邻接矩阵，稠密图

2.邻接表（常用）单链表，每一个点都有一个单链表，插入一般在头的地方插，

图的邻接表的存储方式

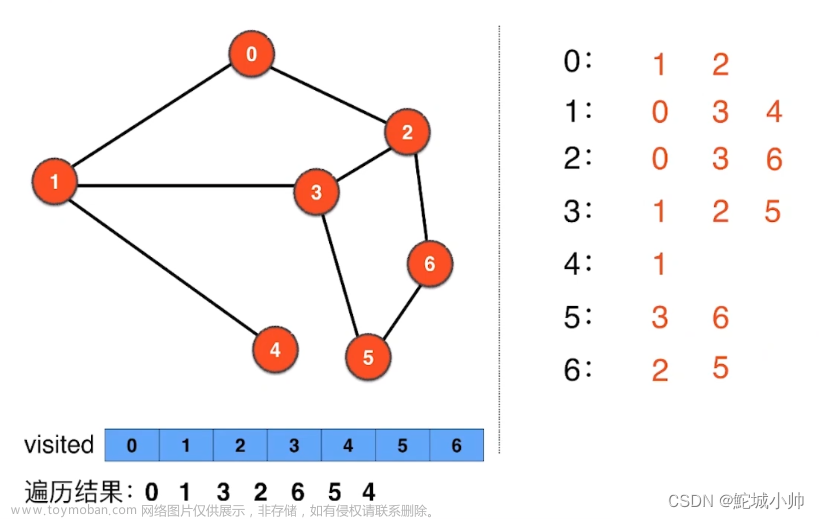
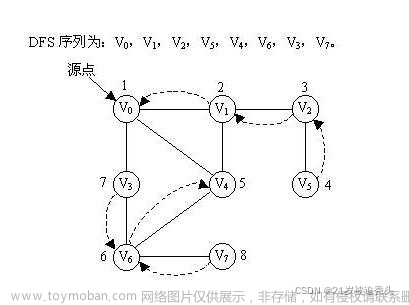
树的深度优先遍历

特殊的深度优先搜索，难点是如何实现，一条道走到黑

const int N=100010,M=n*2;
int h[N],e[N],ne[N],idx;
bool st[N];//记录状态

void add(int a,int b)
{
	e[idx]=b;
	ne[idx]=h[a];
	h[a]=idx++;
}
void dfs(int u)
{
	st[u]=true;
	for(i=h[u];i!=-1;i=ne[i])
	{
		int j=e[i];//当前节点对应的图的值；
		if(!st[j])dfs(j);
	}
}
int main()
{
	memset(h,-1,sizeof(h));
	
	return 0;
}

树的宽度优先遍历

例题：图的层序搜索

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
using namespace std;

const int N=100010;
int n,m;
int d[N];
int e[N],h[N],idx,ne[N];
void add(int a,int b)
{
	e[idx]=b;
	ne[idx]=h[a];
    h[a]=idx++;
}
void bfs()
{memset(d,-1,sizeof d);
	queue<int> q;
	d[1]=0;
	q.push(1);
	while(q.size())
	{
		auto t=q.front();
		q.pop();
		for(int i=h[t];i!=-1;i=ne[i])
		{
			int j=e[i];
			if(d[j]==-1)
			{
				d[j]=d[t]+1;
				q.push(j);
			}
		}
	}
	printf("%d",d[n]);
}
int main()
{
	cin>>n>>m;
	memset(h,-1,sizeof h);
	for(int i=0;i<m;i++)
	{
		int a,b;
		cin>>a>>b;
		add(a,b);
	}
	bfs();
	
	return 0;
}

拓扑序列（有向图）

例题：有向图的拓扑序列文章来源地址https://www.toymoban.com/news/detail-633037.html

#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;

int n, m;
int h[N], e[N], ne[N], idx;
int d[N];
int q[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool topsort()
{
    int hh = 0, tt = -1;

    for (int i = 1; i <= n; i ++ )
        if (!d[i])
            q[ ++ tt] = i;

    while (hh <= tt)
    {
        int t = q[hh ++ ];

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (-- d[j] == 0)
                q[ ++ tt] = j;
        }
    }

    return tt == n - 1;
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    for (int i = 0; i < m; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);

        d[b] ++ ;
    }

    if (!topsort()) puts("-1");
    else
    {
        for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);
        puts("");
    }

    return 0;
}

迪杰斯特拉算法(朴素版)

#include<cstdio>
#include<algorithm>
#include<iostream>
#include<cstring>
using namespace std;
const int a1=510;
int n,m;
int g[a1][a1];
int dist[a1];
bool st[a1];
int dijk()
{
	memset(dist,0x3f,sizeof dist);
	dist[1]=0;
	for(int i=0;i<n-1;i++)
	{
		int t=-1;
		for(int j=1;j<=n;j++)
		{
			if(!st[j]&&(t==-1||dist[t]>dist[j]))t=j;
		}
		for(int j=1;j<=n;j++)
		dist[j]=min(dist[j],dist[t]+g[t][j]);
		
		st[t]=true;
	}
	if(dist[n]==0x3f3f3f3f)return -1;
	return dist[n];
}
int main()
{
	cin>>n>>m;
	memset(g,0x3f,sizeof g);
	while(m--)
	{
		int a,b,c;
		cin>>a>>b>>c;
		g[a][b]=min(g[a][b],c);
	}
	cout<<dijk();
	return 0;
}

迪杰斯特拉算法（堆优化版）

#include<iostream>
#include<queue>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
typedef pair<int,int> pii;
const int N =1e6 + 10;
int n,m,a,b,c;
int h[N],e[N],ne[N],w[N],idx;
int dist[N];
bool st[N];
void add(int a,int b,int c)
{
	e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
int dijk()
{
	memset(dist,0x3f3f3f3f,sizeof dist);
	dist[1]=0;
	priority_queue<pii, vector<pii>, greater<pii>> heap;
	heap.push({0,1});
	while(heap.size())
	{
		auto t=heap.top();
		heap.pop();
		int ver=t.second,distance=t.first;
		if(st[ver])continue;
		st[ver]=true;
		for(int i=h[ver];i!=-1;i=ne[i])
		{
			int j=e[i];
			if(dist[j]>dist[ver]+w[i])
			{
				dist[j]=dist[ver]+w[i];
				heap.push({dist[j],j});
			}
		}
	}
	if(dist[n]==0x3f3f3f3f)return -1;
	return dist[n];
}
int main()
{
	cin>>n>>m;
	memset(h,-1,sizeof h);
	while(m--)
	{
		cin>>a>>b>>c;
	    add(a,b,c);
	}
	cout<<dijk();
	return 0;
}

到了这里，关于图论＜最短路问题＞模板的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！