[图论第三节]最小生成树/二分图-Toy模板网

这篇具有很好参考价值的文章主要介绍了[图论第三节]最小生成树/二分图。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

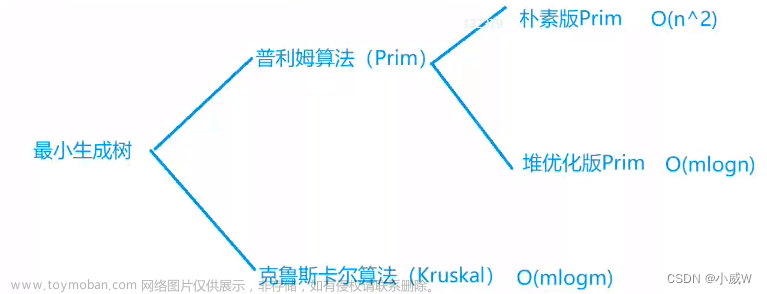
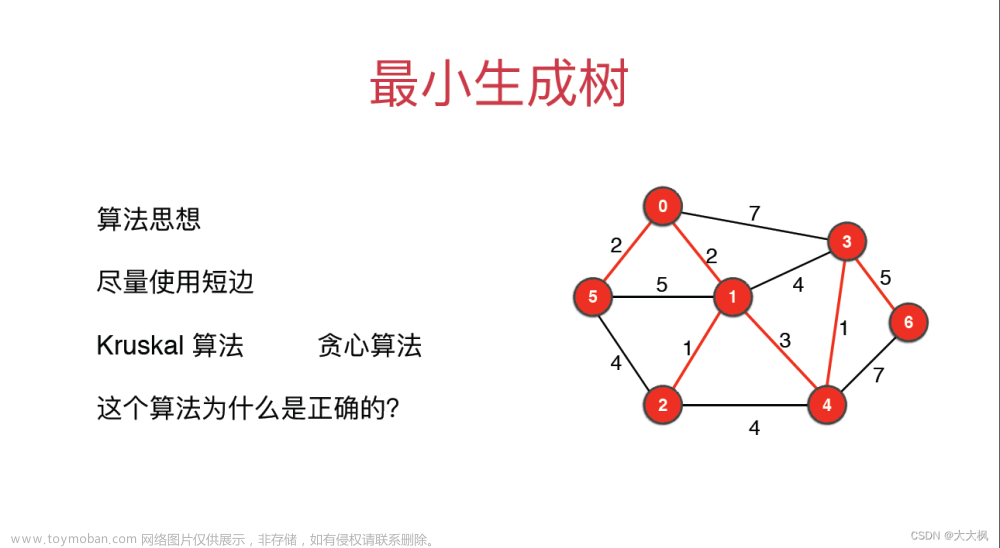
最小生成树

Prim算法

朴素版Prim O(n^2)

稠密图
步骤：
- S：表示最小生成树的集合
- 初始化距离
- 找距离集合S最近的节点
- 将节点加入集合S
- 用该节点更新非S点到集合S点的距离

代码：

const int N = 510;
const int INF = 0x3f3f3f3f;
int g[N][N];
int d[N];//非生成树节点与生成树节点的最短距离
int st[N];
int n, m;

int prim(){
    memset(d, 0x3f, sizeof d);//初始化
    
    int res = 0;//记录生成树权值和
    
    for(int i = 0; i < n; ++ i){//遍历n次选取n个点加入生成树
        
        int t = 0;
        for(int j = 1; j <= n; ++ j){
            if(!st[j] && (!t || d[j] < d[t]))//在非生成树集合中选取最小距离的点
                t = j;
        }
        st[t] = 1;//加入生成树集合
        
        if(i && d[t] == INF) return INF;//某个点与生成树集合不联通，则不存在生成树
        if(i) res += d[t]; //累加最小权值
        
        for(int j = 1; j <= n; ++ j) //更新其他点到生成树的距离
            d[j] = min(d[j], g[t][j]);
    }
    
    return res;
    
}
int main(){
    cin >> n >> m;
    
    memset(g, 0x3f, sizeof g);
    
    while(m -- ){
        int u, v, w;
        cin >> u >> v >> w;
        g[u][v] = g[v][u] = min(g[u][v], w);//无向图去重边
    }
    
    int t = prim();
    if(t == INF) cout << "impossible";
    else cout << t;
    return 0;
}

堆优化版Prim O(mlogn)
- 用堆优化找最短距离的过程将O(n)-->O(1)

Kruskal算法 O(mlogm)

稀疏图
步骤：
- 将所有边的权值从小到大排序
- 枚举每条边u--v, w
- 若u，v不同时在生成树集合中，那么将这条边加入集合
- 利用并查集

代码：

const int N = 2e5 + 10;
const int INF = 0x3f3f3f3f;
int f[N];
struct edge{
    int u, v, w;
    //运算符重载
    bool operator< (const edge &e)const{
        return w < e.w;
    }
}edges[N];

int n, m;

int find(int x){
    return x == f[x] ? x : (f[x] = find(f[x]));
}

int kruskal(){
    sort(edges + 1, edges + 1 + m);//权值排序
    
    for(int i = 1; i <= n; ++ i) f[i] = i;//并查集初始化
    
    int res = 0, cnt = 0;//res记录总权值，cnt记录边的条数
    for(int i = 1; i <= m; ++ i){//遍历每条边
        int u = edges[i].u;//获取信息
        int v = edges[i].v;
        int w = edges[i].w;
        u = find(u), v = find(v);//祖宗节点
        if(u != v){//不在同一集合中
            res += w;
            cnt ++ ;
            f[u] = v;//加入同一集合
        }
    }
    
    if(cnt < n - 1) return INF;//边数小于节点数-1，则不连通，不存在最小生成树
    else return res;
}
int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= m; ++ i){
        int a, b, c;
        cin >> a >> b >> c;
        edges[i] = {a, b, c};
    }
    
    int t = kruskal();
    if(t == INF) cout << "impossible";
    else cout << t;
    return 0;
}

二分图

判别二分图-染色法 O(m + n)

一个图是二分图当接近当图中不含有奇数（就是离散数学中的二部图）

代码：

const int N = 1e5 + 10;
const int M = 2 * N;
int h[N], e[M], ne[M], idx = 1;
int color[N];
int n, m;

void add(int u, int v){
    e[idx] = v;
    ne[idx] = h[u];
    h[u] = idx;
    idx ++ ;
}

//dfs染色，并且判断染色过程是否有矛盾
bool dfs(int u, int c){
    color[u] = c;//染色

    for(int i = h[u]; i; i = ne[i]){//遍历邻接点
        int j = e[i];
        if(!color[j]){//没有染色就染色
            if(!dfs(j, 3 - c)) return false;//染色出现矛盾
        }else if(color[j] == c) return false;//已经染色，判断相邻点是否同色
    }
    return true;
}

int main(){
    cin >> n >> m;
    while(m -- ){
        int u, v;
        cin >> u >> v;
        add(u, v);//无向图建边
        add(v, u);
    }
    
    bool flag = true;
    for(int i = 1; i <= n; ++ i){//以所有点为起点染色，因为可能不连通
        if(!color[i]){
            flag = dfs(i, 1);
            if(!flag) break;
        }
    }
    
    if(flag) cout << "Yes";
    else cout << "No";
    return 0;
}

匈牙利算法最坏O(mn)

求二分图的最大匹配数

代码：

const int N = 510;
const int M = 1e5 + 10;
int h[N], e[M], ne[M], idx = 1;
int match[N]; 
int st[N];
int n1, n2, m;

void add(int a, int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx ++ ;
}

bool find(int x){
    for(int i = h[x]; i; i = ne[i]){ //遍历该节点邻接的所有节点
        int j = e[i];
        if(!st[j]){
            st[j] = 1;//不管j有没有匹配过，强制标记为已经匹配，为了防止匹配j的节点再次将j匹配
            if(!match[j] || find(match[j])){ //j没有匹配或者匹配j的节点可以换一个匹配，在换匹配的过程中不会再匹配j，因为j已经被标记
                match[j] = x; //将x与j匹配
                return true; //成功匹配
            }
        }
    }
    return false;
}

int main(){
    cin >> n1 >> n2 >> m;
    
    while(m -- ){
        int a, b;
        cin >> a >> b;
        add(a, b); //只用一次
    }
    
    int res = 0;//记录最大匹配数
    for(int i = 1; i <= n1; ++ i){//匹配每一个节点
        memset(st, 0, sizeof st); 
        if(find(i)) res ++ ; //匹配成功
    }
    
    cout << res;
    return 0;
}