麻雀搜索算法( sparrow search algorithm,SSA) 是2020 年新提出的一种元启发式算法[1],它是受麻雀种群的觅食和反捕食行为启发,将搜索群体分为发现者、加入者和侦察者 3 部分,其相互分工寻找最优值,通过 19 个标准测试函数验证 SSA 算法在搜索精度,收敛速度,稳定性和避免局部最优值方面均优于现有算法。
麻雀搜索算法虽有以上优点,但如何调节各部分之间的控制参数,以及如何保证 3 部分之间可以较好的相互配合是一个必须考虑的问题。为解决这个问题,许多学者都进行了尝试,诸如混沌初始化、变异、混沌扰动、反向学习等方法都被引入其中,因此,本文也将尝试通过混沌初始化、变异、扰动等策略提高算法性能。
00 文章目录
1 麻雀搜索算法原理
2 自适应变异麻雀搜索算法
3 代码目录
4 算法性能
5 源码获取
6 总结
01 麻雀算法原理
感兴趣的读者可以自行搜索,这部分不再赘述
02 自适应变异麻雀搜索算法
2.1 Chebyshev 混沌映射
与其他群智能算法一样,原始 SSA 在求解复杂问题时,通过随机生成位置的方法初始化麻雀种群的个体位置,会导致种群的多样性低,对问题进行寻优的收敛速度比较慢。为了能够让麻雀个体在算法开始时有较高的全局搜索能力,需要让麻雀种群的位置均匀分布在整个问题的解空间内,因此使用混沌算子对麻雀种群进行初始化。
混沌作为一种非线性的自然现象,以其混沌序列具有遍历性、随机性等优点,被广泛用于优化搜索问题。利用混沌变量搜索显然比无序随机搜索具有更大的优越性[2]。
目前文献中常用的混沌扰动方程有Logistic映射和Tent映射等。Logistic映射在作者前面的文章中介绍过,由文献[3]可知Logistic映射的分布特点是:中间取值概率比较均匀,但在两端概率特别高,因此当全局最优点不在设计变量空间的两端时,对寻找最优点是不利的。而Tent混沌映射具有比Logistic混沌映射更好的遍历均匀性和更快的搜索速度。下图中展示了Logistic和Tent的混沌序列:

可以看到,Logistic混沌映射在边界区域取值概率明显更高,而Tent在可行域的取值概率更为均匀,因此若将Logistic混沌映射用于初始化种群时,其混沌序列的不均匀性会影响算法寻优的速度和精度。因此本文利用Tent的遍历性产生更为均匀分布的混沌序列,减少初始值对算法优化的影响。
Tent混沌映射的表达式如下:
分析Tent混沌迭代序列能够发现序列中存在小周期,并且存在不稳周期点. 为避免Tent混沌序列在迭代时落入小周期点和不稳定周期点,在原有的Tent 混沌映射表达式上引入一个随机变量rand(0, 1) /N ,则改进后的Tent混沌映射表达式如下[4]:
其中: N 是序列内粒子的个数。引入随机变量rand(0, 1) /N 不仅仍然保持了Tent混沌映射的随机性、遍历性、规律性,而且能够有效避免迭代落入小周期点和不稳定周期点内。本文算法引入的随机变量,既保持了随机性, 又将随机值控制在一定的范围之内,保证了Tent混沌 的规律性.根据Tent混沌映射的特性。改进的Tent混沌序列效果如下:
由图可知,改进后的Tent混沌映射其均匀性得到了提高,因此本文以改进Tent混沌性来代替麻雀搜索算法的随机初始化,以提高和改善初始种群在搜索空间上的分布质量,加强其全局搜索能力,从而提高算法求解精度。
2.2 趋优反向学习和混合变异扰动策略
对于迭代中的每一个麻雀个体,通过比较其适应度和平均适应度的大小关系将反向学习和混合变异扰动动态执行,增强算法的局部极值逃逸能力,改善其寻优效果。
2.2.1趋优反向学习
许多群体智能算法都采用随机算子对最优解进行扰动,这将导致收敛速度变慢。2005 年,Tizhoosh[6]提出反向学习策略(OBL)。OBL 提出对点的概念,用对立代替随机,在当前问题的解空间内寻找当前解的反向解,然后通过评估当前解和反向解的值,保留更好的解来取代原解中较差的解。因此本文对适应度较差个体执行趋优反向学习策略,提高种群质量的同时扩大算法的搜索区域,以补足算法的全局勘探能力。
首先对当前个体实施反向学习策略,得到反向个体:
其中: xlj 和 xuj 分别为第 j 维分量的下界和上界。
文献[6]指出反向个体优于当前个体的概率高于 50% ,考虑到仍有部分个体在反向学习之后个体质量有所降低,为了减少这种现象发生的概率并保持种群多样性,将求得的反向个 体和当前种群中最优个体进行凸组合,得到趋优反向个体:
其中: a为[0,1]的随机数; xgbest,j是当前种群全局最佳个体的第 j 维分量。
通过实施该策略,即使最初求得的反向个体相较于当前个体有所退化,但与当前种群中最优个体进行凸组合后,反向解还会接受一部分来自最优个体的特征,进一步提升了反向个体 的质量,同时也提高了算法的勘探能力、种群多样性和算法的收敛精度[7]。
2.2.2 混合变异算子
使用标准的柯西分布进行变异处理,可以帮助变异之后的麻雀个体迅速跳出局部极值。按照下式对当前麻雀个体进行变异:
高斯分布的点分布较为集中,该特征能够产生于原点相距较近的随机数,经过高斯变异之后的麻雀个体在位置进行很小的范围内扰动,可以提高变异个体的局部搜索能力。使用标准的高斯分布进行变异处理,按照下式对当前麻雀个体进行变异:
高斯-柯西混合变异算子通过线性权重系数将标准高斯变异得到的新麻雀个体位置和标准柯西变异得到的新麻雀个体位置生成一个全新的麻雀个体位置 Xtb_new。新麻雀个体的表达式为:
从上式可以看出,算法开始运行时,t值较小,柯西变异的权值较大,通过柯西变异获得较大步长,避免算法陷入局部最优解。随着算法不断运行,t 值较大, 高斯变异的权值较大,高斯变异杰出的局部搜索能力使得候选解在局部范围进行精确搜索,提高算法的寻优精度[8]。
2.3 发现者-加入者自适应调整策略
在 SSA算法中,发现者和加入者的数目比例保持不变,这会导致在迭代前期,发现者的数目相对较少,无法对全局进行充分的搜索,在迭代后期,发现者的数目又相对较多,此时已不需要更多的发现者进行全局搜索,而需要增加加入者的数量进行精确的局部搜索。为解决这个问题,提出发现者-加入者自适应调整策略,该策略在迭代前期,发现者可以占种群数目的多数,随着迭代次数的增加,发现者的数目自适应减少,加入者的数目自适应增加,逐步从全局搜索转为局部精确搜索,从整体上提高算法的收敛精度。发现者和加入者数目调整式为
式中:pNum 为发现者数目;sNum 为加入者数目;b为比例系数,用于控制发现者和加入者之间的数目;k为扰动偏离因子,对非线性递减值 r 进行扰动[9]。
2.4改进后的麻雀搜索算法
自适应变异麻雀搜索算法
(Adaptive Mutation-Sparrow Search optimization Algorithm, AM-SSA)流程图如下:

03 代码目录

其中,AM_SSA、SSA、PSO、GA都是可独立运行的主程序,而compare.m则可以比较不同算法的迭代曲线情况。
代码注释完整,其中部分AM_SSA程序如下:
04 算法性能
4.1 测试函数
为了能够验证自适应变异麻雀搜索算法对比粒子群算法、遗传算法以及麻雀搜索算法有更好的效果,本文选用4个CEC的标准测试函数Sphere、Griewank、Rastrigin、Rosenbrock对算法的寻优精度、跳出局部能力、全局寻优能力进行检验。4个函数的表达式如下:
4.1.1 Sphere函数
Sphere 函数的自变量𝑥𝑖的取值的范围:-100<𝑥𝑖<100;该函数存在唯一的一个全局的最小值,且当𝑥=(0,0,…,0)时,函数取得全局最小值 f1(x) = 0。选择该函数是对算法寻优的精度进行测试。
4.1.2 Griewank函数
Griewank 函数的自变量𝑥𝑖的取值的范围:-600<𝑥𝑖<600;该函数在整个的数 据分布含有大量局部极值,但是存在全局最小值 f2(x) = 0,是一种比较复杂的多模的复杂性问题,因此选择该函数目的是对算法是否跳出局部,能够继续搜索的 能力进行测试。
4.1.3 Rastrigin函数
Rastrigin 函数的自变量𝑥𝑖的取值的范围:-5.12<𝑥𝑖<5.12;在 x = ( 0,0 ,…, 0 ) 处的时候存在全局极小点 0,该函数是一个非线性的多峰值函数,存在大量的局部最小值,寻找全局极小值时有一定的困难,因此用此函数可以,对算法的全局寻优能力检验测试。
4.1.4 Rosenbrock函数
Rosenbrock 函数的自变量𝑥𝑖的取值的范围:-30<𝑥𝑖<30;该函数是一单峰函数, 存在全局极小值,位于一个类似开口向上的抛物线的最低点处,虽然能够比较容易找到,但是很难收敛到最低处,因此可以测试全局寻优的能力。
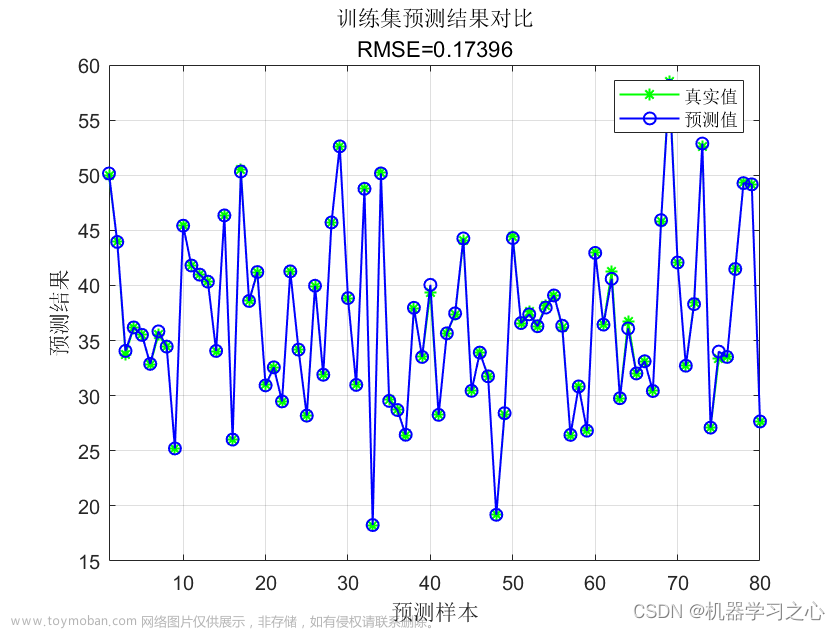
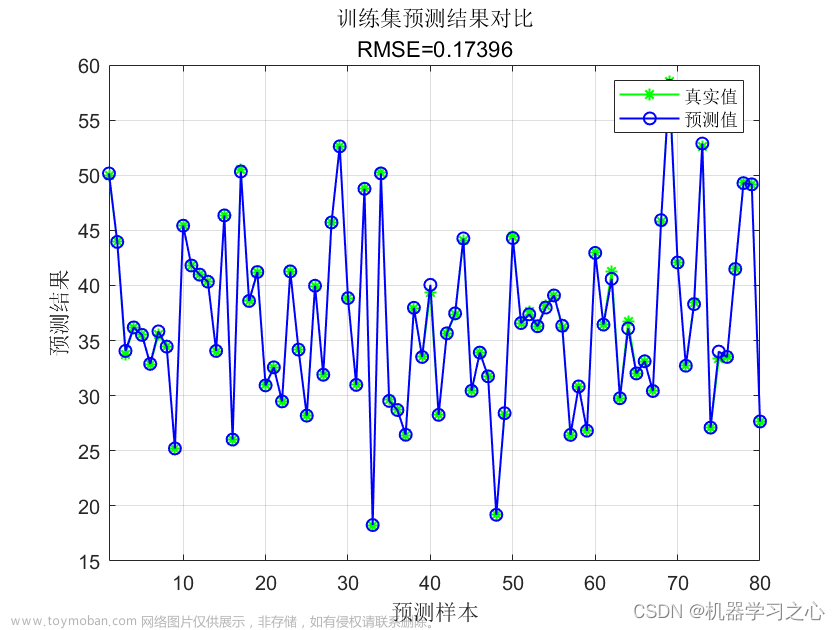
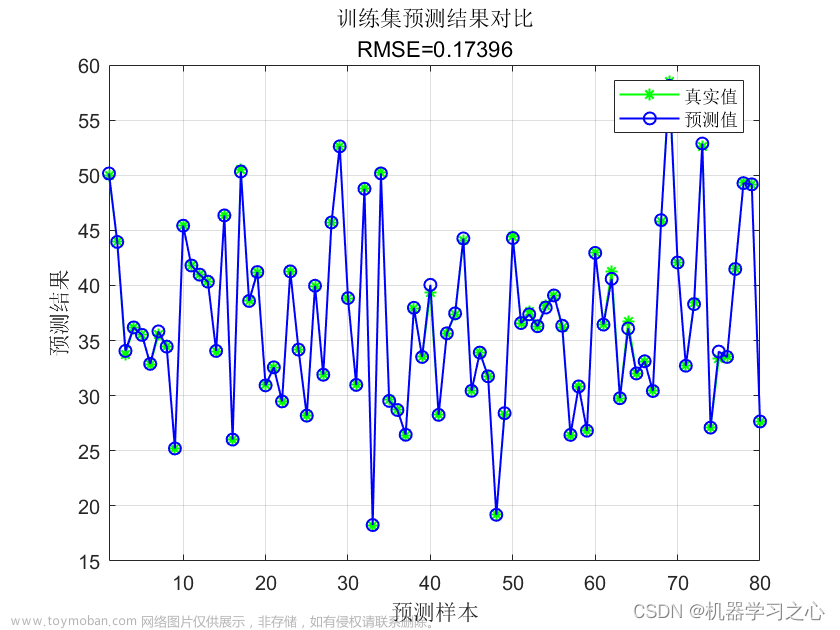
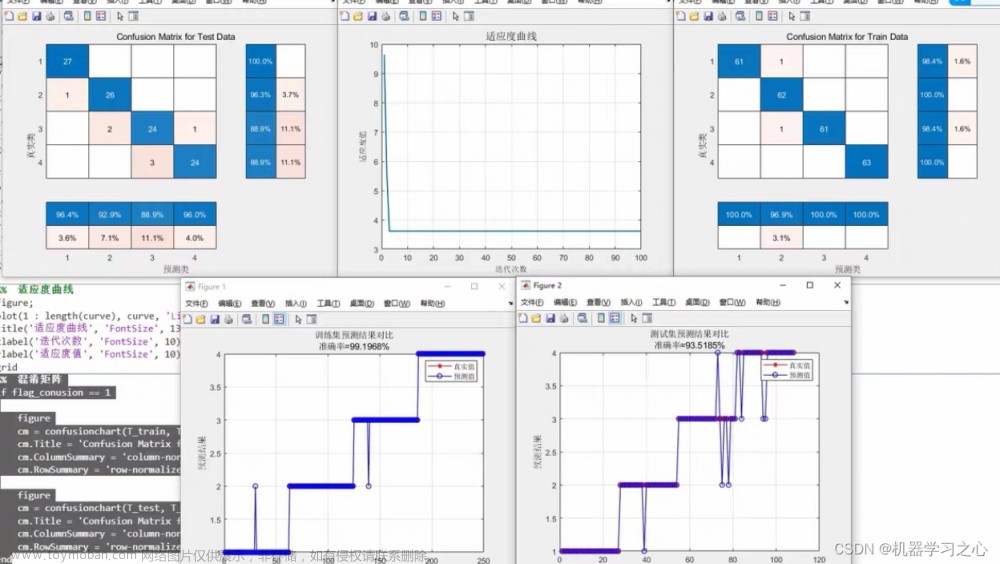
4.2 测试结果
Sphere函数
Griewank函数
Rastrigin函数
Rosenbrock函数
可以看到改进后的麻雀搜索算法后能够极大的提升其全局寻优的性能,无论是收敛速度还是精度都得到了极大的提高。这里的测试函数还是比较简单了,所以效果并没有太明显,在后面的文章中作者也会引入更复杂的测试函数来对算法性能进行验证。
05 源码获取
代码获取可关注我
06 总结
本文通过变异、混沌初始化、反向学习等策略对麻雀搜索算法进行了改进,并取得了不错的效果。对于算法的改进还可以通过混合其他智能算法来实现,后面作者也会这类方法进行更新,欢迎关注。
参考文献
[1] XUE J K, ShEN B. A novel swarm intelligence optimization approach: sparrow search algorithm [J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
[2] 张云鹏,左飞,翟正军.基于双Logistic变参数和Cheby-chev混沌映射的彩色图像密码算法[J.西北工业大学学报, 2010,28(4): 628-632.
[3] 江善和,王其申,汪巨浪.一种新型SkewTent映射的混沌混合优化算法[J.控制理论与应用, 2007,24(2): 269-273.
[4] 张娜,赵泽丹,包晓安,等.基于改进的Tent混沌万有引力搜索算法[J].控制与决策,2020,35(4):893-900.
[5] Tizhoosh H R. Opposition-based learning: a new scheme for machine intelligence[C] ∥International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06), November 28-30, 2005, Vienna, Austria. New York: IEEE Press, 2005: 695-701.
[6] Tizhoosh H R. Opposition-based learning: a new scheme for machine intelligence[C]/ /Proc of International Conference on Computational Intelligence for Modeling,Control and Automation. Piscataway,NJ: IEEE Press,2005: 695-701.
[7] 左汶鹭,高岳林.基于随机邻域变异和趋优反向学习的差分进化算法[J].计算机应用研究,2023,40(07):2003-2012.DOI:10.19734/j.issn.1001-3695.2022.11.0785.
[8] 陈深,刘以安,宋海凌.改进麻雀算法在天波雷达定位中的应用[J].激光与光电子学进展,2023,60(10):350-357.
[9]唐延强,李成海,宋亚飞等.自适应变异麻雀搜索优化算法[J].北京航空航天大学学报,2023,49(03):681-692.DOI:10.13700/j.bh.1001-5965.2021.0282.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。文章来源:https://www.toymoban.com/news/detail-634776.html
如果这篇文章对你有帮助或启发,可以点击右下角的赞 (ง •̀_•́)ง(不点也行)文章来源地址https://www.toymoban.com/news/detail-634776.html
到了这里,关于自适应变异麻雀搜索算法及其Matlab实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!