2021 年高教社杯全国大学生数学建模竞赛题目
机场的出粗车问题
大多数乘客下飞机后要去市区(或周边)的目的地,出租车是主要的交通工具之一。国内多数机场都是将送客(出发)与接客(到达)通道分开的。送客到机场的出租车司机都将会面临两个选择:
(A) 前往到达区排队等待载客返回市区。出租车必须到指定的“蓄车池”排队等候,依“先来后到”排队进场载客,等待时间长短取决于排队出租车和乘客的数量多少,需要付出一定的时间成本。
(B) 直接放空返回市区拉客。出租车司机会付出空载费用和可能损失潜在的载客收益。
在某时间段抵达的航班数量和“蓄车池”里已有的车辆数是司机可观测到的确定信息。通常司机的决策与其个人的经验判断有关,比如在某个季节与某时间段抵达航班的多少和可能乘客数量的多寡等。如果乘客在下飞机后想“打车”,就要到指定的“乘车区”排队,按先后顺序乘车。机场出租车管理人员负责“分批定量”放行出租车进入“乘车区”,同时安排一定数量的乘客上车。在实际中,还有很多影响出租车司机决策的确定和不确定因素,其关联关系各异,影响效果也不尽相同。
请你们团队结合实际情况,建立数学模型研究下列问题:
(1) 分析研究与出租车司机决策相关因素的影响机理,综合考虑机场乘客数量的变化规律和出租车司机的收益,建立出租车司机选择决策模型,并给出司机的选择策略。
(2) 收集国内某一机场及其所在城市出租车的相关数据,给出该机场出租车司机的选择方案,并分析模型的合理性和对相关因素的依赖性。
(3) 在某些时候,经常会出现出租车排队载客和乘客排队乘车的情况。某机场“乘车区”现有两条并行车道,管理部门应如何设置“上车点”,并合理安排出租车和乘客,在保证车辆和乘客安全的条件下,使得总的乘车效率最高。
(4) 机场的出租车载客收益与载客的行驶里程有关,乘客的目的地有远有近,出租车司机不能选择乘客和拒载,但允许出租车多次往返载客。管理部门拟对某些短途载客再次返回的出租车给予一定的“优先权”,使得这些出租车的收益尽量均衡,试给出一个可行的“优先”安排方案。
C题解答:本论文来自2019年参赛队伍,最终获得全国一等奖。
摘要
机场作为典型的综合交通枢纽,旅客在下飞机后会有多种交通方式可以选 取,而出租车是主要的陆侧交通工具之一。出租车司机们往往会依据机场的实际情况来选择具体策略,在机场蓄车池排队等待乘客上车或是直接返回市区载客。 本文分别从司机和机场管理部门的角度对实际问题进行研究。
对于问题一,首先分析了影响司机决策的 5 个因素,其中可控因素为泊车位数量、机场距市中心距离和司机平均每小时收益,不可控因素为选择打车的乘客 占比和乘客上车总耗时。在综合考虑司机在机场的排队载客收益 Eairport 和空载返 回市区拉客收益大小 Edowntown 的基础上,建立了出租车司机理性决策模型。同一批到达机场的司机的选择测策略为,若前一辆出租车选择直接离开机场,那么该司机也跟着离开;若前一辆出租车选择进出蓄车池排队等待,则该司机应估算大 致的自己的等待时间Twait 并与等待时间容限T’wait 相比较,在等待时间期望值Twait 小于等待时间容限T’wait 时选择进入蓄车池排队,反之选择离开机场前往市区拉客。
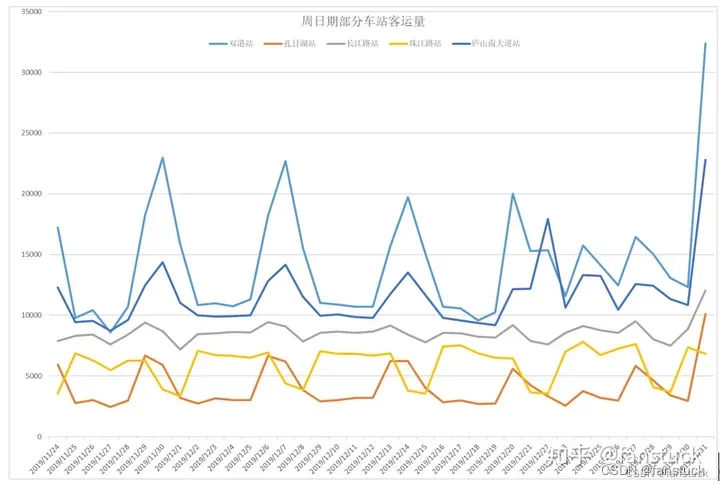
对于问题二,首先通过上海机场有限公司的官网获取了上海浦东机场 2019 年 9 月 13 日的航班数据,并收集了上海市出租车的价位表等信息。在司机理性决策模型的基础上,结合浦东机场的实际数据,用蒙特卡洛算法模拟了该天 22361 辆出租车的实际决策情况。根据仿真结果,当机场开设 5个泊车位时,白 天和夜晚分别有 5219 辆和 8119 辆出租车选择留在机场排队载客(见附表 4)。接着,分别改变机场开放的泊车位数和司机平均每小时收入W0 ,再反复进行多次仿真实验。结果显示,留在机场载客的出租车数与机场开放的泊车位数成正相关,与司机平均每小时的收入成负相关。其中,相对于白天,出租车司机在夜晚 的决策对泊车位数的依赖性更大。
对于问题三,考虑到现实生活中出租车和乘客可能会出现互相等待的情况, 为缓解此现象,本文从修改通行模式和设置泊车位数量的角度来提高乘车效率。分别建立了并行双车道模型和串行单车道模型,并将排队系统每小时的载客数量定义为通行能力Q,以此反映乘车效率。另外,为保证乘客和车辆的安全,需要 考虑泊车位数量增加带来的安全隐患 D。因此,建立了以泊车位数为决策变量, 乘车效率最大化同时安全隐患最小化的双目标优化模型。在求解时,先对通行能力和安全隐患进行归一化处理,再进行等比重加权作为综合得分 S 。求解得,并 行双车道模型和串行单车道模型的泊车位设置分别为 23 和 44时,通行能力最大 值分别是 3431 人/小时和 1293 人/小时,综合得分为 0.6885 和 0.7966。
对于问题四,由于司机的实际收益与载客的行驶里程呈正相关,而乘客的行 驶里程具有很大的随机性。短途出租车与长途出租车的排队时长相似,但收益却相去甚远。为解决该问题,给以短途出租车“短途票”使其享有排队优先权,缓 解出租车司机收入不均衡的问题。建立了以短程阈值 XT 和“短途票”获得上限 NT 为决策变量,司机收益方差最小的优化模型。在求解时,仍然采用蒙特卡洛算法 来对 1000 辆出租车在 10小时内的收益情况进行模拟。求得当短程阈值为 23, “短途票”获得上限为 1 时,出租车司机收入方差最小,为 5688.25。
关键词:理性决策模型 蒙特卡罗模拟 通行能力 双目标优化模型
一、问题重述
1.1 基本情况
机场陆侧交通系统在衔接机场交通和城市交通中发挥着十分重要的作用,出 租车作为一种重要的衔接方式而受到了广泛的研究,本题也需要对机场的出租车接送客系统进行研究。大多数乘客下飞机后要去市区(或周边)的目的地,出租车是主要的交通工具之一。国内多数机场都是将送客(出发)与接客(到达)通道分开的。如果乘客在下飞机后想“打车”,就要到指定的“乘车区”排队,按先后顺序乘车。机场出租车管理人员负责“分批定量”放行出租车进入“乘车区”, 同时安排一定数量的乘客上车。送客到机场的出租车司机都将会面临两个选择:
(1) 前往到达区排队等待载客返回市区。出租车必须到指定的“蓄车池”排队等候,依“先来后到”排队进场载客,等待时间长短取决于排队出租车和乘 客的数量多少,需要付出一定的时间成本。
(2)直接放空返回市区拉客。出租车司机会付出空载费用和可能损失潜在 的载客收益。在某时间段抵达的航班数量和“蓄车池”里已有的车辆数是司机可观测到的 确定信息。司机依据个人的经验对其观测到的数据进行判断,而后作出相应的选择决策。
1.2 问题提出
试就相关情况,建立数学模型,解决如下问题:
(1) 分析研究与出租车司机决策相关因素的影响机理,综合考虑机场乘客数 量的变化规律和出租车司机的收益,建立出租车司机选择决策模型,并给出司机 的选择策略;
(2) 收集国内某一机场及其所在城市出租车的相关数据,给出该机场出租车 司机的选择方案,并分析模型的合理性和对相关因素的依赖性;
(3) 在某些时候,经常会出现出租车排队载客和乘客排队乘车的情况。某机 场“乘车区”现有两条并行车道,给出管理部门设置“上车点”的方案,并合理安排出租车和乘客,在保证车辆和乘客安全的条件下,使得总的乘车效率最高;
(4)机场的出租车载客收益与载客的行驶里程有关,对于短程旅客,出租车 司机不能选择乘客和拒载,但允许出租车多次往返载客。为管理部门制定“优先”安排方案,对某些短途载客再次返回的出租车给予一定的“优先权”,使得这些 出租车的收益尽量均衡。
二、基本假设
为了使研究问题简化,作如下假设:
(1)不考虑天气等因素造成的航班延误、取消等特殊情况,且航班运行情况正常。
(2)各出租车司机的个人经验(即对于航班信息的解读、对于同一时间段内可能打车的乘客数量的判断)大致相同;
(3)司机一旦前往蓄车池排队接客,则不能选择乘客和拒载;
(4)司机一旦进入蓄车池,则不可以再改变决策方案,也即蓄车池单向通 行;
(5)机场建在郊区,距离市中心有一定距离;
(6)各司机由机场开往市区,而后在市区接客之前的距离近似相等;
(7)直接放空返回市区拉客的途中无乘客搭乘出租车;
三、符号说明
四、问题分析
4.1 问题一的分析
问题一首先要求我们探索影响出租车司机决策的相关因素,并且分析其影响 机理。本文罗列出几个确定因素和不确定因素,并分析各自对司机决策的正反作用关系。接着,题目要求建立出租车司机决策模型以研究司机选择策略。依据经济学 中的理论决策模型:假如方案基本是相同的,决策者通常会作相同的决定。理想地,前面队伍中的一个司机选择离开之后,那么队伍后面的司机也全部都会离开,作出同样的选择(去市区拉客),一个司机的想法具有代表性。于是,本问从一 个司机的视角出发,模拟其心理过程以建立相关模型。司机根据经验对两种选择(留在机场拉客和放空返回市区拉客)的收益差作 出判断,而后选择收益大的策略。首先,定性地分析司机收益与损失的正常工作成本和直接收益有关,进一步建立收益子模型,定量地表示出收益。需要求解的难点是队列中司机的等待时间。接着,通过排队等待子模型的建立,将时间离散化,以批为单位考虑乘客和出租车。基于转换后的时间轴,考虑当前司机处于时间轴上的位置、乘客流的到达情况,分析队列中司机的等待时间。最后,综合三 个子模型,得到司机决策的总模型。
4.2 问题二的分析
在问题一模型建立的基础之上,通过查阅资料,获得浦东机场的相关数据,接着我们以上海浦东机场为研究载体来求解该问。对照问题一中对相关因素的影响机理的定性分析,将该问的结果和之作对比,以验证模型的合理性。然后对相关因素进行敏感性分析,敏感程度作为依赖性的刻画指标。
4.3 问题三的分析
问题三要求我们给出管理部门设置“上车点”、以及安排出租车和乘客的方案,这实际上是一个优化问题。依照题意,新的“上车点”设置方案应当满足两个优化目标,即系统乘车效率最大化,同时系统安全隐患最小化,从而得到了双目标优化模型。为了定量描述效率和安全隐患,我们引入通行能力和安全隐患这两个指标。考虑到程序的复杂度和运行时间,通过线性加权将双目标优化问题转化为单目标优化模型以简化程序计算,并将泊车位的个数范围作为约束条件。在机场“乘车区”现有两条并行车道的条件下,综合上车点的设置和泊位区车辆的行驶规则,考虑位置、个数的变化,分析得到设置“上车点”有三种情况。其中两种情况需要我们对之进行优化。
4.4 问题四的分析
考虑到司机的实际收益与载客的行驶里程呈正相关,而乘客的行驶里程具有很大的随机性。短途出租车与长途出租车的排队时长相似,但收益却相去甚远,在低收益的情况下甚至要承担高风险。为解决该问题,给以短途出租车“短途票”使其享有排队优先权,缓解出租车司机收入不均衡的问题。建立了以短程阈值 XT和“短途票”获得上限 NT 为决策变量,司机收益方差最小的优化模型。
五、模型的建立与求解
略(原文太长,涉及公式符号太多,此处不展示。下面为该章节中的部分图表展示)















后续图表略
六、模型评价、改进与推广
6.1 模型的优点
(1)模型全部基于实际模拟仿真机场出租车运行情况,结果更具有客观性。
(2)结果有着很强的可靠性,对每一次仿真都进行大量次数的实验,以消 除随机扰动对结果带来的误差。
(3)在保证程序结果的基础上,以近似公式代替实际模拟公式,很大程度 地缩短程序运行时间,(较之前减少了 2/3)。
(4)模型比较丰富,对具体问题提出多个模型进行分析,并综合考虑多个 模型优缺点,得出最佳方案。
6.2 模型的不足
(1)考虑到本题目没有直接地提供有效数据,并且数据来源受限,所以参 考数据样本空间较小,不利于模型的检验。
(2)模型仅考虑影响决策的主要因素,对于影响较小的因素和某些未知因 素选择忽略。
(3)模型只对一般化的情况进行分析,对于某些特殊的突发情况也不做考 虑。
6.3 模型的推广
模型不仅适用于机场出租车排队载客情况,也可以推广到更一般的大型交通 枢纽车辆调度问题。
七. 参考文献
[1] 姜启源,谢金星,叶俊. 数学模型(第四版). 北京:高等教育出版社,2011.
[2] 孙健,丁日佳,陈艳艳.基于排队论的单车道出租车上客系统建模与仿真[J]. 系统仿真学报,2017,29(05):996-1004.
[3]https://www.shanghaiairport.com/cn/jcjt/index_53191.html
[4] 颜超.上海市枢纽机场陆侧公共交通管理研究[D].华东师范大学,2015.
[5] 官盛飞. 虹桥机场旅客特性调查分析[A].上海空港(第 20 辑)[C].:上海 世纪出版股份有限公司科学技术出版社,2015:7.
[6] Transportation Research Board. Highway capacity manual 2000[M]. Washington D.C.:National Research Council.2000.
[7]吴娇蓉,李铭,梁丽娟.综合客运枢纽出租车上客点管理模式和效率分析[J]. 交通信息与安全,2012,30(04):18-23.
[8]胡稚鸿,董卫,曹流,高忠,陆志勇,吕俊,黄宏标,顾非凡.大型交通枢纽出租车智能匹配管理系统构建与实施[J].创新世界周刊,2019(07):90-95.
附录
程序运行环境:
MATLAB 版本: 12.0.0.341360 (R2020a)
LINGO 版本: 11.0
操作系统:Windows 10
论文写作软件:Word 2019
插图来自:Office-365 Visio / Edraw Max/MATLAB (R2020a)
程序代码和表格(略)文章来源:https://www.toymoban.com/news/detail-634865.html
完整版PDF论文请私信CSDN后台或者添加QQ:2122961493获取文章来源地址https://www.toymoban.com/news/detail-634865.html
到了这里,关于【数学建模】2019 年全国大学生数学建模竞赛C题全国一等奖获奖论文的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!