【LeetCode-中等】221. 最大正方形（详解）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【LeetCode-中等】221. 最大正方形（详解）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

题目

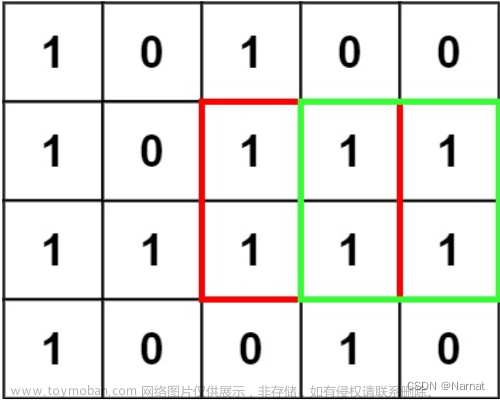
在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

力扣原题链接

寻找最大正方形,LeetCode刷题,leetcode,算法,动态规划

方法1：暴力

暴力法一般不是最优解，但是可以拿来练手

由于正方形的面积等于边长的平方，因此要找到最大正方形的面积，首先需要找到最大正方形的边长，然后计算最大边长的平方即可。

暴力法是最简单直观的做法，具体做法如下：

遍历矩阵中的每个元素，每次遇到 11，则将该元素作为正方形的左上角；

确定正方形的左上角后，根据左上角所在的行和列计算可能的最大正方形的边长（正方形的范围不能超出矩阵的行数和列数），在该边长范围内寻找只包含 11 的最大正方形；

每次在下方新增一行以及在右方新增一列，判断新增的行和列是否满足所有元素都是 11。

class Solution {
    public int maximalSquare(char[][] matrix) {
        int maxSide = 0;
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return maxSide;
        }
        int rows = matrix.length, columns = matrix[0].length;
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < columns; j++) {
                if (matrix[i][j] == '1') {
                    // 遇到一个 1 作为正方形的左上角
                    int side = 1;

                    // 计算可能的最大正方形边长
                    int currentMaxSide = Math.min(rows - i, columns - j);
                    //每次新添加一行一列进行判断是否全是'1'
                    for (int k = 1; k < currentMaxSide; k++) {
                        // 判断新增的一行一列是否均为 1
                        boolean flag = true;
                        //如果 右下角时0，那想新增1行1列 是没戏
                        if (matrix[i + k][j + k] == '0') {
                            break;
                        }
                        //判断i+k那一行是不是全是‘1’,那一行是(i+k，j+0)一直到(i+k，j+k)
                        for (int l = 0; l <= k; l++) {
                            if (matrix[i+k][j+l] == '0'){
                                flag = false;
                                break;
                            }
                        }
                        //判断j+k那一行是不是全是‘1’,那一列是(i+0，j+k)一直到(i+k，j+k)
                        for (int l = 0; l <= k; l++) {
                            if (matrix[i+l][j+k] == '0'){
                                flag = false;
                                break;
                            }
                        }
                        //如果新增的行列都判断完毕，都是true,那就边长+1
                        if (flag){
                            side++;
                        }else break;


                    }
                    maxSide = Math.max(side, maxSide);
                }
            }
        }
        int maxSquare = maxSide * maxSide;
        return maxSquare;
    }
}

效果太差了，2635ms

方法2：动态规划

完全不了解动态规划？

动态规划重要的4个步骤

动态规划，就是利用历史记录，来避免我们的重复计算。而这些历史记录，我们得需要一些变量来保存，一般是用一维数组或者二维数组来保存。下面我们先来讲下做动态规划题很重要的4个步骤

1.定义dp数组

我们会用一个数组，来保存历史数组，假设用一维数组 dp[] 吧。这个时候有一个非常重要的点，就是规定你这个数组元素的含义，例如你的 dp[i] 是代表什么意思？

2.找出递推关系式

动态规划类似于高中数学的数学归纳法，当我们要计算 dp[n] 时，是可以利用 dp[n-1]，dp[n-2]…..dp[1]，来推出 dp[n] 的，也就是可以利用历史数据来推出新的元素值，所以我们要找出数组元素之间的关系式，例如 dp[n] = dp[n-1] + dp[n-2]，这个就是他们的关系式了。

3.找出初始值

找出了递推公式，我们还需要初始值，因为递推公式就是靠前面的值推出后面的值，但总得有个头吧，这个头就是初始值。

4.返回值

最终我们要返回dp数组中的哪个值？根据题目做决定

提示

代码如何排错？将dp数组全部输出看看

对动态规划完全不会的同学可以先去做下面两道动态规划入门题

【LeetCode-简单】509. 斐波那契数（详解）

【LeetCode-简单】70. 爬楼梯（详解）

题目分析

在这道题中，是求面积。如果我们让二维数组中的每一个元素作为一个正方形的右下角，

那么这个正方形的大小：

首先，取决于它自己，它自己是0，那没救了，以它作为右下角的正方形无论怎样边长都是0

其次，如果它本身是1，再观察它的上面、左面、左上的方格，以这三者为右下角的正方形的边长中选择最小的，再+1

这里就体现出了动态规划的思想

1.dp[i][j]:

以(i,j)为正方形的右下角的方格，它参与的正方形的边长最大值

2.递推关系：

右下角的方格如果是0，那就直接dp[i][j] = 0，如果是1，那就判断它的上面、左面、左上三个方向的dp数组的值，得到3者最小的那个，再+1

即： dp[i][j] = min( dp[i-1][j], dp[i-1][j-1], dp[i][j-1] )+1

3.初始值：

如果是左边界或者上边界的方格，那么它作为左下角参与的正方形的最大值只能是1，所以直接dp数组中赋值1

4.返回值：

返回dp数组中最大的那个边长，再边长*边长得出答案

class Solution {
    public int maximalSquare(char[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        int dp[][] = new int[m][n];
        int max = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '0') {
                    dp[i][j] = 0;
                } else {
                    //初始化 左边界和上边界的dp
                    if (i == 0){
                        dp[i][j] = 1;
                    }else if (j == 0){
                        dp[i][j] = 1;
                    }else {
                        dp[i][j] = Math.min(dp[i-1][j],Math.min(dp[i-1][j-1],dp[i][j-1]))+1;
                    }
                }
                max = Math.max(max,dp[i][j]);
            }
        }
        return max*max;
    }
}