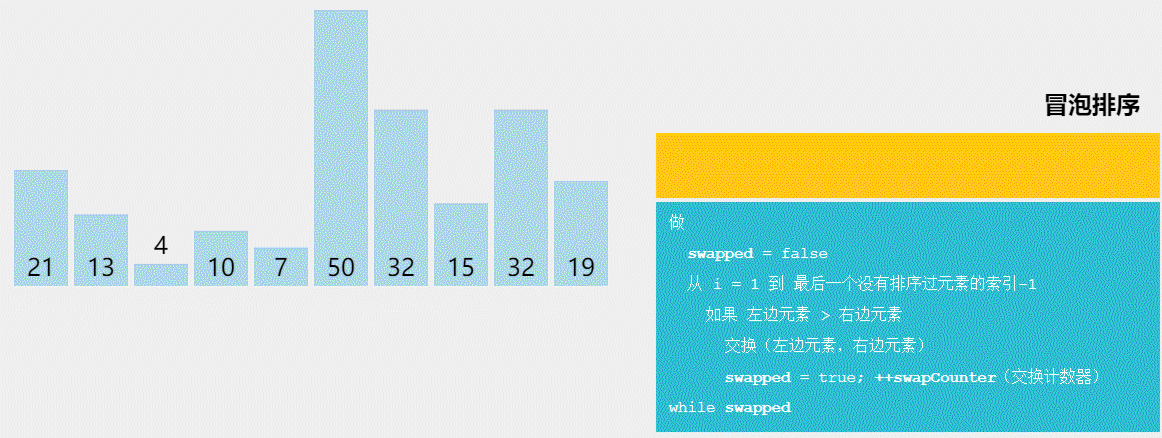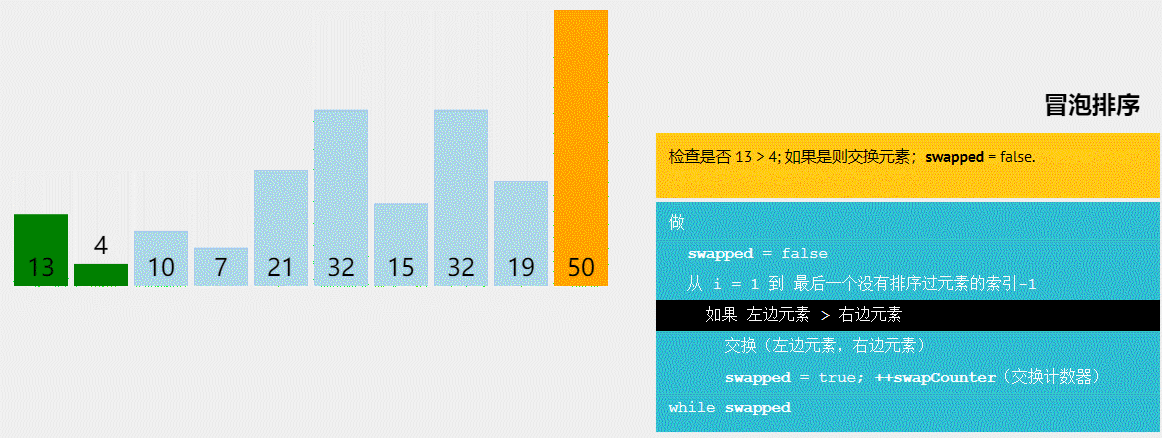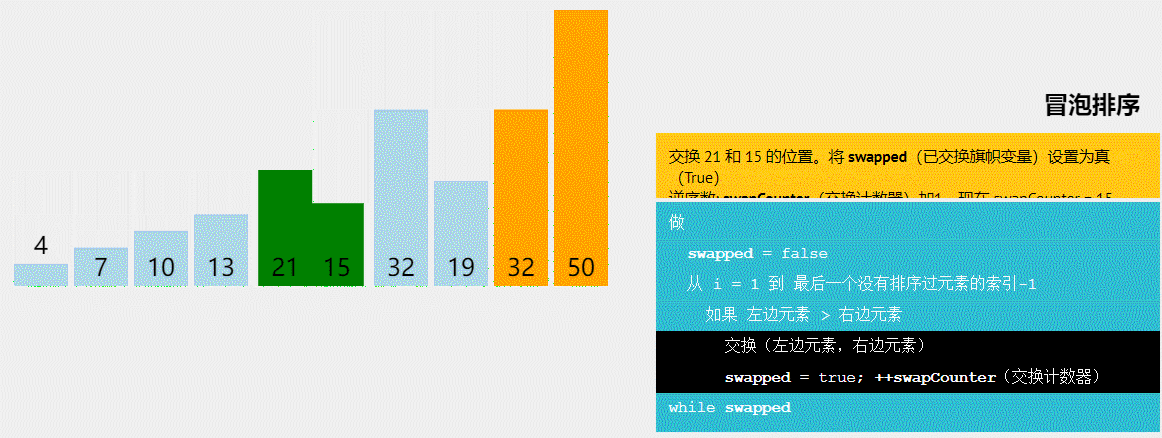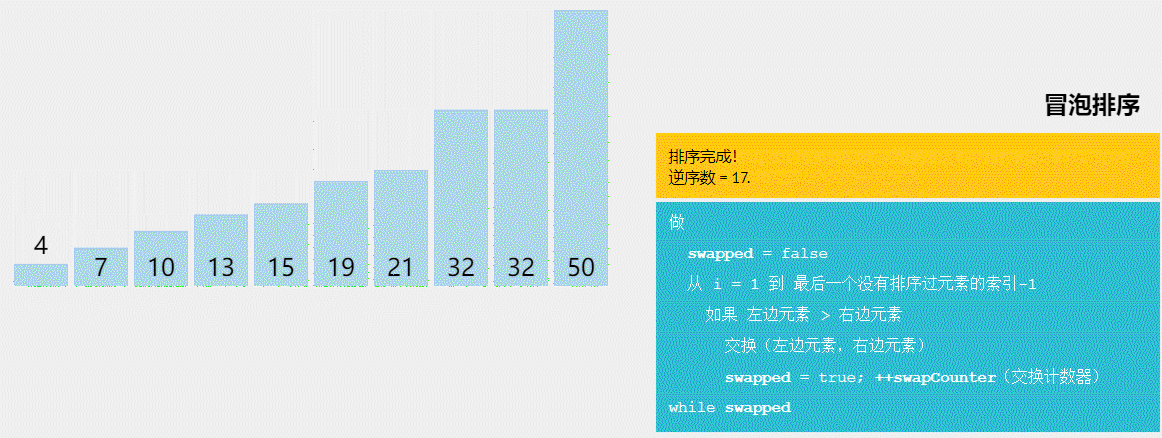排序算法————基数排序（RadixSort）-Toy模板网

这篇具有很好参考价值的文章主要介绍了排序算法————基数排序（RadixSort）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

基数排序的概念：

什么是基数排序？？？基数排序是一种和快排、归并、希尔等等不一样的排序...它不需要比较和移动就可以完成整型的排序。它是时间复杂度是O（K*N），空间复杂度是O（K+M）

基数排序的思想：

基数排序是一种借助多关键字的思想对单逻辑关键字进行排序的方法。

基数排序根据每个位来分配桶，怎么理解呢？？？看下面的动图，0-9就是所分配的桶

用大白话来说，基数排序就是先分发数据再回收数据，可以看看下面的动图。

排序算法————基数排序（RadixSort）,数据结构,排序算法,算法,数据结构

接下来，跟着我的思路走，你也可以实现它。如下面代码，我先定义了一个数组，然后求出来了它的个数。然后就进入基数排序。

int main()
{
	int arr[10] = { 278,109,63,930,589,183,505,269,83,8 };
	int n = sizeof(arr) / sizeof(int);

	for (int i = 0; i < n; i++)
	{
		cout << arr[i] << " ";
	}
	cout << endl;

	//基数排序
	RadixSrot(arr, 0, n);

	for (int i = 0; i < n; i++)
	{
		cout << arr[i] << " ";
	}
	cout << endl;

	return 0;
}

文章来源地址https://www.toymoban.com/news/detail-637005.html

RadixSort函数实现：

思想就是先分发再回收数据。这里的K,我是用宏来定义的，因为我所创建的arr数组最多也就是到了百位，所以其实我们分发3次数据就可以回收了。
#define K 3
void RadixSrot(int arr[],int left,int right) //[left,right)
{
	for (int i = 0; i < K; i++)
	{
		//分发数据
		Distribute(arr, left, right, i);

		//回收数据
		Collect(arr);
	}
}
分发数据的实现：

分发数据中，我用key来接受了每次分发数据后的值。

下面我来演示它每一次的排序情况。

桶其实就是0-9：

0 1 2    3 4 5 6 7 8 9

930    63 505       278 109

183 8 589

83 269

然后第一次排序完就是：930 63 183 83 505 278 8 109 589 269

0 1 2    3 4 5 6 7 8 9

505     930 63 278 183

008 269   083

109 589

第二次排序完就是 505 008 109 930 63 269 278 183 038 589

第三次排序完：8 63 83 109 183 269 278 505 589 930

它的思想就是这样，也因为它是先分发的数据先回收，所以我定义了10个int的队列，因为考虑最坏情况（如果个位数全部是一样的），得到分发过后的个位数后，我就将数字插入到对应的队列中。然后回收，因为是先分发先回收，队列特性刚好满足，就将队列中的数放到数组中，这就完成了第一次的排序。因为都是百位数，所以最多是3次，就用上面的图中的for循环来完成接下里的排序。
#define RADIX 10

//定义基数  构造了10个int的队列
queue<int> Q[RADIX];

void Distribute(int arr[],int left,int right,int k)
{
	
	for (int i = left;i < right; i++)
	{
		int key = GetKey(arr[i], k);
		Q[key].push(arr[i]);
	}

}
int GetKey(int value, int k)
{
	int key = 0;
	while (k >= 0)
	{
		key = value % 10;
		value /= 10;
		k--;
	}

	return key;
}

下面是源码：

#define  _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include <queue>
using namespace std;

#define K 3
#define RADIX 10

//定义基数  构造了10个int的队列
queue<int> Q[RADIX];

//value : 278
//k =0 的时候 就得到8  k=1 就得到7
int GetKey(int value, int k)
{
	int key = 0;
	while (k >= 0)
	{
		key = value % 10;
		value /= 10;
		k--;
	}

	return key;
}

//k代表了第几次分发数据
void Distribute(int arr[],int left,int right,int k)
{
	
	for (int i = left;i < right; i++)
	{
		int key = GetKey(arr[i], k);
		Q[key].push(arr[i]);
	}

}

void Collect(int arr[])
{
	int k = 0;
	for (int i = 0; i < RADIX; i++)
	{
		while (!Q[i].empty())
		{
			arr[k++] = Q[i].front();
			Q[i].pop();
		}
	}
}

void RadixSrot(int arr[],int left,int right) //[left,right)
{
	for (int i = 0; i < K; i++)
	{
		//分发数据
		Distribute(arr, left, right, i);

		//回收数据
		Collect(arr);
	}
}

int main()
{
	int arr[10] = { 278,109,63,930,589,183,505,269,83,8 };
	int n = sizeof(arr) / sizeof(int);

	for (int i = 0; i < n; i++)
	{
		cout << arr[i] << " ";
	}
	cout << endl;

	//基数排序
	RadixSrot(arr, 0, n);

	for (int i = 0; i < n; i++)
	{
		cout << arr[i] << " ";
	}
	cout << endl;

	return 0;
}

到了这里，关于排序算法————基数排序（RadixSort）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！