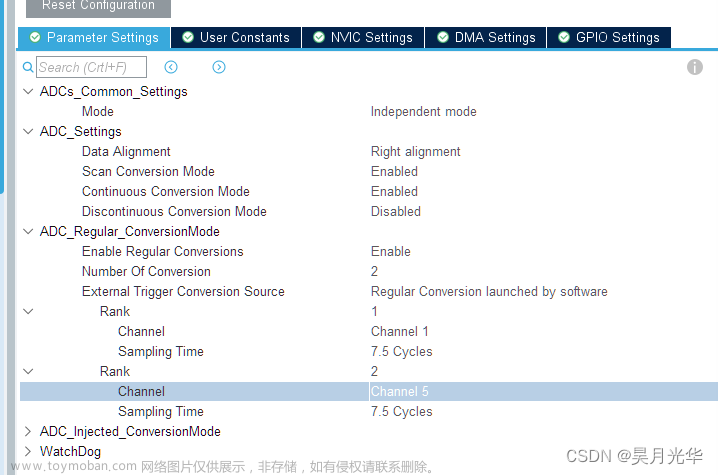
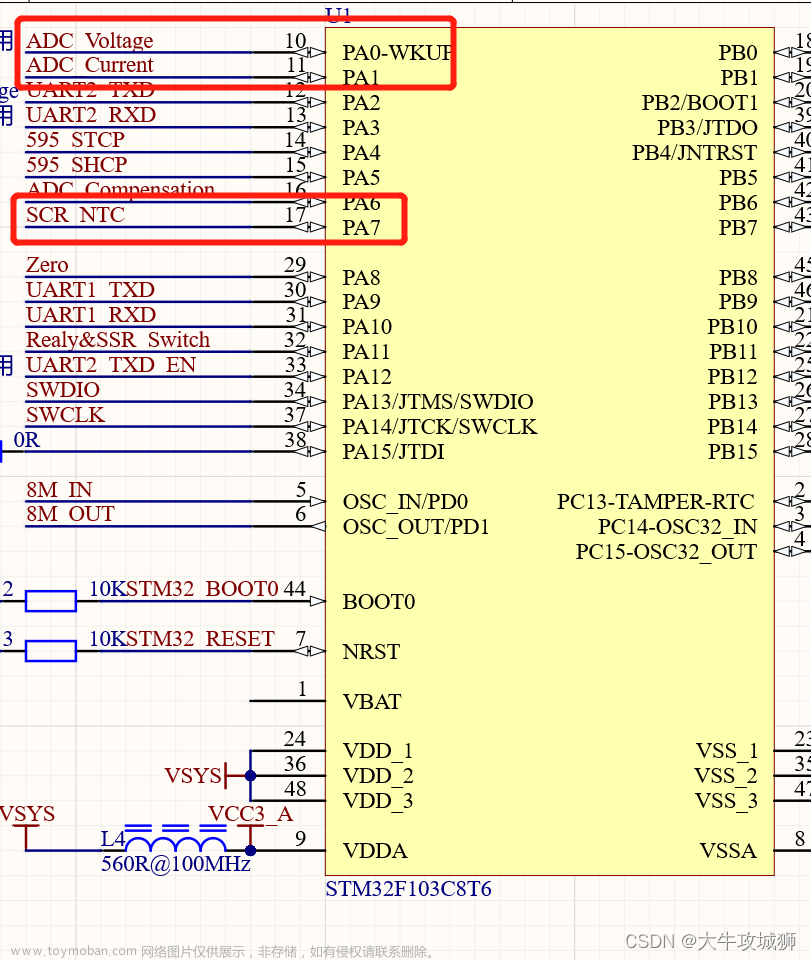
本文主要介绍对ADC采集得到的数字序列进行FFT频谱分析。
确定采样率
确定采样率除了要遵守奈奎斯特采样定律意外还需要考虑一些问题。在数字系统中,我们只能进行一些有限的离散的运算,对于有限长的序列,我们不可能拿它去做DTFT,只能做DFT。这就需要把有限长序列也当作一个周期序列来看待。
归一化角频率
已知采样率为 f s f_s fs,那么一个频率为 f 0 f_0 f0( f 0 < f s / 2 f_0<f_s/2 f0<fs/2)的理想余弦信号被采样后得到的序列应该是:
x [ n ] = A cos ( 2 π f 0 ⋅ n T 0 ) = A cos ( 2 π f 0 ⋅ n f s ) n ∈ Z x[n] = A\cos \left( {2\pi {f_0} \cdot n{T_0} } \right) = A\cos \left( {2\pi {f_0} \cdot {n \over { {f_s} } } } \right)\;\;n \in {\rm{Z} } x[n]=Acos(2πf0⋅nT0)=Acos(2πf0⋅fsn)n∈Z
从上面的式子可以看出,我们实际得到的序列和具体的采样率或信号频率无关,而是由它们俩的比值
f
0
/
f
s
f_0/f_s
f0/fs决定的,就像是信号频率
f
0
f_0
f0被采样频率
f
s
f_s
fs归一化了。
在信号连续的时候,信号的频率
f
f
f可以是任意实数。而在这一离散的情况下,
f
0
/
f
s
f_0/f_s
f0/fs已经将频率限制在了0~1之间,对应到角频率就是0~
2
π
2\pi
2π。
再结合频谱的周期性可以知道
π
\pi
π~
2
π
2\pi
2π的频谱和
−
π
-\pi
−π~
0
0
0的频谱是相同的。
对于一个实序列来说,0~
π
\pi
π的频谱对应频率0~
f
s
/
2
f_s/2
fs/2的复指数序列,而剩下的
π
\pi
π~
2
π
2\pi
2π的频谱则是前者的复共轭。两个互为共轭的复指数序列叠加才构成实序列。根据这一特点,在计算一个实序列的DFT时,可以只算一半的长度,因为另一半只要取复共轭就好了。
有限长序列
前面的分析都是在“理想”的条件下进行了,“理想”指的是这个余弦信号得一直存在,从宇宙诞生之初到遥远的未来始终都存在。这样的信号现实生活中是没有的,实际的信号总有开始和结束。
矩形窗
直接从理想序列中截取几个周期的点构成一个有限长序列,相当于是理想序列在时域上与一个矩形窗相乘,也就是它们在频域的卷积。理想余弦序列的频域的表示已经在上面进行分析了,剩下的只需要关注窗函数的频谱。
计算矩形窗的DTFT,直接用DTFT的分析式:
X ( e j ω ) = ∑ n = 0 N − 1 e j ω n = 1 − e j ω N 1 − e j ω X\left( { {e^{j\omega } } } \right) = \sum\nolimits_{n = 0}^{N - 1} { {e^{j\omega n} } } = { {1 - {e^{j\omega N} } } \over {1 - {e^{j\omega } } } } X(ejω)=∑n=0N−1ejωn=1−ejω1−ejωN
然后可以用下面这个公式进一步化简,
1 − e j 2 θ = 1 − ( cos ( 2 θ ) + j sin ( 2 θ ) ) = − j 2 sin ( θ ) e j θ 1 - {e^{j2\theta } } = 1 - \left( {\cos \left( {2\theta } \right) + j\sin \left( {2\theta } \right)} \right) = - j2\sin \left( \theta \right){e^{j\theta } } 1−ej2θ=1−(cos(2θ)+jsin(2θ))=−j2sin(θ)ejθ
最后得到:
X ( e j ω ) = e − j ω ( N − 1 ) / 2 sin ( ω N / 2 ) sin ( ω / 2 ) X\left( { {e^{j\omega } } } \right) = {e^{ - j\omega (N - 1)/2} }{ {\sin \left( {\omega N/2} \right)} \over {\sin \left( {\omega /2} \right)} } X(ejω)=e−jω(N−1)/2sin(ω/2)sin(ωN/2)
在 ω = 0 \omega=0 ω=0的位置, X ( e j ω ) = 1 X\left( { {e^{j\omega } } } \right) = 1 X(ejω)=1,而在 ω \omega ω是 2 π / N 2\pi/N 2π/N的整数倍时, X ( e j ω ) = 0 X\left( { {e^{j\omega } } } \right)=0 X(ejω)=0。因此当信号的周期正好为 N N N的时候,就不会有频谱泄露(请自行脑补卷积的过程)。
升余弦窗(Hann窗)
升余弦窗也叫Hann窗,可以表示为:
w [ n ] = 1 2 ( 1 − cos ( 2 π n N ) ) , n ∈ [ 0 , N − 1 ] w[n] = {1 \over 2}\left( {1 - \cos \left( {2\pi {n \over N} } \right)} \right),\;\;\;\;n \in \left[ {0,N - 1} \right] w[n]=21(1−cos(2πNn)),n∈[0,N−1]
计算它的DTFT:
X ( e j ω ) = 1 2 ∑ n = 0 N − 1 ( 1 − cos ( 2 π n / N ) ) e − j ω n X\left( { {e^{j\omega } } } \right) = {1 \over 2}\sum\nolimits_{n = 0}^{N - 1} {\left( {1 - \cos \left( {2\pi n/N} \right)} \right){e^{ - j\omega n} } } X(ejω)=21∑n=0N−1(1−cos(2πn/N))e−jωn
我没能显式地求出解,但是可以代入一些特殊值观察一下。当
ω
=
0
\omega=0
ω=0时,
X
(
e
j
ω
)
=
1
/
2
X\left( { {e^{j\omega } } } \right) = 1/2
X(ejω)=1/2,而当
ω
=
±
2
π
/
N
\omega=\pm2\pi/N
ω=±2π/N时,
X
(
e
j
ω
)
=
1
/
4
X\left( { {e^{j\omega } } } \right) = 1/4
X(ejω)=1/4。
X
(
e
j
ω
)
X\left( { {e^{j\omega } } } \right)
X(ejω)与理想序列的频谱卷积得到的结果将会出现频谱泄露。对于单频信号,就会在原来单一的峰值两侧产生两个
1
/
2
1/2
1/2峰值幅度的尖峰,同时峰值幅度也衰减为原来的
1
/
2
1/2
1/2。
虽然称之为“频谱泄露”,但是并不是真的泄露出来,而是由卷积得到的。因此一般情况下直接将泄露的频谱加起来只是一种近似。
不同的窗函数的频谱特性不同,矩形窗的旁瓣比较高,一旦出现频谱泄露就会对特定频率的幅值测量引入很大的误差,但它的频率分辨率也是最高的。Hann窗虽然会有频谱泄露,但它的旁瓣衰减快。
采样率与序列长度
DFT得到的频谱能够分辨的最小频率称为频率分辨力,N点序列做DFT能够得到N点的频谱,因此频率分辨力为 f s / N f_s/N fs/N。最好选取合适的采样率和序列长度使得待测信号的频率正好是频率分辨力的整数倍。如果待测信号的频率正好是频率分辨力的整数倍,那就可以直接用矩形窗;反之,如果待测信号频率不是频率分辨力的整数倍,那就要根据需求加窗。
模拟前端
在确定ADC的采样率之后,ADC前面的抗混叠滤波器的截止频率也要设置在
f
s
/
2
f_s/2
fs/2以内。但也要大于你关心的信号的频率。
采样一些低频的信号一般都是采用这种过采样的方式,ADC前的抗混叠滤波器是低通滤波器,采样率大于信号最高频率的两倍。但采样定理告诉我们只要采样率大于信号带宽的两倍就能恢复采样的信号。所以也有那种带通系统,ADC前用的是带通滤波器,利用数字序列的频谱周期延拓的特性,用低频采样率采高频信号。
仿真信号
在ADC还没调通,或者有时候想自己生成一个单频的仿真序列时,可以直接写出在采样率 f s f_s fs下,频率 f 0 f_0 f0的余弦序列:
x [ n ] = cos ( 2 π f 0 f s n ) x[n] = \cos \left( {2\pi { { {f_0} } \over { {f_s} } }n} \right) x[n]=cos(2πfsf0n)
DSP库函数
在之前的一篇文章中,我提到了用CubeMX生成工程后,在Drivers/CMSIS/Lib目录下就有DSP库文件,所以觉得不用另外从外部导入库DSP库了。
但这两个库文件是有点不同的,我在用CFFT的时候发现只有另外从外部导入的库文件才能正确计算。如果用原来就有的那个库文件,程序在link之后好像有什么奇怪的东西把复位地址的入口给覆盖了,上来就是hardfault。给所以最好还是再另外勾选这个DSP库。
CMSIS的DSP库提供了两种FFT的函数,实数FFT和复数FFT,两者各有特点。都可以用来计算由ADC采样得到的序列的FFT。
实数FFT
实数FFT计算快,是我们的首选!它能够处理长度为32, 64, 128, 256, 512, 1024, 2048, 4096的实数FFT。
输入序列是连续的实数,我之前以为输入也是要和复数FFT一样,实部虚部间隔存放。但实际上它需要的是连续存放的实数。
不是同址运算,输入和输出需要存放在不同地方。输出序列是一个复数序列,长度是输入序列的一半,因为另一半的结果和前一半的结果是互为共轭的关系,不需要重复计算。
而因为复数存放是实部虚部间隔着存放,一个复数占的存储空间是一个实数的两倍。所以输入和输出的实际物理空间占用是一样长的。
比如做1024点浮点数的RFFT,输入是一片长度1024个浮点数的地址空间的首地址,输出也需要同样大小的一篇空间,但是存放的会是512个复数。
输出存放的也不全是复数,一个实数序列
x
[
n
]
x[n]
x[n]做FFT之后得到
X
[
k
]
X[k]
X[k],
X
[
0
]
X[0]
X[0]一定是实数,
X
[
N
/
2
]
X[N/2]
X[N/2]也一定是实数,这两个实数是一起存在第一个复数的位置。
示例代码:
arm_rfft_fast_instance_f32 xInstFFT;
arm_rfft_fast_init_f32(&xInstFFT, 1024);
arm_rfft_fast_f32(&xInstFFT, pSrc, pDst, 0);
在调用RFFT之前,需要先初始化一个实例,主要是设置旋转因子的查找表。RFFT一直都会进行bit reverse,这样输入和输出都是我们习惯的顺序,而CFFT是可以选择是否要bit reverse。arm_rfft_fast_f32中的最后一个参数是选择进行FFT还是IFFT。
复数FFT
#include "arm_const_structs.h"
arm_cfft_f32(arm_cfft_sR_f32_len1024, pData, 0, 1);
复数FFT要求输入的数据就是实部和虚部交替存放的,而且是同址运算,输出结果会覆盖输入的数据。相比于RFFT,它不需要初始化,只需要include arm_const_structs.h这个头文件,就能找到现成的实例。
这个头文件在CMSIS的DSP/Include路径下,虽然我们不能用这里提供的DSP库文件,但是头文件还是能拿来用的。倒数第二个参数是选择进行FFT还是IFFT;最后一个参数是是否需要bit reverse。
Hann窗
Hann窗的系数可以用Matlab计算,可以把这些系数存成常量,方便加窗的时候直接调用。
打开Matlab的窗设计器,选择Hann窗,然后采样选“周期性”。将系数保存到工作区,然后想办法再写到C/C++的源文件里去就好了。文章来源:https://www.toymoban.com/news/detail-637052.html
function [w] = genHann()
w = hann(1024, 'periodic');
end
我是用Matlab Coder把上面这个函数转成C代码,但是也挺麻烦的,感觉还不如直接从工作区复制出来自己写到源文件里去。文章来源地址https://www.toymoban.com/news/detail-637052.html
到了这里,关于基于STM32的ADC采样序列频谱分析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!