算法与数据结构-跳表-Toy模板网

这篇具有很好参考价值的文章主要介绍了算法与数据结构-跳表。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

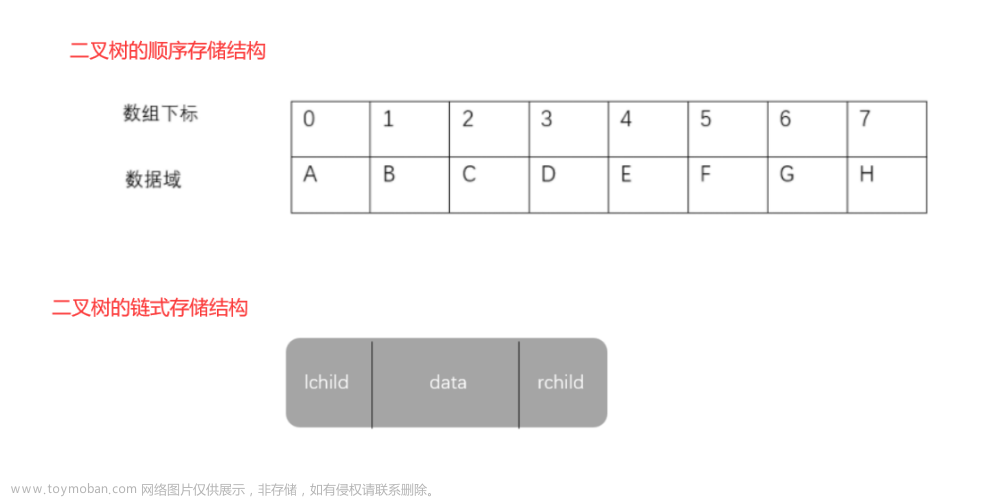
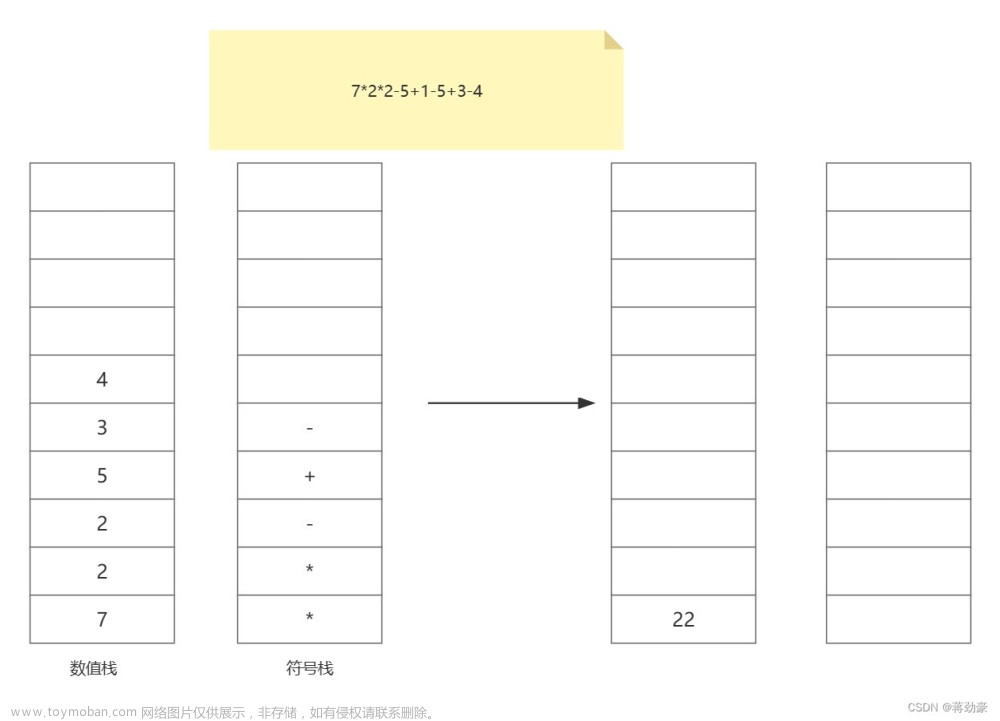
什么是跳表

对于一个单链表来讲，即便链表中存储的数据是有序的，如果我们要想在其中查找某个数据，也只能从头到尾遍历链表。这样查找效率就会很低，时间复杂度会很高，是 O(n)。
算法与数据结构-跳表,算法与数据结构,算法,数据结构
那怎么来提高查找效率呢？如果像图中那样，对链表建立一级“索引”，查找起来是不是就会更快一些呢？每两个结点提取一个结点到上一级，我们把抽出来的那一级叫做索引或索引层。你可以看我画的图。图中的 down 表示 down 指针，指向下一级结点。
算法与数据结构-跳表,算法与数据结构,算法,数据结构
如果我们现在要查找某个结点，比如 16。我们可以先在索引层遍历，当遍历到索引层中值为 13 的结点时，我们发现下一个结点是 17，那要查找的结点 16 肯定就在这两个结点之间。然后我们通过索引层结点的 down 指针，下降到原始链表这一层，继续遍历。这个时候，我们只需要再遍历 2 个结点，就可以找到值等于 16 的这个结点了。这样，原来如果要查找 16，需要遍历 10 个结点，现在只需要遍历 7 个结点。

从这个例子里，我们看出，加来一层索引之后，查找一个结点需要遍历的结点个数减少了，也就是说查找效率提高了。那如果我们再加一级索引呢？效率会不会提升更多呢？

跟前面建立第一级索引的方式相似，我们在第一级索引的基础之上，每两个结点就抽出一个结点到第二级索引。现在我们再来查找 16，只需要遍历 6 个结点了，需要遍历的结点数量又减少了。
算法与数据结构-跳表,算法与数据结构,算法,数据结构
这种链表加多级索引的结构，就是跳表。

跳表的时间复杂度

按照我们刚才讲的，每两个结点会抽出一个结点作为上一级索引的结点，那第一级索引的结点个数大约就是 n/2，第二级索引的结点个数大约就是 n/4，第三级索引的结点个数大约就是 n/8，依次类推，也就是说，第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2，那第 k 级索引结点的个数就是 n/(2^k)。

假设索引有 h 级，最高级的索引有 2 个结点。通过上面的公式，我们可以得到 n/(2^h)=2，从而求得 h=log2n-1。如果包含原始链表这一层，整个跳表的高度就是 log2n。我们在跳表中查询某个数据的时候，如果每一层都要遍历 m 个结点，那在跳表中查询一个数据的时间复杂度就是 O(m*logn)。

那这个 m 的值是多少呢？按照前面这种索引结构，我们每一级索引都最多只需要遍历 3 个结点，也就是说 m=3，为什么是 3 呢？我来解释一下。

假设我们要查找的数据是 x，在第 k 级索引中，我们遍历到 y 结点之后，发现 x 大于 y，小于后面的结点 z，所以我们通过 y 的 down 指针，从第 k 级索引下降到第 k-1 级索引。在第 k-1 级索引中，y 和 z 之间只有 3 个结点（包含 y 和 z），所以，我们在 K-1 级索引中最多只需要遍历 3 个结点，依次类推，每一级索引都最多只需要遍历 3 个结点。

算法与数据结构-跳表,算法与数据结构,算法,数据结构

通过上面的分析，我们得到 m=3，所以在跳表中查询任意数据的时间复杂度就是 O(logn)。这个查找的时间复杂度跟二分查找是一样的。换句话说，我们其实是基于单链表实现了二分查找.

跳表的空间复杂度

通过上面的分析，我们得到 m=3，所以在跳表中查询任意数据的时间复杂度就是 O(logn)。这个查找的时间复杂度跟二分查找是一样的。换句话说，我们其实是基于单链表实现了二分查找

算法与数据结构-跳表,算法与数据结构,算法,数据结构
这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以，跳表的空间复杂度是 O(n)。也就是说，如果将包含 n 个结点的单链表构造成跳表，我们需要额外再用接近 n 个结点的存储空间。

如何高效的插入和删除

我们知道，在单链表中，一旦定位好要插入的位置，插入结点的时间复杂度是很低的，就是 O(1)。但是，这里为了保证原始链表中数据的有序性，我们需要先找到要插入的位置，这个查找操作就会比较耗时。

对于纯粹的单链表，需要遍历每个结点，来找到插入的位置。但是，对于跳表来说，我们讲过查找某个结点的时间复杂度是 O(logn)，所以这里查找某个数据应该插入的位置，方法也是类似的，时间复杂度也是 O(logn)。我画了一张图，你可以很清晰地看到插入的过程。

算法与数据结构-跳表,算法与数据结构,算法,数据结构

我们再看下删除操作。如果这个结点在索引中也有出现，我们除了要删除原始链表中的结点，还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点，然后通过指针操作完成删除。所以在查找要删除的结点的时候，一定要获取前驱结点。当然，如果我们用的是双向链表，就不需要考虑这个问题了。

跳表索引动态更新

当我们不停地往跳表中插入数据时，如果我们不更新索引，就有可能出现某 2 个索引结点之间数据非常多的情况。极端情况下，跳表还会退化成单链表。
算法与数据结构-跳表,算法与数据结构,算法,数据结构
作为一种动态数据结构，我们需要某种手段来维护索引与原始链表大小之间的平衡，也就是说，如果链表中结点多了，索引结点就相应地增加一些，避免复杂度退化，以及查找、插入、删除操作性能下降。

当我们往跳表中插入数据的时候，我们可以选择同时将这个数据插入到部分索引层中。如何选择加入哪些索引层呢？

我们通过一个随机函数，来决定将这个结点插入到哪几级索引中，比如随机函数生成了值 K，那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。

算法与数据结构-跳表,算法与数据结构,算法,数据结构
随机函数的选择很有讲究，从概率上来讲，能够保证跳表的索引大小和数据大小平衡性，不至于性能过度退化。文章来源地址https://www.toymoban.com/news/detail-637488.html

代码示例

public class SkipList {

    private static final float SKIPLIST_P = 0.5f;
    private static final int MAX_LEVEL = 16;

    private int levelCount = 1;

    private Node head = new Node();  // 带头链表

    public Node find(int value) {
        Node p = head;
        for (int i = levelCount - 1; i >= 0; --i) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
        }

        if (p.forwards[0] != null && p.forwards[0].data == value) {
            return p.forwards[0];
        } else {
            return null;
        }
    }

    public void insert(int value) {
        // 随机索引层数
        int level = randomLevel();

        // 定义新节点
        Node newNode = new Node();
        newNode.data = value;

        //
        Node update[] = new Node[level];
        for (int i = 0; i < level; ++i) {
            update[i] = head;
        }

        // record every level largest value which smaller than insert value in update[]
        Node p = head;
        for (int i = level - 1; i >= 0; --i) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
            update[i] = p;// use update save node in search path
        }

        // in search path node next node become new node forwords(next)
        for (int i = 0; i < level; ++i) {
            newNode.forwards[i] = update[i].forwards[i];
            update[i].forwards[i] = newNode;
        }

        // update node hight
        if (levelCount < level) levelCount = level;
    }

    public void delete(int value) {
        Node[] update = new Node[levelCount];
        Node p = head;
        for (int i = levelCount - 1; i >= 0; --i) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
            update[i] = p;
        }

        if (p.forwards[0] != null && p.forwards[0].data == value) {
            for (int i = levelCount - 1; i >= 0; --i) {
                if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {
                    update[i].forwards[i] = update[i].forwards[i].forwards[i];
                }
            }
        }

        while (levelCount > 1 && head.forwards[levelCount] == null) {
            levelCount--;
        }

    }

    // 理论来讲，一级索引中元素个数应该占原始数据的 50%，二级索引中元素个数占 25%，三级索引12.5% ，一直到最顶层。
    // 因为这里每一层的晋升概率是 50%。对于每一个新插入的节点，都需要调用 randomLevel 生成一个合理的层数。
    // 该 randomLevel 方法会随机生成 1~MAX_LEVEL 之间的数，且 ：
    //        50%的概率返回 1
    //        25%的概率返回 2
    //      12.5%的概率返回 3 ...
    private int randomLevel() {
        int level = 1;

        while (Math.random() < SKIPLIST_P && level < MAX_LEVEL)
            level += 1;
        return level;
    }

    public void printAll() {
        Node p = head;
        while (p.forwards[0] != null) {
            System.out.print(p.forwards[0] + " ");
            p = p.forwards[0];
        }
        System.out.println();
    }

    public class Node {
        private int data = -1;
        private Node forwards[] = new Node[MAX_LEVEL];
    }
}